
1 离散型随机变量
离散型随机变量 1

随机变量 2 在实际问题中,随机试验的结果可以用数值来表示, 由此产生了随机变量的概念 。 有些试验结果本身与数值有关,因此可用一个变量 来表示试验的各种结果; 口抛一枚骰子出现的点数; ▣ 任取10个产品中的次品数 有些试验结果与数值无关,但可以把结果数值化, 即引入一个变量来表示试验的各种结果 口抛一枚硬币,正面向上用1表示,反面向上用0表示 口 课上任选一名同学,用其学号表示 口火箭返回地球的落点位置可以用坐标或经纬度表示
随机变量 在实际问题中,随机试验的结果可以用数值来表示, 由此产生了随机变量的概念。 有些试验结果本身与数值有关,因此可用一个变量 来表示试验的各种结果; 抛一枚骰子出现的点数; 任取10个产品中的次品数 有些试验结果与数值无关,但可以把结果数值化, 即引入一个变量来表示试验的各种结果 抛一枚硬币,正面向上用1表示,反面向上用0表示 课上任选一名同学,用其学号表示 火箭返回地球的落点位置可以用坐标或经纬度表示 2
随机变量的定义 3 0 我们可以把2中的每一个样本点ω与一个实数 X(ω)相对应,X(ω)可看成ω的实值函数 R 2 Xω) 口称实值函数X:2→R为随机变量(random variable)),简记为r.v
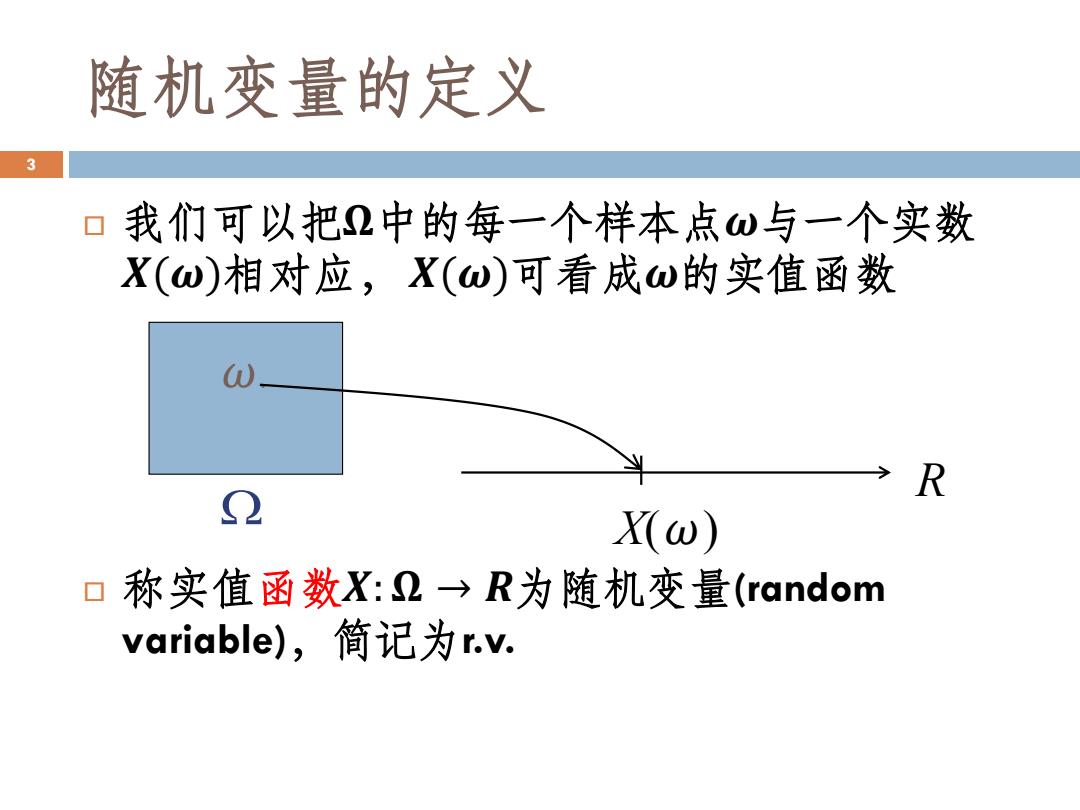
随机变量的定义 我们可以把𝛀中的每一个样本点𝝎与一个实数 𝑿(𝝎)相对应, 𝑿(𝝎)可看成𝝎的实值函数 称实值函数𝑿:𝛀 → 𝑹为随机变量(random variable),简记为r.v. 3 𝜔. X(𝜔) R

随机变量的特点 4 它随试验结果的不同而取不同的值,因而取值 具有随机性。在试验之前只知道它可能取值的 范围,而不能预先确定取哪个值。 由于试验结果的出现具有一定的概率,因此随 机变量取某个值或者某个范围内的值也有一定 的概率。 随机变量在某范围的取值表示随机事件
随机变量的特点 它随试验结果的不同而取不同的值,因而取值 具有随机性。在试验之前只知道它可能取值的 范围,而不能预先确定取哪个值。 由于试验结果的出现具有一定的概率,因此随 机变量取某个值或者某个范围内的值也有一定 的概率。 4 随机变量在某范围的取值表示随机事件

例 5 口抛一枚骰子,令X=出现的点数,则X是一v. 口X的取值为1,2,3,4,5,6 ▣{X≤4}表示事件:点数不超过4 口{X为偶数}表示事件:点数为偶数 0】 观察某电子元件的寿命,令Z:该元件的寿命, 则Z是一v. 口Z的取值为所有非负实数 ▣{Z≤500}表示事件:该元件寿命不超过500h
例 抛一枚骰子,令𝑿 =出现的点数,则𝑿是一r.v. 𝑿的取值为1,2,3,4,5,6 {𝑿 ≤ 𝟒}表示事件:点数不超过4 {𝑿为偶数}表示事件:点数为偶数 观察某电子元件的寿命,令𝒁:该元件的寿命, 则𝒁是一r.v. 𝒁的取值为所有非负实数 {𝒁 ≤ 𝟓𝟎𝟎}表示事件:该元件寿命不超过500h 5

随机变量的意义 6 口引入随机变量后,可以利用随机变量来描述随 机现象,对事件及事件概率的研究扩大为对随 机变量及其取值规律的研究。 ▣有了随机变量,可以使用更多的数学工具
随机变量的意义 引入随机变量后,可以利用随机变量来描述随 机现象,对事件及事件概率的研究扩大为对随 机变量及其取值规律的研究。 有了随机变量,可以使用更多的数学工具。 6

随机变量的分类 通常分为两类: 口离散型随机变量:所有可能取值可以一一列举 口例:取到次品的个数,抛骰子的点数 连续型随机变量:所有取值不可一一列举,可 取一个区间内的所有值 口例:元件的寿命,到达车站的时刻
随机变量的分类 通常分为两类: 离散型随机变量:所有可能取值可以一一列举 例:取到次品的个数,抛骰子的点数 连续型随机变量:所有取值不可一一列举,可 取一个区间内的所有值 例:元件的寿命,到达车站的时刻 7

离散型随机变量 8 若随机变量X的取值是有限个或者可列无穷个, 则称X为离散型随机变量。 口设离散型随机变量X的所有可能取值为 X1,X2,…,X… 并设P(X=xn)=pn(n=1,2,…), 则称上式为X的分布律,常表示为 X X1 X2 Xn P P P2 Pn
离散型随机变量 若随机变量𝑿的取值是有限个或者可列无穷个, 则称𝑿为离散型随机变量。 设离散型随机变量𝑿的所有可能取值为 𝒙𝟏, 𝒙𝟐, …, 𝒙𝒏, … 并设𝑷(𝑿 = 𝒙𝒏) = 𝒑𝒏 𝒏 = 𝟏, 𝟐, … , 则称上式为𝑿的分布律,常表示为 8 X 1 x 2 x , n x P p1 p2 , pn

离散型随机变量分布律的性质 口对任意的自然数n,有pn≥0 o∑npn=1 例:设随机变量X的分布律为 P(X=n))=4n,n=1,2,… 求常数c 解:据分布律性质知 1-∑Pw=w=∑东黄 故c=3
离散型随机变量分布律的性质 对任意的自然数𝒏,有𝒑𝒏 ≥ 𝟎 σ𝒏 𝒑𝒏 = 𝟏 例:设随机变量𝑿的分布律为 𝑷(𝑿 = 𝒏) = 𝒄 𝟒 𝒏 ,𝒏 = 𝟏, 𝟐, … 求常数𝒄. 解:据分布律性质知 𝟏 = 𝒏 𝑷(𝑿 = 𝒏) = 𝒏 𝒄 𝟒 𝒏 = 𝒄 𝟑 故𝒄 = 𝟑. 9

例 10 0 假设姚明罚球的命中率为0.9,求他两次独立罚 球命中次数X的分布律。 解:X的取值为0,1,2. P(X=0)=(1-0.9)×(1-0.9)=0.01 P(X=1)=2×0.9×(1-0.9)=0.18 P(X=2)=0.9×0.9=0.81 X 0 1 2 P 0.01 0.18 0.81
例 假设姚明罚球的命中率为0.9,求他两次独立罚 球命中次数𝑿的分布律。 解:𝑿的取值为0,1,2. 𝑷 𝑿 = 𝟎 = 𝟏 − 𝟎. 𝟗 × 𝟏 − 𝟎.𝟗 = 𝟎. 𝟎𝟏 𝑷 𝑿 = 𝟏 = 𝟐 × 𝟎. 𝟗 × 𝟏 − 𝟎. 𝟗 = 𝟎.𝟏𝟖 𝑷 𝑿 = 𝟐 = 𝟎. 𝟗 × 𝟎.𝟗 = 𝟎. 𝟖𝟏 10