
1 连续型随机变量
连续型随机变量 1

分布函数 2 口随机变量的取值表示随机事件。 口如:X=π,X<3,0≤X<5都表示随机事件 口对某个实数x,X≤x可以表示随机事件,其概率 P(X≤x)与实数x有关,对每个实数x,都有唯 一的概率值P(X≤x)与之对应,从而构成函数 关系,记为 F(x)=P(X≤x)
分布函数 随机变量的取值表示随机事件。 如:𝑿 = 𝝅,𝑿 < 𝟑,𝟎 ≤ 𝑿 < 𝟓都表示随机事件 对某个实数𝒙,𝑿 ≤ 𝒙可以表示随机事件,其概率 𝑷(𝑿 ≤ 𝒙)与实数𝒙有关,对每个实数𝒙,都有唯 一的概率值𝑷(𝑿 ≤ 𝒙)与之对应,从而构成函数 关系,记为 𝑭 𝒙 = 𝑷(𝑿 ≤ 𝒙) 2
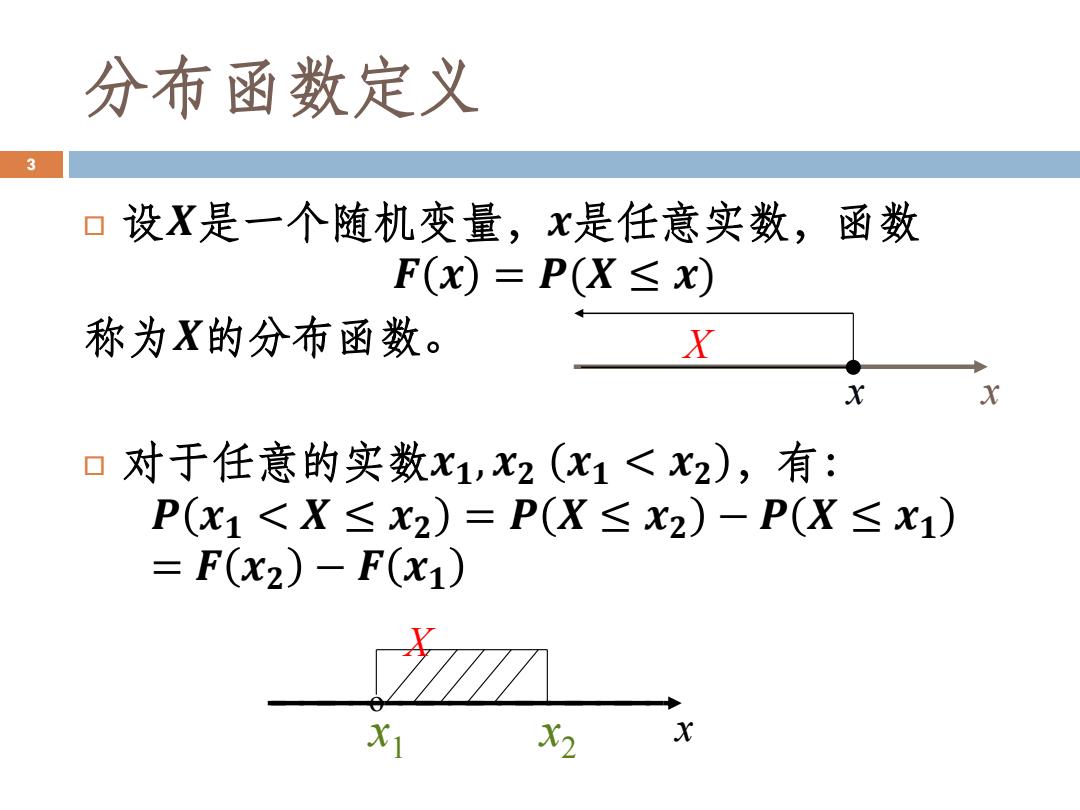
分布函数定义 3 口设X是一个随机变量,x是任意实数,函数 F(x)=P(X≤X) 称为X的分布函数。 X X X 0 对于任意的实数x1,x2(x1<x2),有: P(x1<X≤X2)=P(X≤x2)-P(X≤X1) =F(x2)-F(x1) X1 X2 X
分布函数定义 设𝑿是一个随机变量,𝒙是任意实数,函数 𝑭 𝒙 = 𝑷(𝑿 ≤ 𝒙) 称为𝑿的分布函数。 对于任意的实数𝒙𝟏, 𝒙𝟐 𝒙𝟏 < 𝒙𝟐 ,有: 𝑷 𝒙𝟏 < 𝑿 ≤ 𝒙𝟐 = 𝑷 𝑿 ≤ 𝒙𝟐 − 𝑷 𝑿 ≤ 𝒙𝟏 = 𝑭 𝒙𝟐 − 𝑭 𝒙𝟏 3 x x X x1 x2 x X o
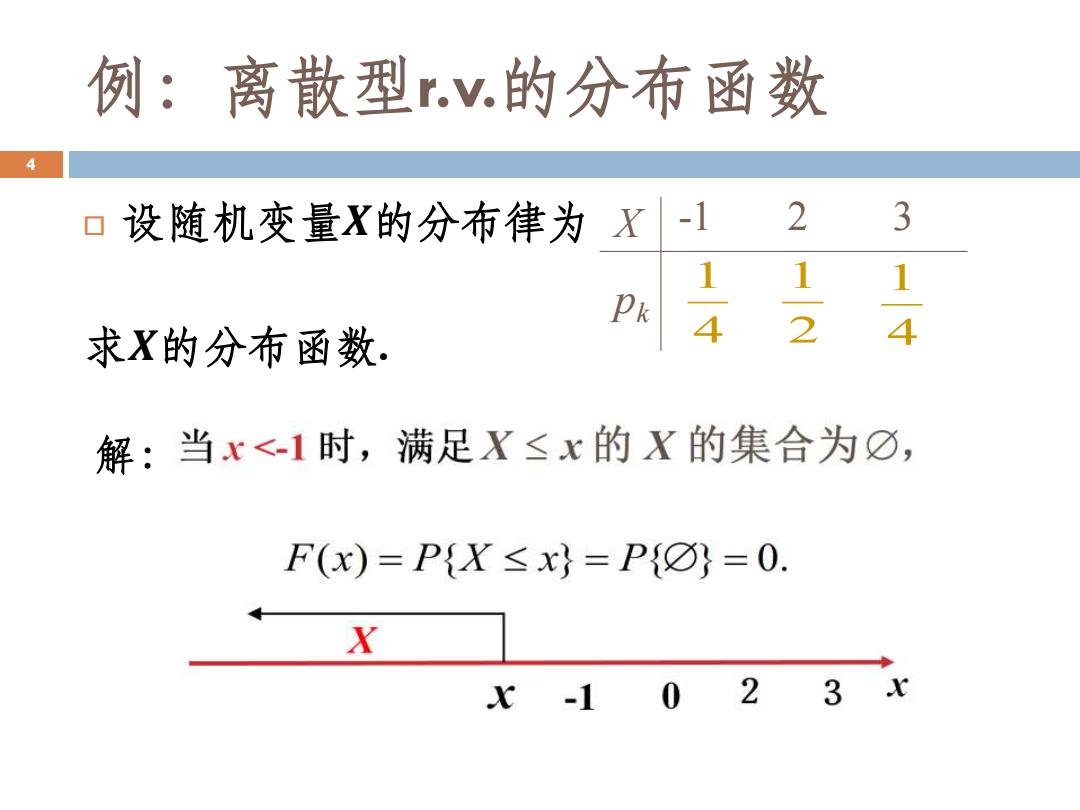
例:离散型v.的分布函数 4 口设随机变量X的分布律为X-1 2 3 1 1 Pk 求X的分布函数. 4 2 4 解:当x<1时,满足X≤x的X的集合为O, F(x)=P{X≤x}=P{O}=0. X x-10 2 3 x
例:离散型r.v.的分布函数 设随机变量𝑿的分布律为 求𝑿的分布函数. 4 X pk 2 1 -1 2 3 4 1 4 1 解:
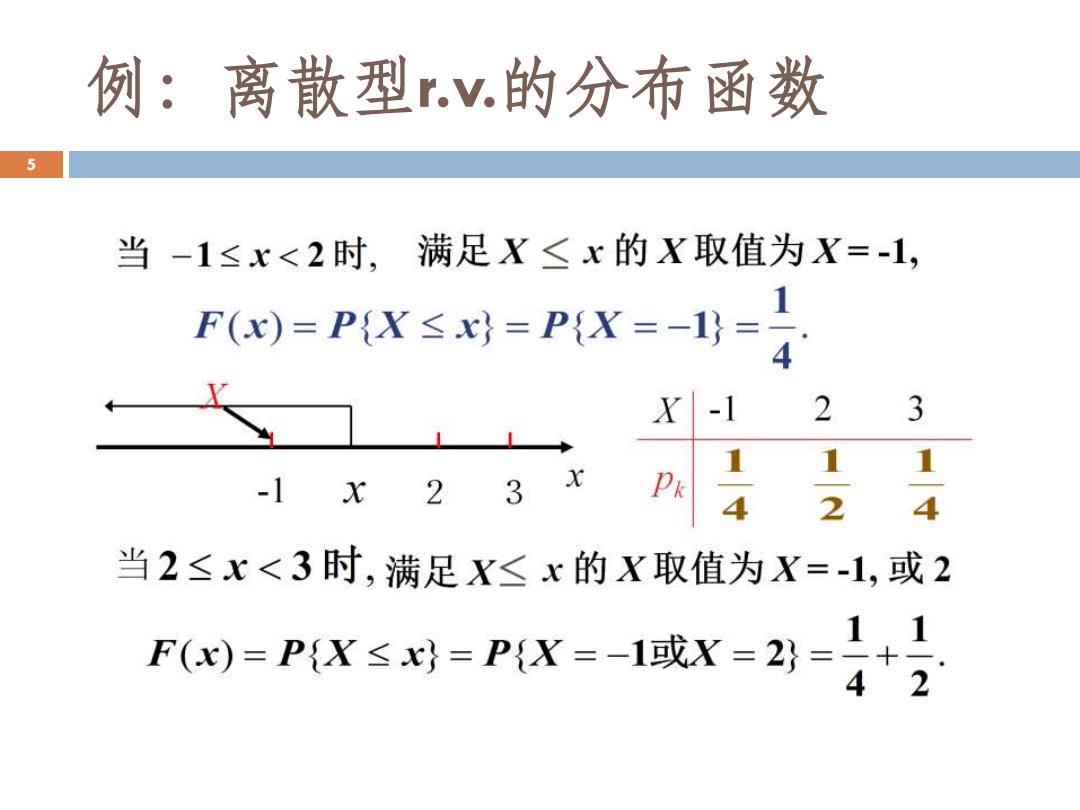
例:离散型v.的分布函数 5 当-1≤x<2时,满足X≤x的X取值为X=-1, FN)=PX≤x=PX=-1=4 X -1 2 3 1 1 1 -1X2 3 Pk 4 2 4 当2≤x<3时,满足X≤x的X取值为X=-1,或2 7()=PX≤g=PX=-1或X=23=+号
例:离散型r.v.的分布函数 5
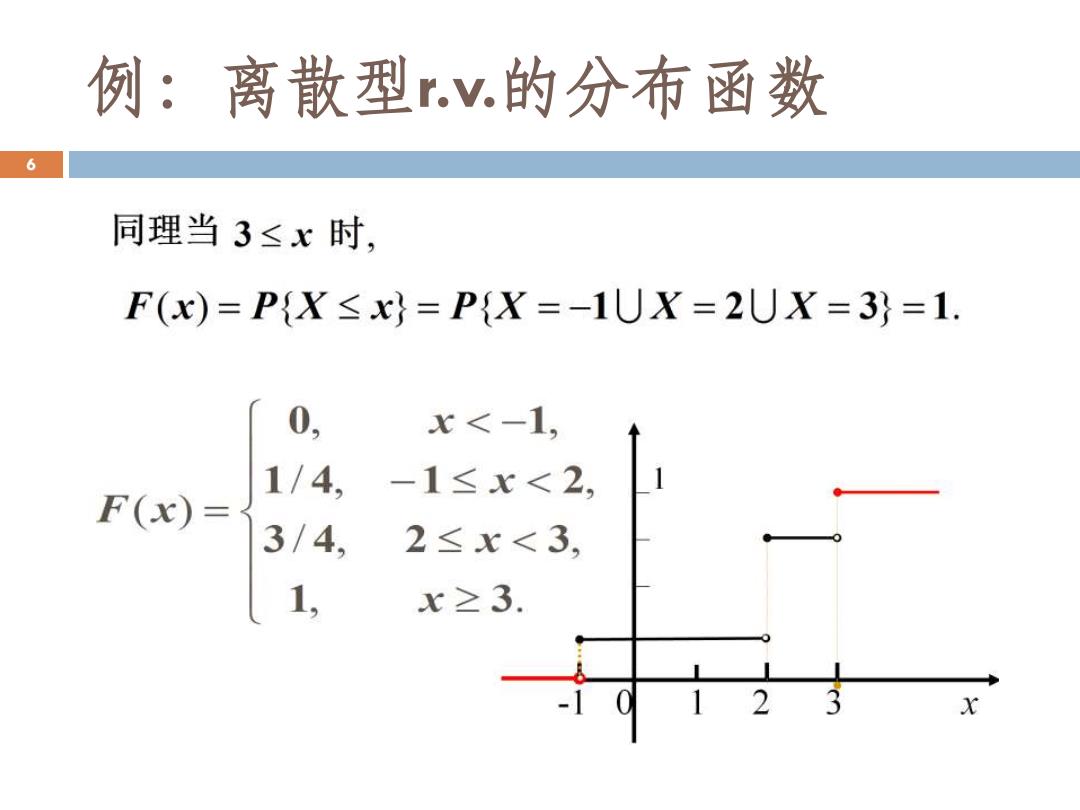
例:离散型rv.的分布函数 6 同理当3≤x时, F(x)=PX<x)=PX=-1UX=2UX=3)=1. 0, x<-1, 1/4, -1≤x<2 F(x)= 3/4. 2≤x<3, 1, x≥3
例:离散型r.v.的分布函数 6
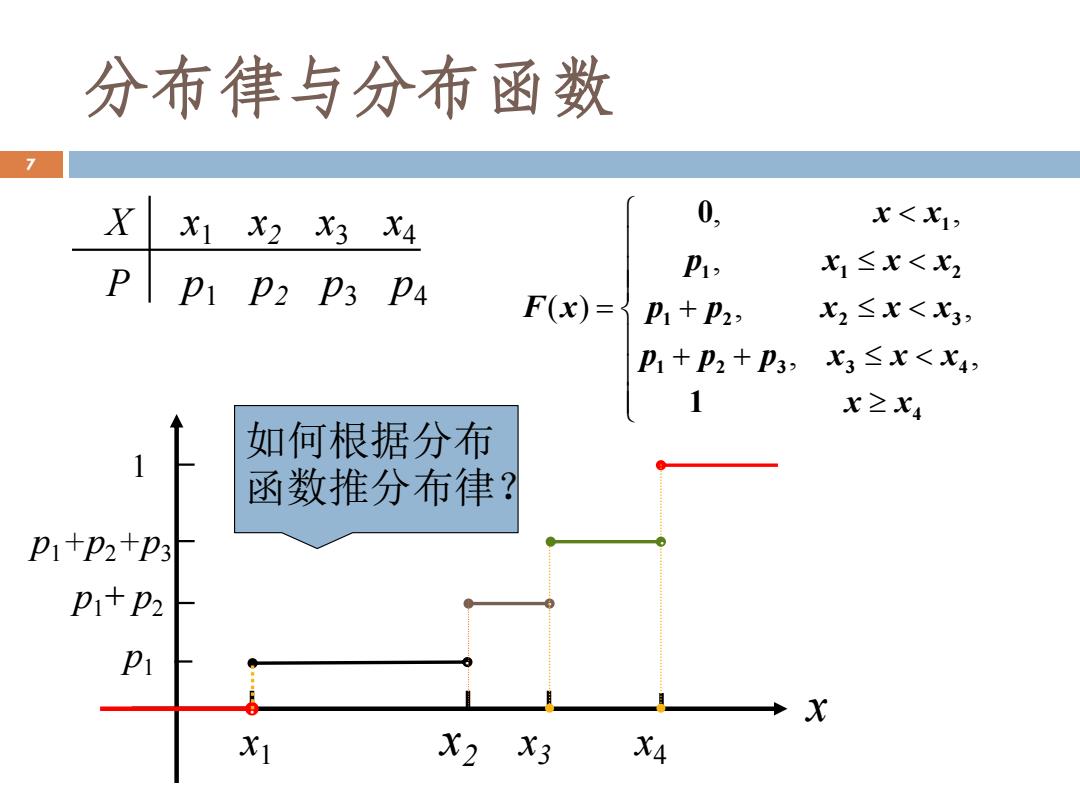
分布律与分布函数 7 X X1 X2 X3 X4 0, X<X1, Pp P2 P3 P4 P1, X1≤x<x2 F(x)=了p1+P2, X2≤x<x3, P1+P2+P3,X3≤x<x4, X≥x4 如何根据分布 函数推分布律? p1+P2+P3 P1+P2 P X X1 X2 X3 XA
分布律与分布函数 7 X x1 x2 x3 x4 P p1 p2 p3 p4 x x1 x2 x3 x4 1 . p . 1 p . 1+ p2 . p1+p2+p3 + + + = 4 1 2 3 3 4 1 2 2 3 1 1 2 1 1 0 x x p p p x x x p p x x x p x x x x x F x , , , , , , , ( ) 如何根据分布 函数推分布律?
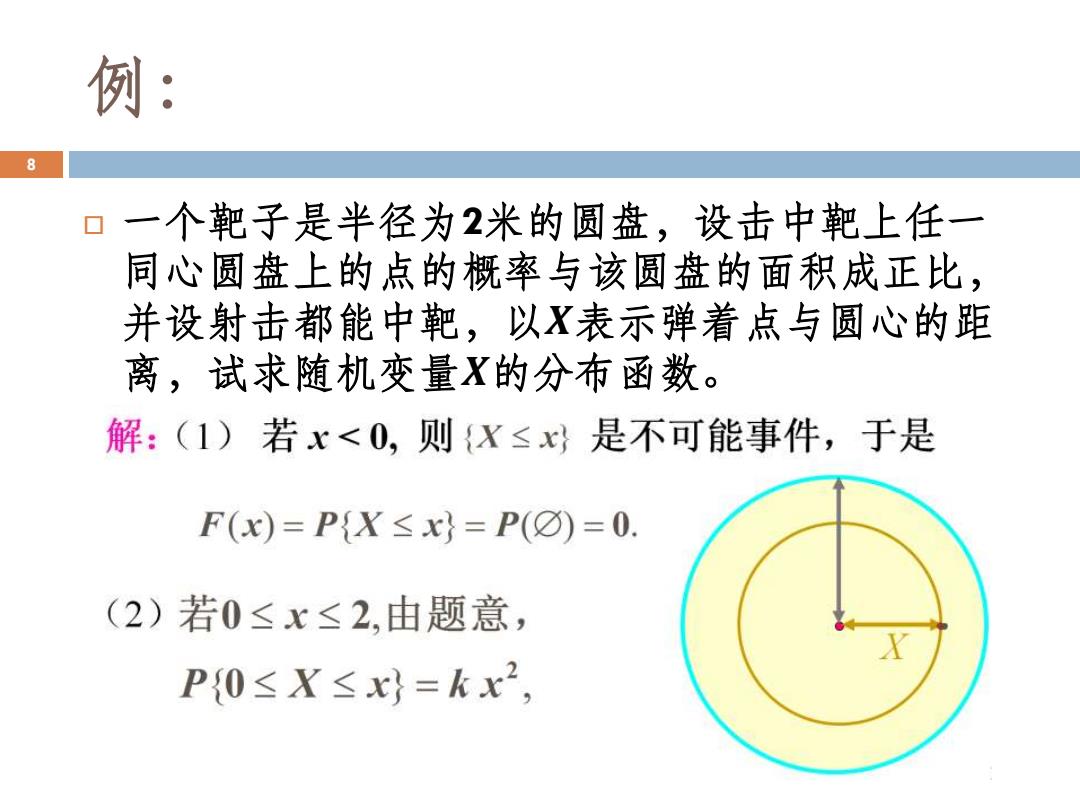
例: 8 一个靶子是半径为2米的圆盘,设击中靶上任一 同心圆盘上的点的概率与该圆盘的面积成正比, 并设射击都能中靶,以X表示弹着点与圆心的距 离,试求随机变量X的分布函数。 解:(1)若x<0,则{X≤x是不可能事件,于是 F(x)=P{X≤x}=P(☑)=0 (2)若0≤x≤2,由题意, P{0≤X≤x}=kx2
例: 一个靶子是半径为2米的圆盘,设击中靶上任一 同心圆盘上的点的概率与该圆盘的面积成正比, 并设射击都能中靶,以𝑿表示弹着点与圆心的距 离,试求随机变量𝑿的分布函数。 8

9 取x=2,由已知得P0≤X≤2}=1,与上式对比 得k=1/4,即P{0≤X≤x}= 4 于是,0≤x≤2时 F(X)=P{X≤x}=P{X<O}+P{0≤X≤x}= 4 (3)若x≥2,则{X≤x}是必然事件,于是 F(x)=P{X≤x}=1
9
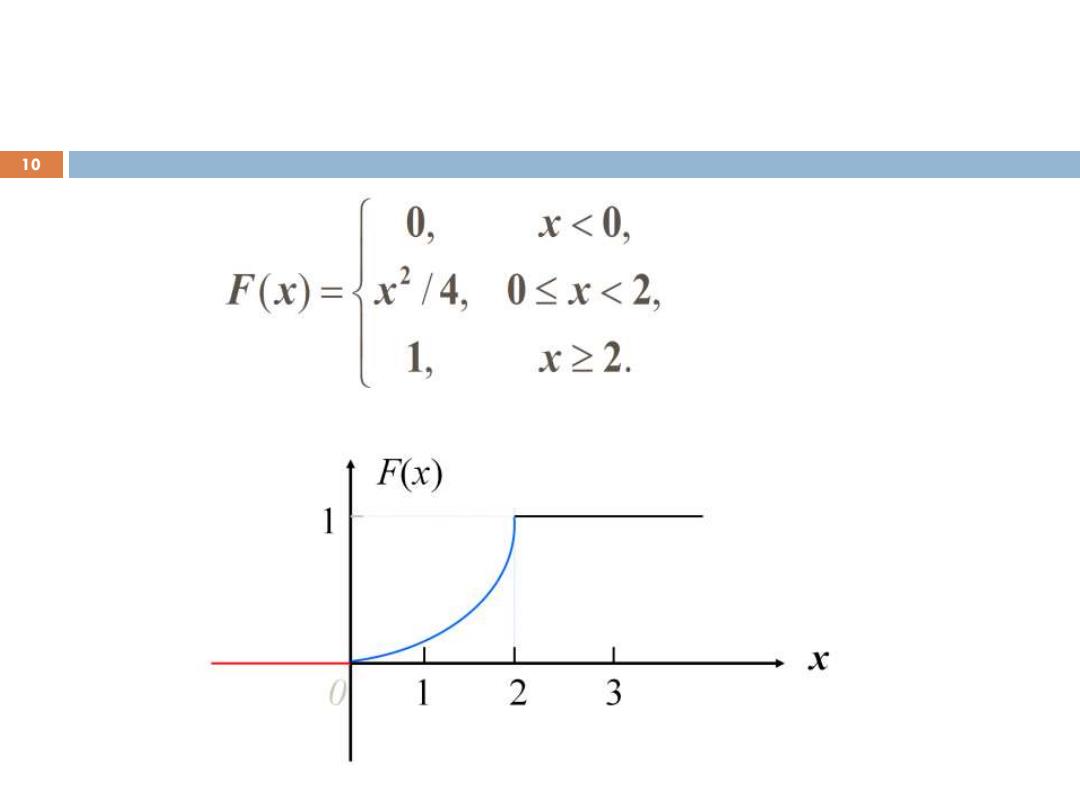
10 0, x<0, F(x)={x2/4,0≤x<2, 1 x≥2. F(x) 1 X 1 2 3
10