
1 典型二维连续型随机 变量分布、相关系数
典型二维连续型随机 变量分布、相关系数 1

二维均匀分布 2 口设D是平面上的有界区域,其面积为A,如果二 维随机变量(X,Y)的密度函数为 px,y=层(xweD (0,(x,y)年D 则称(X,Y)服从D上的二维均匀分布
二维均匀分布 设𝑫是平面上的有界区域,其面积为𝑨,如果二 维随机变量(𝑿,𝒀)的密度函数为 𝒑 𝒙, 𝒚 = ൞ 𝟏 𝑨 , 𝒙, 𝒚 ∈ 𝑫 𝟎, 𝒙, 𝒚 ∉ 𝑫 则称(𝑿, 𝒀)服从𝑫上的二维均匀分布。 2

二维均匀分布背景 3 在平面区域D内随机投点,落点坐标(X,Y),则 (X,Y)服从区域D上的二维均匀分布。 甲乙在一小时内随机达到车站,到达时刻分别 为X,Y,则(X,Y)服从区域D上的二维均匀分布, 其中D={(x,y)川0<x<60,0<y<60}
二维均匀分布背景 在平面区域𝑫内随机投点,落点坐标(𝑿,𝒀),则 (𝑿,𝒀)服从区域𝑫上的二维均匀分布。 甲乙在一小时内随机达到车站,到达时刻分别 为𝑿, 𝒀,则(𝑿, 𝒀)服从区域𝑫上的二维均匀分布, 其中𝑫 = {(𝒙, 𝒚)|𝟎 < 𝒙 < 𝟔𝟎, 𝟎 < 𝒚 < 𝟔𝟎} 3
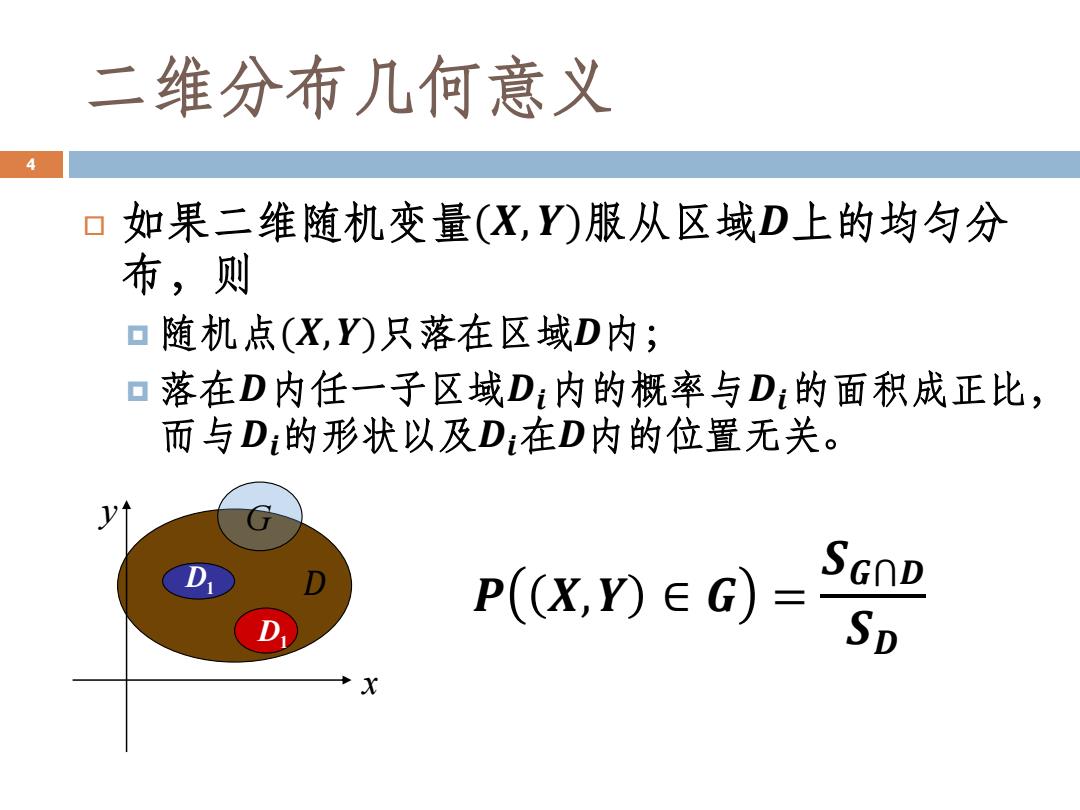
二维分布几何意义 4 如果二维随机变量(X,Y)服从区域D上的均匀分 布,则 口随机点(X,Y)只落在区域D内; ▣ 落在D内任一子区域D:内的概率与D:的面积成正比, 而与D:的形状以及D:在D内的位置无关。 SGAD P(x,)∈G)= Sp
二维分布几何意义 如果二维随机变量(𝑿,𝒀)服从区域𝑫上的均匀分 布,则 随机点(𝑿,𝒀)只落在区域𝑫内; 落在𝑫内任一子区域𝑫𝒊内的概率与𝑫𝒊的面积成正比, 而与𝑫𝒊的形状以及𝑫𝒊在𝑫内的位置无关。 4 𝐷 y x D1 D1 G 𝑷 𝑿,𝒀 ∈ 𝑮 = 𝑺𝑮⋂𝑫 𝑺𝑫

二维正态分布 5 口若二维随机变量(X,Y)具有密度函数 p(x,y) 1 -2n))门 其中u1,42,01>0,02>0,lp<1均为常数,则 称(X,)二维正态分布,记作 (X,Y)~N(1,2,oio2,p)
二维正态分布 若二维随机变量(𝑿, 𝒀)具有密度函数 𝒑 𝒙, 𝒚 = 𝟏 𝟐𝝅𝝈𝟏𝝈𝟐 𝟏 − 𝝆 𝟐 𝒆𝒙𝒑 ൝ ൡ − 𝟏 𝟐 𝟏 − 𝝆 𝟐 ൩ 𝒙 − 𝝁𝟏 𝝈𝟏 𝟐 − 𝟐𝝆 𝒙 − 𝝁𝟏 𝝈𝟏 𝒚 − 𝝁𝟐 𝝈𝟐 + 𝒚 − 𝝁𝟐 𝝈𝟐 𝟐 其中𝝁𝟏,𝝁𝟐,𝝈𝟏 > 𝟎,𝝈𝟐 > 𝟎, 𝝆 < 𝟏均为常数,则 称(𝑿,𝒀)二维正态分布,记作 𝑿,𝒀 ∼ 𝑵(𝝁𝟏,𝝁𝟐,𝝈𝟏 𝟐 ,𝝈𝟐 𝟐 ,𝝆) 5
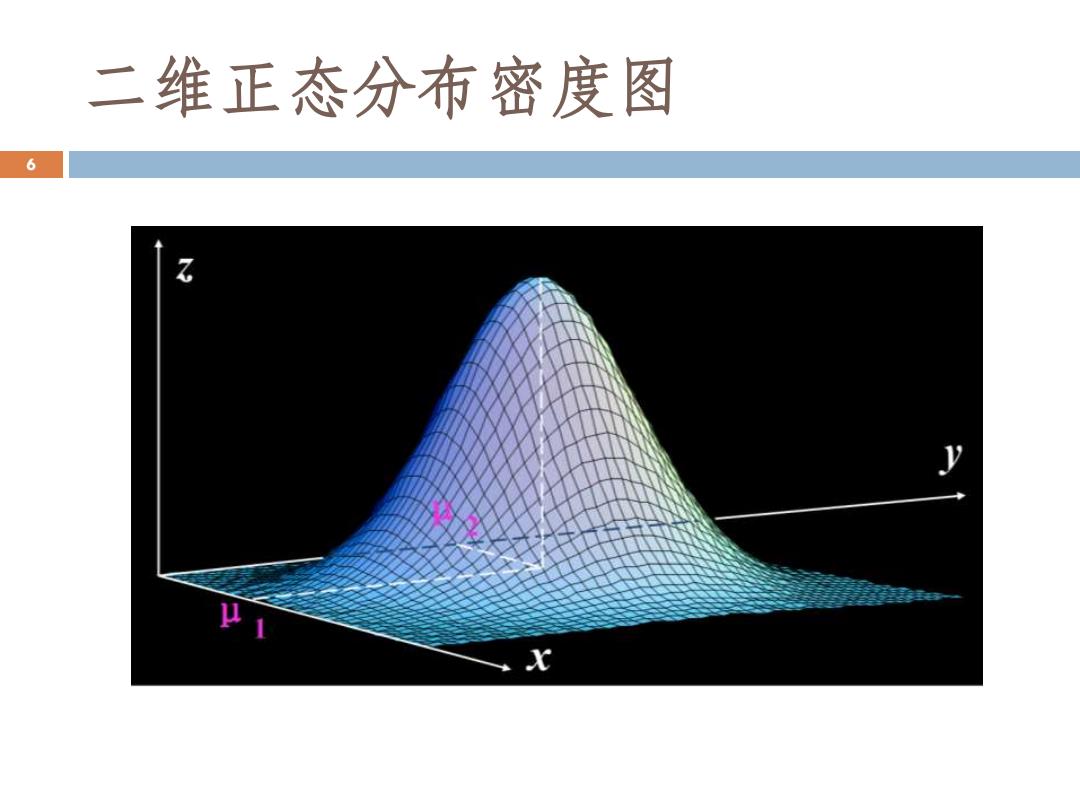
二维正态分布密度图 6 乙 y X
二维正态分布密度图 6

二维正态分布剖面图 7
二维正态分布剖面图 7

二维正态分布的边缘分布 8 口设(X,Y)~N(u1u2,oo2p),则 X~N(1,o),Y~N(2,o) 即:Px(x)= e 2元01 2a1,-00<X<十00 -2)2 pr(y)= 2mo2 2a吃,-00<y<+0 二维正态分布的边缘分布仍是正态分布 证:根据边缘分布的定义,换元积分即可
二维正态分布的边缘分布 设 𝑿, 𝒀 ∼ 𝑵 𝝁𝟏,𝝁𝟐,𝝈𝟏 𝟐 ,𝝈𝟐 𝟐 ,𝝆 ,则 𝑿 ∼ 𝑵 𝝁𝟏,𝝈𝟏 𝟐 ,𝒀 ∼ 𝑵 𝝁𝟐,𝝈𝟐 𝟐 即:𝒑𝑿 𝒙 = 𝟏 𝟐𝝅𝝈𝟏 𝒆 − 𝒙−𝝁𝟏 𝟐 𝟐𝝈𝟏 𝟐 , −∞ < 𝒙 < +∞ 𝒑𝒀 𝒚 = 𝟏 𝟐𝝅𝝈𝟐 𝒆 − 𝒚−𝝁𝟐 𝟐 𝟐𝝈𝟐 𝟐 , −∞ < 𝒚 < +∞ 8 二维正态分布的边缘分布仍是正态分布 证:根据边缘分布的定义,换元积分即可

二维正态随机变量的独立性 9 定理:设(X,Y)N(1,42,o1,吃,p),则 X,Y相互独立的充要条件为:p=0。 证明:p=0时,二维正态(X,)的密度函数: p(x,)= 2πo02V1-p ewp20'ply -2p(*4'二)+('-4)21]} ap,0gy]}
二维正态随机变量的独立性 9 定理:设 𝑿, 𝒀 ∼ 𝑵(𝝁𝟏,𝝁𝟐, 𝝈𝟏 𝟐 , 𝝈𝟐 𝟐 , 𝝆),则 𝑿, 𝒀相互独立的充要条件为:𝝆 = 𝟎

二维正态随机变量的独立性 10 e 1 (x- 1 (y-42 2o1 2o -e 2π01 √N2π02 Px(x)py(y) .随机变量X与Y相互独立
二维正态随机变量的独立性 10