
Advanced Algorithms Lovasz Local Lemma 尹一通Nanjing University,2022Fall
尹⼀通 Nanjing University, 2022 Fall Advanced Algorithms Lovász Local Lemma

k-SAT Conjunctive Normal Form(CNF): Liberals Φ=xVV)∧1VV4∧③V V7x5) clause Boolean variables:x1,x2,...,{True,False} k-CNF:each clause contains exactly k variables Problem(k-SAT) Input:k-CNF formula Output:determine whether is satisfiable. 。[Cook-Levin]NP-hard if k≥3
• Conjunctive Normal Form (CNF): Boolean variables: • -CNF: each clause contains exactly variables • [Cook-Levin] NP-hard if Φ = (x1 ∨ ¬x2 ∨ x3) ∧ (x1 ∨ x2 ∨ x4) ∧ (x3 ∨ ¬x4 ∨ ¬x5) x1, x2,…, xn ∈ {𝚃𝚛𝚞𝚎, 𝙵𝚊𝚕𝚜𝚎} k k k ≥ 3 k-SAT clause literals Problem ( -SAT) Input: -CNF formula . Output: determine whether is satisfiable. k k Φ Φ

Trivial Cases Problem (k-SAT) Input:k-CNF formula Output:determine whether is satisfiable. Clauses are disjoint: Φ=(x1V2Vx3)Λ(x4Vx5Vx6)Λ(xV7 Xs VX9). resolve each clause independently(is alwsays satisfiable!) 。m<2k=Φis always satisfiable. m:of clauses
Problem ( -SAT) Input: -CNF formula . Output: determine whether is satisfiable. k k Φ Φ • Clauses are disjoint: resolve each clause independently (Φ is always satisfiable!) • ⟹ is always satisfiable. Φ = (x1 ∨ ¬x2 ∨ x3) ∧ (x4 ∨ x5 ∨ x6) ∧ (x7 ∨ ¬x8 ∨ ¬x9) m < 2k Φ Trivial Cases m: # of clauses

The Probabilistic Method 。k-CNF:Φ=C1∧C2∧…∧Cm k variables Φ=(x1V7x2V3)∧(x1Vx2Vx4)Λ(5Vx4Vx5) Draw uniform random x1,x2,...,{True,False} Bad event A;:clause C;is violated V1≤i≤m,Pr[A=2-k ·Union bound:PrVA≤∑,PrAl=m2-t m0→is satisfiable: →r△-ia-m>o (independent bad events)
• -CNF: • Draw uniform random • Bad event : clause is violated • Union bound: disjoint clauses k Φ = C1 ∧ C2 ∧ ⋯ ∧ Cm Φ = (x1 ∨ ¬x2 ∨ x3) ∧ (x1 ∨ x2 ∨ x4) ∧ (x3 ∨ ¬x4 ∨ ¬x5) x1, x2, …, xn ∈ {𝚃𝚛𝚞𝚎, 𝙵𝚊𝚕𝚜𝚎} Ai Ci ∀1 ≤ i ≤ m, Pr[Ai ] = 2−k m 0 ⟹Pr [ m ⋀ i=1 Ai ] = m ∏ i=1 (1 − Pr[Ai ]) > 0 The Probabilistic Method k variables (independent bad events) ⟹ ⟹Φ is satisfiable! Pr [⋁m i=1Aj] ≤ ∑m i=1 Pr[Ai ] = m2−k

The Probabilistic Method Problem(k-SAT) Input:k-CNF formula Output:determine whether is satisfiable. ③WILEY ·uniform random x1,.,xm∈{True,False} disjoint clauses or →Pr[Φ(x)=True]>0 THE PROBABILISTIC m 0→3x∈2,(x) wiley-interscience Series in Discrete Mathematics and Optimization
• uniform random x1, …, xn ∈ {𝚃𝚛𝚞𝚎, 𝙵𝚊𝚕𝚜𝚎} The Probabilistic Method disjoint clauses or m 0 ∃x ∈ {𝚃, 𝙵}n ⟹ Φ(x) = 𝚃𝚛𝚞𝚎 The Probabilistic Method: Draw x from prob. space Ω: for property 𝒫, Pr[𝒫(x)] > 0 ⟹ ∃x ∈ Ω, 𝒫(x) Problem ( -SAT) Input: -CNF formula . Output: determine whether is satisfiable. k k Φ Φ

Limited Dependency 。k-CNF:Φ=C1AC2N…∧Cm k variables Φ=(x1Vx2Vx3)∧(x1Vx2Vx4)Λ(x3V74Vx5) Dependency degree d: each clause intersects d other clauses uniform random1,...,[T,F),each clause is violated w.p.2-k (union bound)m2k0 LLL)e(d+1)2k≤1丿 4d2-k≤1
• -CNF: • uniform random , each clause is violated w.p. k Φ = C1 ∧ C2 ∧ ⋯ ∧ Cm Φ = (x1 ∨ ¬x2 ∨ x3) ∧ (x1 ∨ x2 ∨ x4) ∧ (x3 ∨ ¬x4 ∨ ¬x5) x1, …, xn ∈ {𝚃, 𝙵} 2−k Limited Dependency k variables ⟹ Pr[ no clause is violated ] > 0 (union bound) m2−k < 1 } (“local” union bound?) d2−k < 1 (LLL) e(d + 1)2−k ≤ 1 Dependency degree : each clause intersects other clauses d ≤ d 4d2−k ≤ 1

Lovasz Local Lemma (LLL) ·“Bad”events A1,,A,where all Pr[Al≤p Dependency degree d: each A;is“dependent"of≤d other events Lovasz Local Lemma [Lovasz and Erd6s 1973;Lovasz 1977]: +s1一[可0 。The“LLL”condition: Bad events are not too likely to occur individually. Bad events are not too dependent with each other
Lovász Local Lemma [Lovász and Erdős 1973; Lovász 1977]: ep(d + 1) ≤ 1 • “Bad” events A , where all 1,…, Am Pr[Aj ] ≤ p Lovász Local Lemma (LLL) ⟹ Pr [ m ⋀ i=1 Ai ] > 0 Dependency degree : each is “dependent” of other events d Ai ≤ d • The “LLL” condition: • Bad events are not too likely to occur individually. • Bad events are not too dependent with each other

Dependency Graph ·“Bad”events A1,,Am Dependency degree d: each A;is mutually independent of all except d other events Definition (independence): A is independent of B if Pr[A B]Pr[A]or B is impossible. Ao is mutually independent of A1,...,A if Ao is independent of every event B=BA...A B,where each B;=A;or Aj
• “Bad” events A , 1,…, Am Dependency Graph Dependency degree : each is mutually independent of all except other events d Ai ≤ d Definition (independence): is independent of if or is impossible. is mutually independent of if is independent of every event , where each or . A B Pr[A ∣ B] = Pr[A] B A0 A1, …, Am A0 B = B1 ∧ ⋯ ∧ Bm Bi = Ai Ai
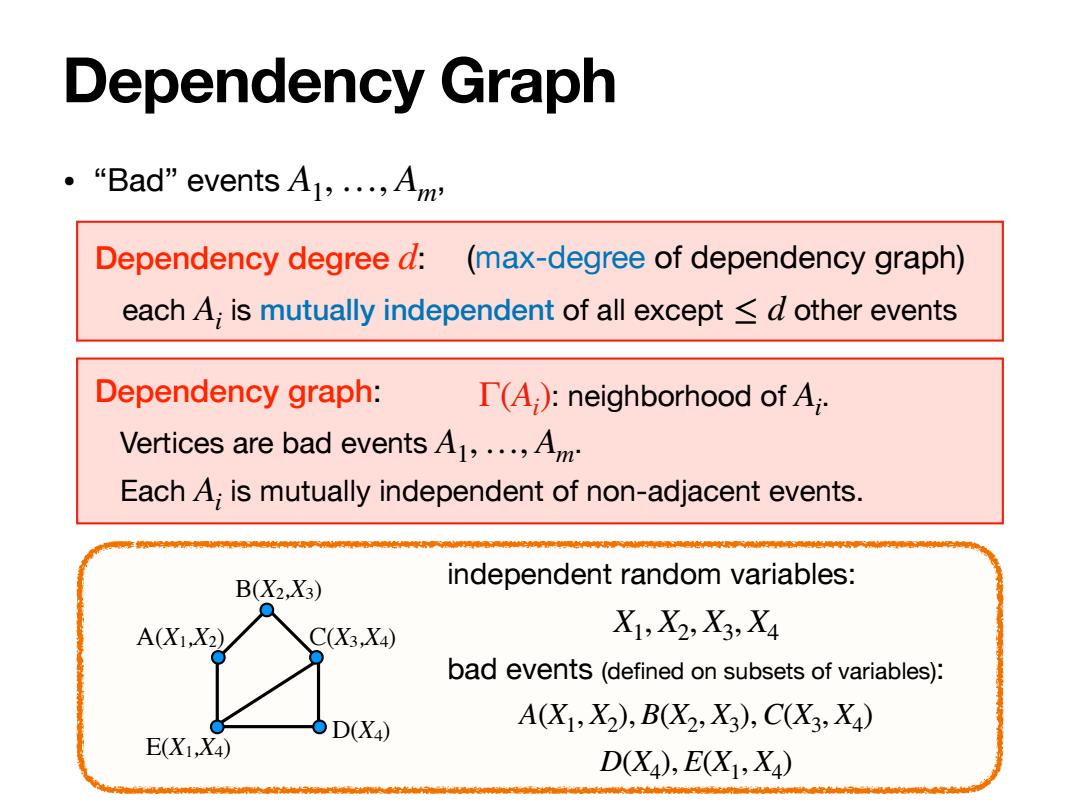
Dependency Graph ·“Bad"events A1,,Am: Dependency degree d: :(max-degree of dependency graph) each A;is mutually independent of all except d other events Dependency graph: T(A):neighborhood of A;. Vertices are bad events A,...,A Each A;is mutually independent of non-adjacent events. B(X2,X3) independent random variables: A(X1,X2) C(X3,X4) X1,X2,X3,X4 bad events (defined on subsets of variables): 6DX4) A(X1,X2),BX2,X3),C(X3,X4) E(X1,X4) D(X4),E(X1,X4)
Dependency Graph Dependency degree : each is mutually independent of all except other events d Ai ≤ d Dependency graph: Vertices are bad events . Each is mutually independent of non-adjacent events. A1, …, Am Ai (max-degree of dependency graph) A(X1,X2) B(X2,X3) C(X3,X4) E(X1,X4) D(X4) independent random variables: bad events (defined on subsets of variables): X1, X2, X3, X4 A(X1, X2), B(X2, X3),C(X3, X4) D(X4), E(X1, X4) Γ(A : neighborhood of . i ) Ai • “Bad” events A , 1,…, Am

Lovasz Local Lemma (LLL) A1,...A has a dependency graph given by neighborhoods I(): A;is mutually independent of all A;(A) Lovasz Local Lemma: p≌max;Pr[A,andd≌max;lT(A)l ep(d+1)≤1→Pr[∧1A>0
Lovász Local Lemma: p ≜ max and i Pr[Ai ] d ≜ maxi |Γ(Ai )| ep(d + 1) ≤ 1 ⟹ Pr[⋀m i=1Ai] > 0 Lovász Local Lemma (LLL) • has a dependency graph given by neighborhoods : is mutually independent of all A1, …, Am Γ( ⋅ ) Ai Aj ∉ Γ(Ai )