
本次课主要内容 图的宽直径简介 (一)、敏格尔定理 (二)、图的宽直径相关概念 (三)、一些主要研究结果简介
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (一)、敏格尔定理 (二)、图的宽直径相关概念 图的宽直径简介 (三)、一些主要研究结果简介

(一)、敏格尔定理 敏格尔定理是图的连通性问题的核心定理之一,它 描述了图的连通度与连通图中不同点对间的不相交路的 数目之间的关系。 定义1设u与v是图G的两个不同顶点,S表示G的 顶点子集或边子集,如果u与v不在G-S的同一分支上 称S分离u和v。 例如: {u1,u4},{u12u1u4,u4u}分离点u2与u6
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 敏格尔定理是图的连通性问题的核心定理之一,它 描述了图的连通度与连通图中不同点对间的不相交路的 数目之间的关系。 (一)、敏格尔定理 定义1 设u与v是图G的两个不同顶点,S表示G的一个 顶点子集或边子集,如果u与v不在G-S的同一分支上, 称S分离u和v。 例如: u6 u5 u2 u3 u4 u1 {u1, u4}, {u1u2, u1u4, u4u5}分离点u2与u6
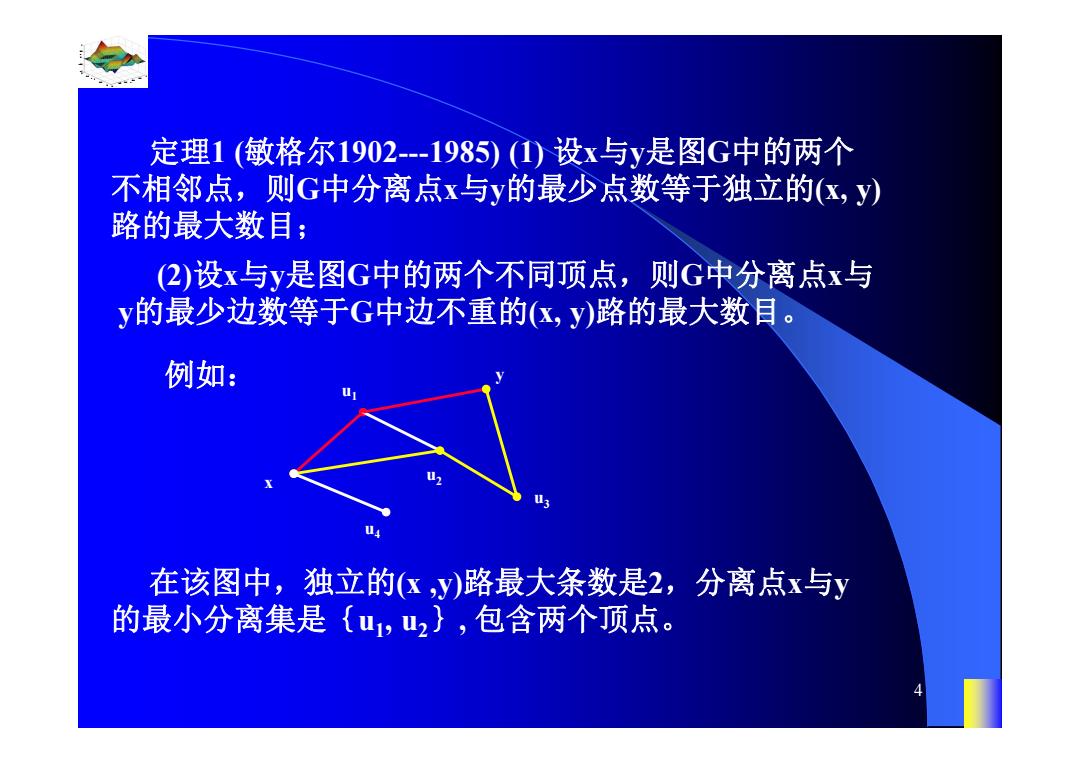
定理1(敏格尔1902-1985)(1)设x与y是图G中的两个 不相邻点,则G中分离点x与y的最少点数等于独立的(区,y) 路的最大数目; (2)设x与y是图G中的两个不同顶点,则G中分离点x与 y的最少边数等于G中边不重的(区,y)路的最大数目。 例如: 在该图中,独立的x,y)路最大条数是2,分离点x与y 的最小分离集是{u,u2},包含两个顶点
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 定理1 (敏格尔1902---1985) (1) 设x与y是图G中的两个 不相邻点,则G中分离点x与y的最少点数等于独立的(x, y) 路的最大数目; (2)设x与y是图G中的两个不同顶点,则G中分离点x与 y的最少边数等于G中边不重的(x, y)路的最大数目。 例如: x u4 y u3 u2 u1 在该图中,独立的(x ,y)路最大条数是2,分离点x与y 的最小分离集是{u1, u2}, 包含两个顶点

又在该图中,边不重的x,y)路最大条数是2,分离点x 与y的最小边分离集是{xu1,xu2},包含两条边。 该定理是图论中,也是通信理论中的最著名的定理之 一, 是由奥地利杰出数学家Mengeri在1927年发表的。 敏格尔(1902--1985)早年显示出数学物理天赋,1920 年入维也纳大学学习物理,次年,由于参加德国物理学家 Hans Hahn的“曲线概念的新意”讲座,而把兴趣转向了 数学。因为Has提到当时没有满意的曲线概念定义,包括 大数学家康托、约当,豪斯道夫等都尝试过,没有成功
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 x u4 y u3 u2 u1 又在该图中,边不重的(x ,y)路最大条数是2,分离点x 与y的最小边分离集是{xu1, xu2}, 包含两条边。 该定理是图论中,也是通信理论中的最著名的定理之 一,是由奥地利杰出数学家Menger在1927年发表的。 敏格尔(1902---1985)早年显示出数学物理天赋,1920 年入维也纳大学学习物理,次年,由于参加德国物理学家 Hans Hahn的“曲线概念的新意”讲座,而把兴趣转向了 数学。因为Hans提到当时没有满意的曲线概念定义,包括 大数学家康托、约当,豪斯道夫等都尝试过,没有成功

而且,认为不可能彻底解决。但是,尽管作为几乎没有数 学背景的本科生,通过自己的努力,敏格尔还是解决了该 问题。由此,他就转向曲线和维数理论的研究。 敏格尔本科期间,身体很差,父母双亡。但在1924年 在Hahn指导下完成了他的研究工作。1927年做了维也纳 大学几何学首席教授,同年,发表了“一弧定理”,即 敏格尔定理。 1930年,敏格尔来到匈牙利布达佩斯做访问,当时哥 尼正在写一本书,要囊括图论中的所有知名定理。敏格尔 向他推荐自己的定理,但哥尼最初不相信他,认为敏格尔 定理一定不对,花了一个晚上找反例试图否定敏格尔定理, 但没有成功,于是要了敏格尔的证明,终于把敏格尔定理 加在了他的著作的最后一节。 敏格尔被认为是20世纪最杰出数学家之一
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 而且,认为不可能彻底解决。但是,尽管作为几乎没有数 学背景的本科生,通过自己的努力,敏格尔还是解决了该 问题。由此,他就转向曲线和维数理论的研究。 敏格尔本科期间,身体很差,父母双亡。但在1924年 在Hahn指导下完成了他的研究工作。1927年做了维也纳 大学几何学首席教授,同年,发表了“n—弧定理”,即 敏格尔定理。 1930年,敏格尔来到匈牙利布达佩斯做访问,当时哥 尼正在写一本书,要囊括图论中的所有知名定理。敏格尔 向他推荐自己的定理,但哥尼最初不相信他,认为敏格尔 定理一定不对,花了一个晚上找反例试图否定敏格尔定理, 但没有成功,于是要了敏格尔的证明,终于把敏格尔定理 加在了他的著作的最后一节。 敏格尔被认为是20世纪最杰出数学家之一

哈恩(1879~1968)德国物理学家,化学家。最大的贡 献是1938年和F.斯特拉斯曼一起发现核裂变现象。哈恩获 得1944年诺贝尔化学奖。 借助于敏格尔定理,数学家惠特尼在1932年的博士论 文中给出了k连通图的一个美妙刻画。这就是人们熟知的 所谓“敏格尔定理” 定理2(惠特尼1932)一个非平凡的图G是kk≥2)连通的, 当且仅当G的任意两个顶点u与v间,至少存在k条内点不交 的(u,v)路。 证明:(必要性)设G是kk≥2)连通的,u与v是G的两个 顶点。 情形1:如果u与v不相邻,U为G的最小u-v分离集,那么有 U≥k(G)≥k,于是由敏格尔定理,结论成立;
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 哈恩 (1879~1968 ) 德国物理学家,化学家。最大的贡 献是1938年和F.斯特拉斯曼一起发现核裂变现象。哈恩获 得1944年诺贝尔化学奖 。 借助于敏格尔定理,数学家惠特尼在1932年的博士论 文中给出了k连通图的一个美妙刻画。这就是人们熟知的 所谓“敏格尔定理” 定理2 (惠特尼1932) 一个非平凡的图G是k (k≧2)连通的, 当且仅当G的任意两个顶点u与v间,至少存在k条内点不交 的(u ,v)路。 证明: (必要性) 设G是k (k≧2)连通的,u与v是G的两个 顶点 。 情形1:如果u与v不相邻,U为G的最小u--v分离集,那么有 |U| ≧ k (G) ≧ k,于是由敏格尔定理,结论成立;

情形2:若u与v邻接,其中e=uv,那么,容易证明:G-e 是(k-1)连通的。由情形1知:G-e至少包含k-1条内点不交 的u-v路,即G至少包含k条内点不交的u-v路。 (充分性)假设G中任意两个顶点间至少存在k条内部 不交路。设U是G的最小顶点割,即U=k(G)。令x与y是 G-U的处于不同分支的两个点。所以U是x与y的分离集, 由敏格尔定理:U≥k,即证明G是k连通的。 例1设G是k连通图,S是由G中任意k个顶点构成的集 合。若图H是由G通过添加一个新点w以及连接w到S中所 有顶点得到的新图,求证:H是k连通的。 证明:首先,分离G中两个不相邻顶点至少要k个点, 其次,分离w与G中不在S中顶点需要k个顶点。因此H是k 连通的
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 情形2:若u与v邻接,其中e=uv,那么,容易证明:G-e 是(k-1)连通的。由情形1知:G-e至少包含k-1条内点不交 的u--v路,即G至少包含k条内点不交的u--v路。 (充分性) 假设G中任意两个顶点间至少存在 k 条内部 不交路。设U是G的最小顶点割,即|U|=k (G)。令x与y是 G-U的处于不同分支的两个点。所以U是x与y的分离集, 由敏格尔定理:|U| ≧ k, 即证明G是 k 连通的。 例1 设G是k连通图,S是由G中任意k个顶点构成的集 合。若图H是由G通过添加一个新点w以及连接w到S中所 有顶点得到的新图,求证:H是k连通的。 证明:首先,分离G中两个不相邻顶点至少要k个点, 其次,分离w与G中不在S中顶点需要k个顶点。因此H是k 连通的

例2设G是k连通图,u,VY2,V为G中k+1个不同顶 点。求证:G中有k条内点不交路(u,)(1≤i至k) 证明:在G外添加一点w,让w与v邻接(1ik)得H, H
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 例2 设G是k连通图,u , v1,v2,…,vk为G中k+1个不同顶 点。求证:G中有k条内点不交路(u ,vi) (1≦i≦k) 证明:在G外添加一点w,让w与vi邻接(1≦i≦k)得H. G v1 u v2 vk H v1 u v2 vk w

由例1,H是k连通的,于是由定理2,u与w间存在k条 内点不交的u--w路,所以G中有k条内点不交路(u,) (1sisk)。 对于边连通度,有类似定理: 定理3(惠特尼1932)一个非平凡的图G是kk≥2)边连 通的,当且仅当G的任意两个顶点间至少存在k条边不重的 (u,v)路。 推论对于一个阶至少为3的无环图G,下面三个命题等价。 (1)G是2连通的: (2)G中任意两点位于同一个圈上; (3)G无孤立点,且任意两条边在同一个圈上。 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 由例1,H是k连通的,于是由定理2,u与w间存在k条 内点不交的u---w路,所以 G中有k条内点不交路(u ,vi) (1≦i≦k)。 对于边连通度,有类似定理: 定理3 (惠特尼1932) 一个非平凡的图G是k (k≧2)边连 通的,当且仅当G的任意两个顶点间至少存在k条边不重的 (u ,v)路。 推论 对于一个阶至少为3的无环图G,下面三个命题等价。 (1) G是2连通的; (2) G中任意两点位于同一个圈上; (3) G无孤立点,且任意两条边在同一个圈上

证明:(1)→(2) G是2连通的,则G的任意两个顶点间存在两条内点不交 路P与P,显然这两条路构成包含该两个项点的圈。 (2)→(3) G无孤立点显然。设e,与e是G的任意两条边,在e,与e2上 分别添加两点u与v得图H,则H是2连通的,由(1)→(2),H的 任意两个顶点在同一个圈上,即u与v在同一个圈上,也即e 与e2在同一个圈上。 (3)→(1) 设u与v是无环图G的任意两个不相邻顶点,由于G无孤立 点,所以可设e1,e2分别与u,v相关联。由(3),e1,e2在同 一个圈上,所以u与v在同一个圈上,因此分离u与v至少要 去掉两个顶点,即证明G是2连通的
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 证明:(1)→(2) G是2连通的,则G的任意两个顶点间存在两条内点不交 路P1与P2,显然这两条路构成包含该两个顶点的圈。 G无孤立点显然。设e1与e2是G的任意两条边,在e1与e2上 分别添加两点u与v得图H,则H是2连通的,由(1)→(2),H的 任意两个顶点在同一个圈上,即u与v在同一个圈上,也即e1 与e2在同一个圈上。 (2)→(3) (3)→(1) 设u与v是无环图G的任意两个不相邻顶点,由于G无孤立 点,所以可设e1,e2分别与u, v相关联。由(3),e1,e2在同 一个圈上,所以u与v在同一个圈上,因此分离u与v至少要 去掉两个顶点,即证明G是2连通的