
本次课主要内容 与色数有关的几类图和完美图 (一)、与色数有关的几类图 (二)、完美图简介
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (一)、与色数有关的几类图 (二)、完美图简介 与色数有关的几类图和完美图

(一)、与色数有关的几类图 1、临界图 定义1若对图G的任意真子图H,都有H)<G,则 称G是临界图。点色数为k的临界图称为k临界图。 3临界图 非临界图 4临界图 注:临界图由狄拉克在1952年首先提出并研究。上面 的4临界图是Grotzsch(格勒奇)在1958年提出的
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 1、临界图 (一)、与色数有关的几类图 定义1 若对图G的任意真子图H,都有 ,则 称G是临界图。点色数为k的临界图称为k临界图。 ( ) () H G 3临界图 4临界图 非临界图 注:临界图由狄拉克在1952年首先提出并研究。上面 的4临界图是Grotzsch(格勒奇)在1958年提出的

定理1临界图有如下性质 (1)k色图均有k临界子图; (2)每个临界图均为简单连通图; (3)若G是k临界图,则6≥k-1。 证明:(1)是显然的。 (2)因为删掉环或平行边中的一条边并不破坏原有的顶 点正常着色,所以每个临界图是单图;又因为删掉色数 较小的分支,剩下部分的图的色数和原图色数相等,所 以,临界图必须是连通图
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 定理1 临界图有如下性质 (1) k色图均有k临界子图; (2) 每个临界图均为简单连通图; (3) 若G是k临界图,则δ≥k-1。 证明: (1)是显然的。 (2) 因为删掉环或平行边中的一条边并不破坏原有的顶 点正常着色,所以每个临界图是单图;又因为删掉色数 较小的分支,剩下部分的图的色数和原图色数相等,所 以,临界图必须是连通图

(3)若不然,8<k-1。 设d(w)=δ。因为G是k临界图,所以G-v是k-1可正常顶 点着色的。设n是G-v的k-1正常顶点着色方案,显然, 它可以扩充为G的k-1正常点着色方案。这与G是k临界图 相矛盾。 推论:每个k色图至少有k个度不小于k-1的顶点。 证明:因G是k色图,所以,它包含k临界子图G所以 有:8(G)≥k-1,即G中至少有k个顶点,其度数不小于 k-1。所以,G中至少有k个度不小于k-1的顶点。 例1利用上面推论证明:对任意图G,有: X(G)≤△(G)+1
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 (3) 若不然,δ< k-1。 设d(v)=δ。因为G是k临界图,所以G-v是k-1可正常顶 点着色的。设п是G-v的k-1正常顶点着色方案,显然, 它可以扩充为G的k-1正常点着色方案。这与G是k临界图 相矛盾。 推论:每个k色图至少有k个度不小于k-1的顶点。 证明:因G是k色图,所以,它包含k临界子图G1,所以 有:δ(G1)≥k-1,即G1中至少有k个顶点,其度数不小于 k-1。所以,G中至少有k个度不小于k-1的顶点。 例1 利用上面推论证明:对任意图G,有: () ()1 G G

证明:设G的点色数为 。由推论,G中至少有 x(G》 个顶点,其度数不小于 x(G)-1 所以,A(G)≥X(G)-I,即:(G)≤△(G)+1 例2求证:临界图没有割点。 证明:设G是k临界图。如果G有割点y设G1,G2,,G,是 G-v的分支。又设第i个分支顶点集为V,(I≤i≤r)。 设H=GV,U{v}],(1ir)。则H是k-1可正常点着色 的,现对每个H进行k-1正常点着色,且v都分配同一种颜色, 那么,将着色后的H合在一起,得到G的k-1正常点着色方 案,这与G是k色图矛盾。所以临界图没有割点
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 证明:设G的点色数为 。由推论,G中至少有 个顶点,其度数不小于 () ()1 G G ( ) G ( ) G ()1 G 所以, ,即: () ()1 G G 例2 求证:临界图没有割点。 证明:设G是k临界图。如果G有割点v, 设G1,G2,…,Gr是 G-v的分支。又设第i个分支顶点集为Vi (1≦i≦r)。 设Hi=G[Vi∪{v}], (1≦i≦r)。则Hi是k-1可正常点着色 的,现对每个Hi进行k-1正常点着色,且v都分配同一种颜色, 那么,将着色后的Hi合在一起,得到G的k-1正常点着色方 案,这与G是k色图矛盾。所以临界图没有割点

例3求证:仅有的1临界图是k;仅有的2临界图是K2;仅 有的3临界图奇圈。 证明:由于1色图是空图,所以1临界图只能是K:2色 图是偶图,所以,2临界图只能是K2;3色图必然含有奇圈, 而奇圈的色数是3,所以,3临界图只能是奇圈。 例4求证:布鲁克斯定理等价于下述命题:若G是k临 界图k②4),且不是完全图,则2m≥nk-1)+1,其中m为G的 边数而n为顶点数。 证明:(1)由布鲁克斯定理推例4中命题。 因G是k临界图,所以G是连通单图,又k≥4,所以G不能 是奇圈,再由G不是完全图,所以由布鲁克斯定理有
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 例3 求证:仅有的1临界图是k1;仅有的2临界图是K2;仅 有的3临界图奇圈。 证明:由于1色图是空图,所以1临界图只能是K1;2色 图是偶图,所以,2临界图只能是K2; 3色图必然含有奇圈, 而奇圈的色数是3,所以,3临界图只能是奇圈。 例4 求证:布鲁克斯定理等价于下述命题:若G是k临 界图(k≥4), 且不是完全图,则2m≥n(k-1)+1,其中m为G的 边数而n为顶点数。 证明:(1) 由布鲁克斯定理推例4中命题。 因G是k临界图,所以G是连通单图,又k≥4, 所以G不能 是奇圈,再由G不是完全图,所以由布鲁克斯定理有

k至△。 再由k临界图的性质,有δ≥k1.所以: 2m= ∑d(v)≥△+(n-1)δ vEV(G) ≥k+(n-1)(k-1) =n(k-1)+1 (2)由例4中命题推布鲁克斯定理。 因为连通单图G不是奇圈,也不是完全图。设G的k临 界子图是H。 情形1,H是奇圈。 在这种情况下,由于G不是奇圈,所以,H之外必然 有边和H相连,即△(G)≥3,另一方面,k(G)=k(H)=3,所
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 k≦Δ。 再由k临界图的性质,有δ≥k-1.所以: ( ) 2 ( ) ( 1) vVG m dv n kn k ( 1)( 1) n k( 1) 1 (2) 由例4中命题推布鲁克斯定理。 因为连通单图G不是奇圈,也不是完全图。设G的k临 界子图是H。 情形1, H是奇圈。 在这种情况下,由于G不是奇圈,所以,H之外必然 有边和H相连,即Δ(G)≥3,另一方面,k(G)=k(H)=3,所

以,k(G)至△(G); 情形2,H是完全图HK 在这种情况下,由于G是连通的非完全图,那么在H 之外,必然有边和H相连,即△≥K()=k(G): 情形3,H既不是奇圈又不是完全图,由例3知道, k≥4。H满足例4中条件。 所以,由例4中的结论有: △(H)n(H)≥2m(H)≥n(H)(k(H)-1)+1 =n(H)(k(G)-1)+1 所以,有: △(H)≥(k(G)-1)+ n(H
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 以,k(G)≦Δ(G); 情形2, H是完全图HK 在这种情况下,由于G是连通的非完全图,那么在H 之外,必然有边和H相连,即Δ≥K(H)=k(G); 情形3, H既不是奇圈又不是完全图,由例3知道, k≥4。H满足例4中条件。 所以,由例4中的结论有: ( ) ( ) 2 ( ) ( )( ( ) 1) 1 HnH mH nH kH nH kG ( )( ( ) 1) 1 所以,有: 1 ( ) ( ( ) 1) ( ) H kG n H

即证明: △(G)≥k(G) 2、唯一可着色图 对图的顶点进行正常着色,实际上给出图的顶点集合的一 种划分,不同的着色方案,给出的划分一般不同。但是,也 存在一类特殊图,对于任意的最优着色方案,导出的顶点划 分却是相同的。为此,我们给出如下定义。 定义2设简单标定图G的点色数是k,如果在任意的k正 常点着色方案下,导出的顶点集合划分唯一,称G是唯 一k可着色图,简称唯一可着色图。 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 即证明: () () G kG 2、唯一可着色图 对图的顶点进行正常着色,实际上给出图的顶点集合的一 种划分,不同的着色方案,给出的划分一般不同。但是,也 存在一类特殊图,对于任意的最优着色方案,导出的顶点划 分却是相同的。为此,我们给出如下定义。 定义2 设简单标定图G的点色数是k, 如果在任意的k正 常点着色方案下,导出的顶点集合划分唯一,称G是唯 一k可着色图,简称唯一可着色图
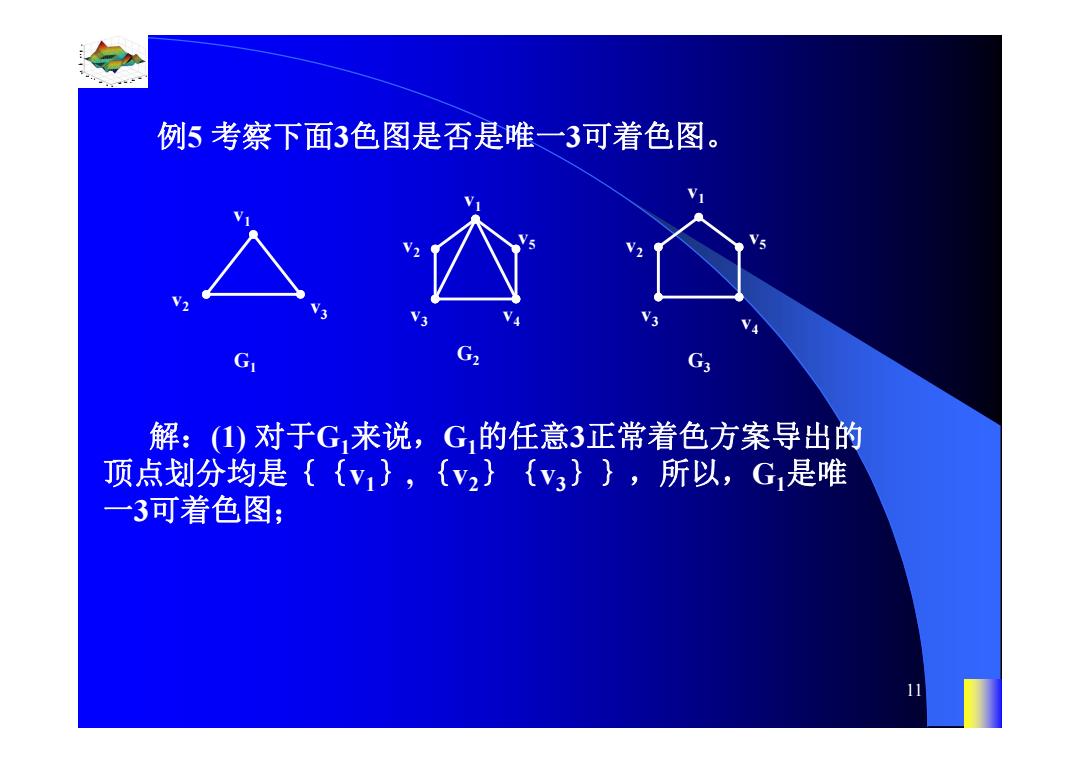
例5考察下面3色图是否是唯一3可着色图。 G 解:(1)对于G来说,G,的任意3正常着色方案导出的 顶点划分均是{(v},{v2}{y3}},所以,G1是唯 一3可着色图;
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 例5 考察下面3色图是否是唯一3可着色图。 v3 v2 v1 G1 v1 G2 v5 v3 v4 v2 G3 v5 v4 v3 v2 v1 解:(1) 对于G1来说,G1的任意3正常着色方案导出的 顶点划分均是{{v1}, {v2}{v3}},所以,G1是唯 一3可着色图;