
本次课主要内容 欧拉图与中国邮路问题 (一)、欧拉图及其性质 (二)、Fleury算法 (三)、中国邮路问题
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 本次课主要内容 (一)、欧拉图及其性质 (二)、Fleury算法 (三)、中国邮路问题 欧拉图与中国邮路问题
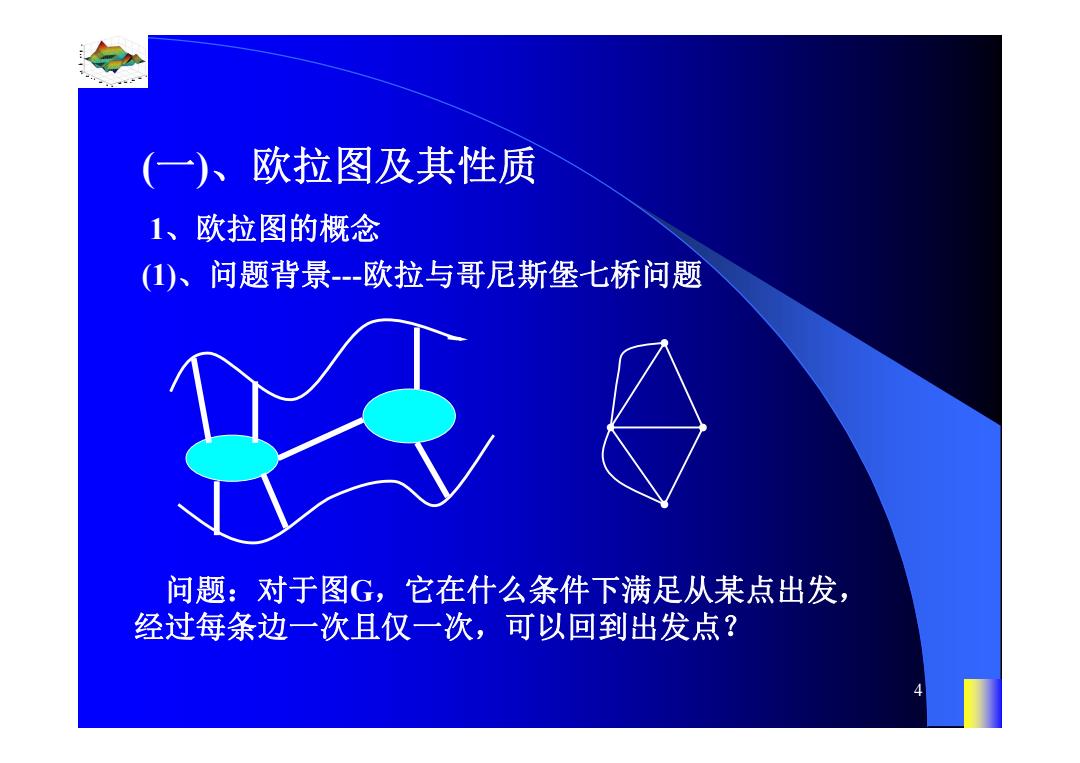
(一)、欧拉图及其性质 1、欧拉图的概念 (1)、问题背景-欧拉与哥尼斯堡七桥问题 问题:对于图G,它在什么条件下满足从某点出发, 经过每条边一次且仅一次,可以回到出发点?
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 1、欧拉图的概念 (一)、欧拉图及其性质 (1)、问题背景---欧拉与哥尼斯堡七桥问题 问题:对于图G,它在什么条件下满足从某点出发, 经过每条边一次且仅一次,可以回到出发点?

哥尼斯堡城(位于德国北部),在欧拉的生活与图论历 史中扮演着非常重要角色。因为它,产生了著名的欧拉 图定理,因为它,产生了图论。 注:一笔画--一中国古老的民间游戏 要求:对于一个图G,笔不离纸,一笔画成。 (2)、欧拉图概念 定义1对于连通图G,如果G中存在经过每条边的闭 迹,则称G为欧拉图,简称G为E图。欧拉闭迹又称为 欧拉环游,或欧拉回路。 3 欧拉图 非欧拉图 非欧拉图 有欧拉迹 无欧拉迹
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 哥尼斯堡城(位于德国北部), 在欧拉的生活与图论历 史中扮演着非常重要角色。因为它,产生了著名的欧拉 图定理,因为它,产生了图论。 注:一笔画----中国古老的民间游戏 要求:对于一个图G, 笔不离纸, 一笔画成. (2)、欧拉图概念 定义1 对于连通图G,如果G中存在经过每条边的闭 迹,则称G为欧拉图,简称G为E图。欧拉闭迹又称为 欧拉环游,或欧拉回路。 欧拉图 4 1 3 2 4 1 3 2 非欧拉图 有欧拉迹 非欧拉图 无欧拉迹 1 2 3 4

2、欧拉图的性质 定理1下列陈述对于非平凡连通图G是等价的: 1)G是欧拉图; (2)G的顶点度数为偶数; (3)G的边集合能划分为圈。 证明:(1)→(2) 由(1),设C是欧拉图G的任一欧拉环游,v是G中任 意顶点,v在环游中每出现一次,意味在G中有两条不 同边与v关联,所以,在G中与v关联的边数为偶数,即 v的度数为偶数,由v的任意性,即证明(2)。 (2)→(3) 由于G是连通非平凡的且每个顶点度数为偶数,所以 G中至少存在圈C,从G中去掉C,中的边,得到G的生成
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 2、欧拉图的性质 定理1 下列陈述对于非平凡连通图G是等价的: (1) G是欧拉图; (2) G的顶点度数为偶数; (3) G的边集合能划分为圈。 证明: (1)→(2) 由(1),设 C是欧拉图G的任一欧拉环游,v是G中任 意顶点,v在环游中每出现一次,意味在G中有两条不 同边与v关联,所以,在G中与v关联的边数为偶数,即 v的度数为偶数,由v的任意性,即证明(2)。 (2)→(3) 由于G是连通非平凡的且每个顶点度数为偶数,所以 G中至少存在圈C1,从G中去掉C1中的边,得到G的生成

子图G,若G,没有边,则3)成立。否则,G的每个非平 凡分支是度数为偶数的连通图,于是又可以抽取一个圈。 反复这样抽取,E(G)最终划分为若干圈。 (3)→(1) 设C,是G的边划分中的一个圈。若G仅由此圈组成, 则G显然是欧拉图。 否则,由于G连通,所以,必然存在圈C2,它和C有 公共顶点。于是,CUC2是一条含有C与C2的边的欧拉 闭迹,如此拼接下去, 得到包含G的所有边的一条欧拉 闭迹。即证G是欧拉图。 推论1连通图G是欧拉图当且仅当G的顶点度数为偶。 推论2连通非欧拉图G存在欧拉迹当且仅当G中只有两 个顶点度数为奇数
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 子图G1,若G1没有边,则(3)成立。否则,G1的每个非平 凡分支是度数为偶数的连通图,于是又可以抽取一个圈。 反复这样抽取,E(G)最终划分为若干圈。 (3)→(1) 设C1是G的边划分中的一个圈。若G仅由此圈组成, 则G显然是欧拉图。 否则,由于G连通,所以,必然存在圈C2,它和C1有 公共顶点。于是,C1∪C2是一条含有C1与C2的边的欧拉 闭迹,如此拼接下去,得到包含G的所有边的一条欧拉 闭迹。即证G是欧拉图。 推论1 连通图G是欧拉图当且仅当G的顶点度数为偶。 推论2 连通非欧拉图G存在欧拉迹当且仅当G中只有两 个顶点度数为奇数

例1下面图中谁是欧拉图?谁是非欧拉图但存在欧拉 迹?谁是非欧拉图且不存在欧拉迹? G G: 解:G是欧拉图;G,是非欧拉图,但存在欧拉迹;G 中不存在欧拉迹。 例2证明:若G和H是欧拉图,则G×H是欧拉图
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 例1 下面图中谁是欧拉图?谁是非欧拉图但存在欧拉 迹?谁是非欧拉图且不存在欧拉迹? G1 G2 G3 解:G1是欧拉图;G2是非欧拉图,但存在欧拉迹;G3 中不存在欧拉迹。 例2 证明:若G和H是欧拉图,则 是欧拉图。 G H

证明:首先证明:对任意m∈V(G),v∈V田,有: d(u)+d()=d(u,v)》 事实上,设z是u的任意一个邻点,一定有(u,v)的一个 邻点(z,v),反之亦然。同理,对于v的任意一个邻点w, 一定有(u,v)的一个邻点(u,w),反之亦然。即:(u,)在乘 积图中邻点个数等于u在G中邻点个数与v在H中邻点个 数之和。 所以,G,H是欧拉图,那么G×H顶点度数为偶数 其次证明: GxH 是连通的 (4,y),(42,y2)∈V(G×H) 由于G,H都是欧拉图,所以都连通。 设最短的u1-u2路
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 证明:首先证明:对任意u ∈V(G), v ∈V(H),有: du dv d uv ( ) ( ) (( , )) 事实上,设z是u的任意一个邻点,一定有(u, v)的一个 邻点(z, v),反之亦然。同理,对于v的任意一个邻点w, 一定有(u, v)的一个邻点(u, w), 反之亦然。即: (u, v)在乘 积图中邻点个数等于u在G中邻点个数与v在H中邻点个 数之和。 所以,G ,H是欧拉图,那么 顶点度数为偶数。 G H 其次证明: 是连通的。 G H 11 2 2 ( , ),( , ) ( ) u v u v VG H 由于G, H都是欧拉图,所以都连通。设最短的u1--u2路

最短的v1-V路分别为: u xx,6 xkuz Viy y26 ymV2 那么,由乘积图的定义: 在乘积图中有路: (41,y(x,y)6(xk,)(u2,y)(42,y)6(2,ym(42,Y2) 这样,我们证明了G×H是连通的且每个顶点度数为偶 数。即它是欧拉图。 (二)、Fleury(弗勒里)算法 该算法解决了在欧拉图中求出一条具体欧拉环游的方 法。方法是尽可能避割边行走。 算法 (1)小 任意选择一个顶点V,置w=V; 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 最短的v1--v2路分别为: uxx xu 112 2 L k 112 2 m vyy y v L 那么,由乘积图的定义:在乘积图中有路: 11 11 1 21 2 1 2 2 2 ( , )( , ) ( , )( , )( , ) ( , )( , ) uv xv x v u v u y u y u v L L k m 这样,我们证明了 是连通的且每个顶点度数为偶 数。即它是欧拉图。 G H (二)、Fleury(弗勒里)算法 该算法解决了在欧拉图中求出一条具体欧拉环游的方 法。方法是尽可能避割边行走。 算法: (1)、 任意选择一个顶点v0,置w0=v0;

(2)、假设迹w,-voeY1eY,已经选定,那么按下述方 法从E-{e1e2,e,)中选取边e+ 1)、e#1与v相关联: 2)、除非没有别的边可选择,否则e+1不能是 G=G{e1e2,e:}的割边。 3)、当(2)不能执行时,算法停止。 例3在下面欧拉图G中求一条欧拉回路。 b 图G
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 (2)、 假设迹wi=v0e1v1…eivi已经选定,那么按下述方 法从E-{e1,e2,…,ei}中选取边ei+1: 1)、 ei+1与vi相关联; 2)、除非没有别的边可选择,否则 ei+1不能是 Gi=G-{e1,e2,…,ei}的割边。 (3)、 当(2)不能执行时,算法停止。 例3 在下面欧拉图G中求一条欧拉回路。 d c b a f e g 图G h j i
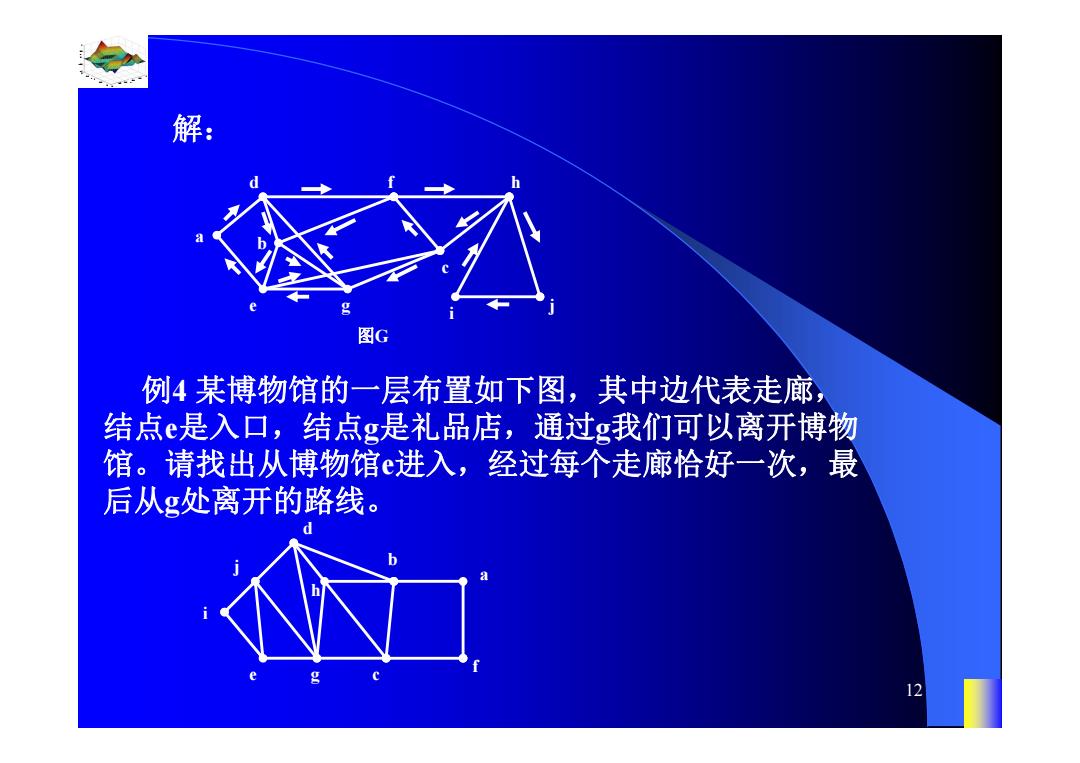
解: 图G 例4某博物馆的一层布置如下图,其中边代表走廊, 结点是入口,结点g是礼品店,通过g我们可以离开博物 馆。请找出从博物馆进入,经过每个走廊恰好一次,最 后从g处离开的路线。 12
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 12 解: d c b a f e g 图G h j i 例4 某博物馆的一层布置如下图,其中边代表走廊, 结点e是入口,结点g是礼品店,通过g我们可以离开博物 馆。请找出从博物馆e进入,经过每个走廊恰好一次,最 后从g处离开的路线。 a f e d c b i h g j