
电↓科越女学 r街y时Bectrele8 cad Tecaology af Chiaa /956 本次课内容 一、图论简介 二、图的定义及其相关概念 三、图的同构
本次课内容 一、图论简介 二、图的定义及其相关概念 三、图的同构
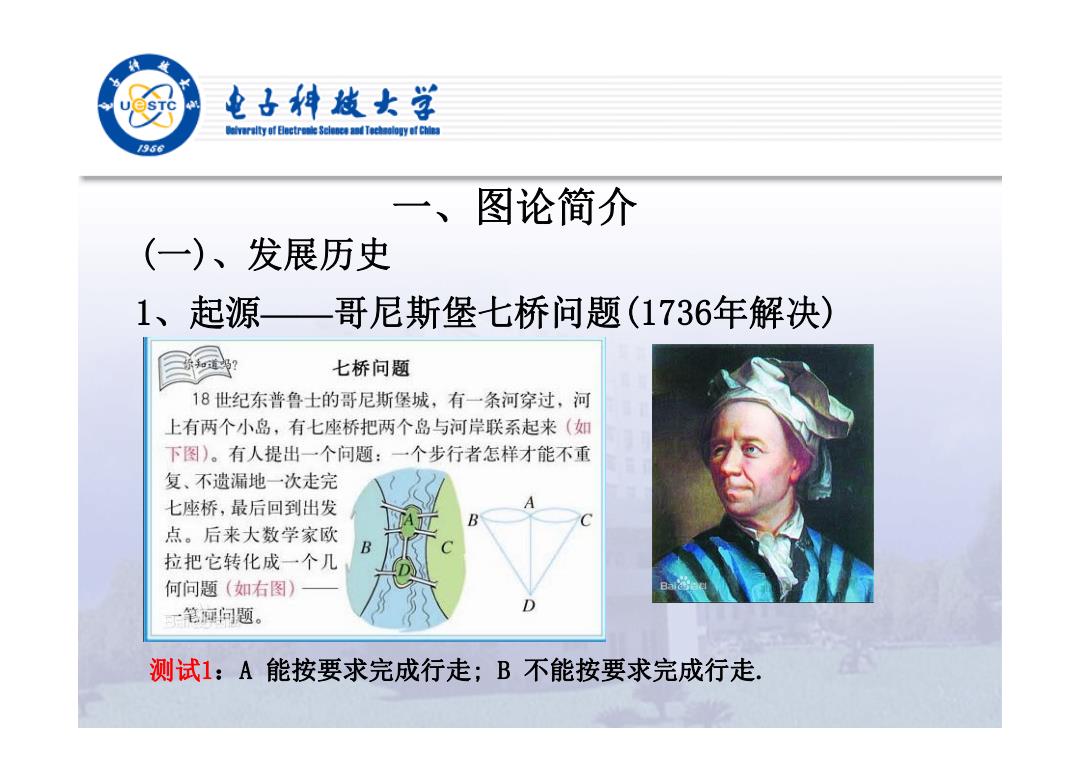
电↓科放女学 r街y时Bectrele8 ciad Tecaology af Chins /956 一、 图论简介 (一)、发展历史 1、起源一哥尼斯堡七桥问题(1736年解决) 食@ 七桥问题 18世纪东普鲁土的哥尼斯堡城,有一条河穿过,河 上有两个小岛,有七座桥把两个岛与河岸联系起来(如 下图)。有人提出一个问题:一个步行者怎样才能不重 复、不遗漏地一次走完 七座桥,最后回到出发 点。后来大数学家欧 B 拉把它转化成一个几 何问题(如右图) 一笔闻问题。 测试1:A能按要求完成行走;B不能按要求完成行走
一、图论简介 (一)、发展历史 1、起源——哥尼斯堡七桥问题(1736年解决) 测试1:A 能按要求完成行走; B 不能按要求完成行走
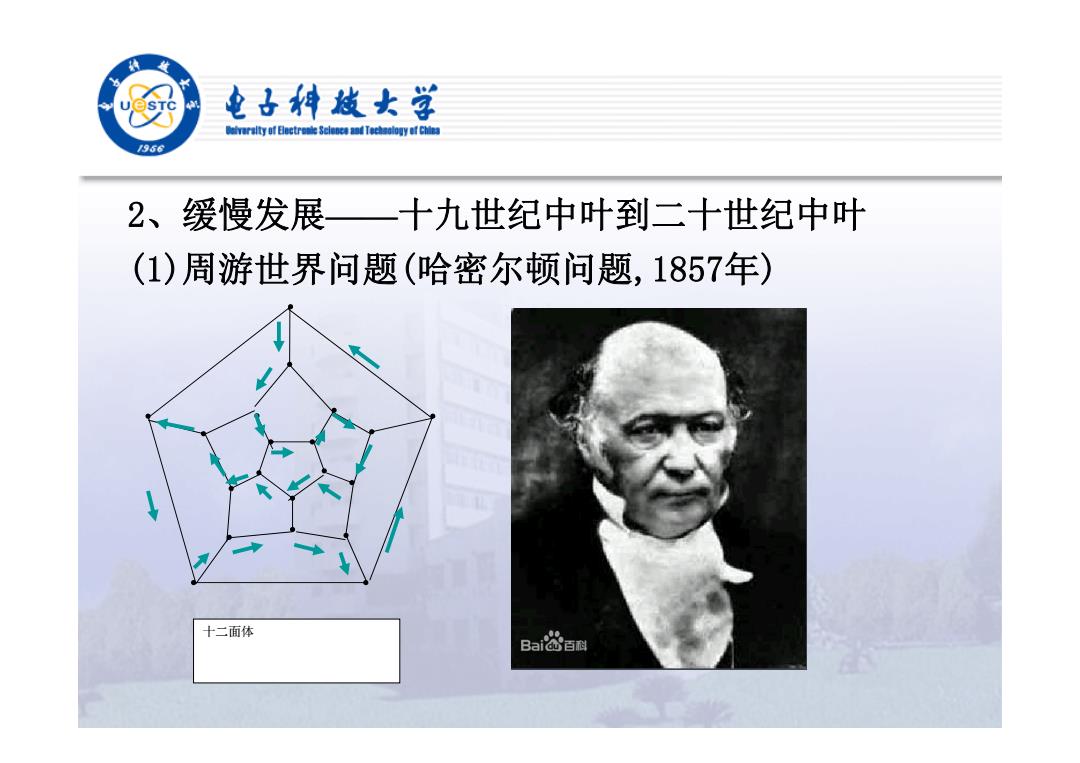
电子科越女学 r街y时Bectrele8 ciad Tecaology af Chins /9568 2、缓慢发展一 十九世纪中叶到二十世纪中叶 (1)周游世界问题(哈密尔顿问题,1857年) 十二面体 Ba&圈
2、缓慢发展——十九世纪中叶到二十世纪中叶 (1)周游世界问题(哈密尔顿问题,1857年) 十二面体

电子科越女学 r街y时Bectrele8 cad Tecaology af Chiaa /956 (2)四色问题(地图染色问题,1852年,格斯里) 还有所谓的克希荷夫生成树问题,欧拉多面体问题,图的平面性问题 以及一些组合优化和运筹学等问题
(2)四色问题(地图染色问题,1852年,格斯里) 还有所谓的克希荷夫生成树问题,欧拉多面体问题,图的平面性问题 以及一些组合优化和运筹学等问题

电子科越女学 r街y时Bectrele8 cad Tecaology afCh /956 (3)第一本图论著作(哥尼【匈牙利】,1936年出版) 哥尼在这本书里,总结了当时所有的图论成果。书 名叫《有限图与无限图理论). 3、快速发展—二十世纪中叶至今 经过最近几十年的发展,形成了一门独立学科。其 典型分支包括:结构图论,代数图论,拓扑图论, 网络图论,随机图论和极值图论。 (二)、图论所属学科 图论属于应用数学的一个分支,是研究“点”与 “线”组成的“图形”问题的一门科学
(3)第一本图论著作(哥尼【匈牙利】,1936年出版) 哥尼在这本书里,总结了当时所有的图论成果。书 名叫《有限图与无限图理论). 3、快速发展——二十世纪中叶至今 经过最近几十年的发展,形成了一门独立学科。其 典型分支包括:结构图论,代数图论,拓扑图论, 网络图论,随机图论和极值图论 。 (二)、图论所属学科 图论属于应用数学的一个分支,是研究“点”与 “线”组成的“图形”问题的一门科学

电子科越女学 r街时Bectrele8 cad Tecaology afCh /956 (三)、图论的应用 图论作为应用数学的一个分支,具有广泛的应用性。 图论的应用已经涵盖了人类学、计算机科学、化学、环境保护、非线性 物理、心理学、社会学、交通管理、电信、网络科学以及数学本身等。 据我所知,已经有许多图论应用专著,如: 1、网络图论及其应用科学出版社陈树柏主编 科学出版社 1982. 2、图论在化学中的应用科学出版社 [罗]A.T.巴拉班编 科学出版社1983. 3、图论及其在计算机科学中的应用中国矿业大学出版社周强 1995. 4、图论及其在图像处理中的应用清华大学出版社李艳灵编 2014
(三)、图论的应用 图论作为应用数学的一个分支,具有广泛的应用性。 图论的应用已经涵盖了人类学、计算机科学、化学、环境保护、非线性 物理、心理学、社会学、交通管理、电信、网络科学以及数学本身等。 据我所知,已经有许多图论应用专著,如: 1、网络图论及其应用 科学出版社 陈树柏主编 科学出版社 1982. 2、图论在化学中的应用 科学出版社 [罗] A.T.巴拉班编 科学出版社 1983. 4、图论及其在图像处理中的应用 清华大学出版社 李艳灵编 2014. 3、图论及其在计算机科学中的应用 中国矿业大学出版社 周强 1995

电子科越女学 r街y时Bectrele8 cad Tecaology af Chiaa /956 两件有趣的事情【我记忆中的事】: 1、陈景润谈哥德巴赫猜想 2、杨振宁80年代做过的一件事。 注:1、由于图论应用广泛,所以,我们开设的这门 课程几乎适合我校全体研究生选修(硕士或博士); 2、近年来,该门课程选修人数稳定在2500以上,受 到了学生的喜爱和良好评价; 3、介绍图论的一些基本概念,基本理论以及具有广 泛应用背景的经典图论算法,讲授60学时。 测试2:A重点关注图论理论;B重点关注图论应用
注:1、由于图论应用广泛,所以,我们开设的这门 课程几乎适合我校全体研究生选修(硕士或博士); 2、近年来,该门课程选修人数稳定在2500以上,受 到了学生的喜爱和良好评价; 3、介绍图论的一些基本概念,基本理论以及具有广 泛应用背景的经典图论算法,讲授60学时。 两件有趣的事情【我记忆中的事】: 1、陈景润谈哥德巴赫猜想; 2、杨振宁80年代做过的一件事 。 测试2: A 重点关注图论理论; B 重点关注图论应用

电子科越女学 r街y时Bectrele8 ciad Tecaology af Chins /956 托特1969年写了一首反映图论的诗: 哥尼斯堡的一些市民, “结果就是这样, 漫步在河畔。 岛屿作为顶点, 在普雷格尔河旁, 四个点有奇数度”。 有七座桥相伴。 从哥尼斯堡到哥尼的书, “Euler,我们一起散步吧!” 图论的传说正是如此, 而且越来越精彩 那些市民在召唤。 绽放在密歇根和耶鲁。 “我们在这七座桥上漫步, 经过每座桥仅一次。” “你们做不到”,Euler:大声吼道
托特1969年写了一首反映图论的诗: 哥尼斯堡的一些市民, 漫步在河畔。 在普雷格尔河旁, 有七座桥相伴。 “Euler,我们一起散步吧!” 那些市民在召唤。 “我们在这七座桥上漫步, 经过每座桥仅一次。” “你们做不到”,Euler大声吼道。 “结果就是这样, 岛屿作为顶点, 四个点有奇数度”。 从哥尼斯堡到哥尼的书, 图论的传说正是如此, 而且越来越精彩, 绽放在密歇根和耶鲁

电子科越女学 r街y时Bectrele8 ciad Tecaology af Chins /956 二、图的定义及其相关概念 (一)、什么是图? 1、C,H的两种同分异构表示 用点抽象分子式中的碳原子和氢原子,用边抽象原子间 的化学键。19世纪化学家凯莱用下面的图表示C4H0的两种 同分异构: hh hh hh h h h h h h h
二、图的定义及其相关概念 (一)、什么是图? 1 、 C 4 H10的两种同分异构表示 用点抽象分子式中的碳原子和氢原子,用边抽象原子间 的化学键。19世纪化学家凯莱用下面的图表示 C 4 H10的两种 同分异构: h hh h hhh h h h h hhh h h h h h h

电子科越女学 r街y时Bectrele8 ciad Tecaology af Chins /956 2、仓库和零售店之间的关系表示 令V={w1,W2,W3,1,r2,r3,r4,rs}代表3个仓库和5个零售点; E={w1r1,W1r2,w22,W23,w2r4,w3r3,W3rs}代表每个仓库和每个 零售店间的关联。则这种关系可以表示为: W3 r2 ra r5
2、仓库和零售店之间的关系表示 令V={w1,w2,w3,r1,r2,r3,r4,r5}代表3个仓库和5个零售点; E={w1r1, w1r2, w2r2, w2r3, w2r4, w3r3, w3r5}代表每个仓库和每个 零售店间的关联。则这种关系可以表示为: w1 r1 r2 w2 r3 r4 w3 r5