
电子摊越女学 elveraityaf Bectrole Sclece and Techaology af Chaa 第一章图的基本概念 本次课内容 一、子图的相关概念 二、几种典型的图运算 三、路与连通性
第一章 图的基本概念 本次课内容 一、子图的相关概念 二、几种典型的图运算 三、路与连通性

电子科越女学 elveraity af Beetronle Sclence and Techaelogy af Cha /956 一、子图的相关概念 1、子图的概念 简单地说,图G的任意一非空部分(包括本身)都称为是图G的 的一个子图。定义如下: 定义1如果V(H)三V(G),E(H)sE(G), 且H中边的重数不超过G中对应边的条数,则称H为 G的子图,记为H三G 当 H三G,H≠G时,称H是G的真子图,记为 H
一、子图的相关概念 1、子图的概念 简单地说,图 G的任意一非空部分 (包括本身 )都称为是图 G 的 的一个子图。定义如下: 定义1 如果 , 且H中边的重数不超过G中对应边的条数,则称H为 G的子图,记为 。 当 时,称H是G的真子图,记为
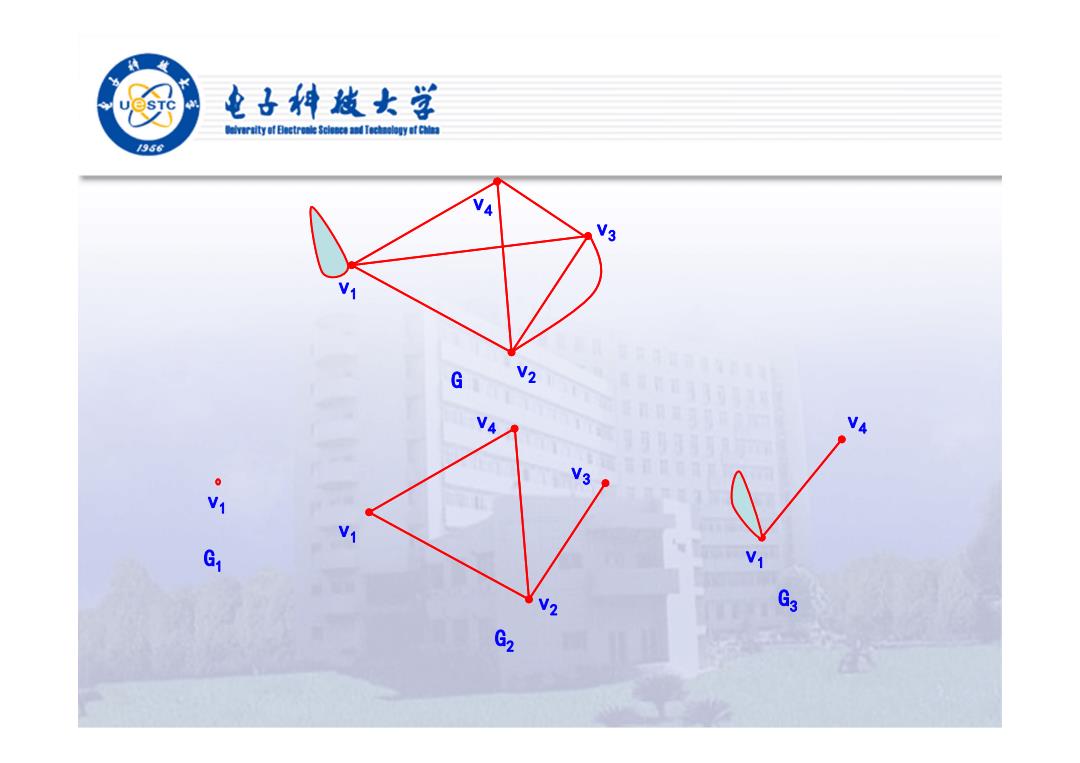
电子特越女学 veraitya Bectrole Sclece and TechaologyafChaa 1956 N3 N G V2 0 v3 V1 G1 69 G2
v 4 v 3 v 2 v1 v 4 v1 v 3 v 2 G 2 v1 G1 v1 v 4 G 3 G
电子摊越女学 elveraity af Beetronle Sclence and Techaelogy af Cha 1956 2、点与边的导出子图 ()图G的顶点导出子图 定义2如果V'三V(G),则以V为顶点集, 以两个端点均在V刀中的边集组成的图,称为 图G的点导出子图。记为:G[V门 例1如图所示,取P'={1,3,5},求G[]. 2 5 3 3 图G GIV']
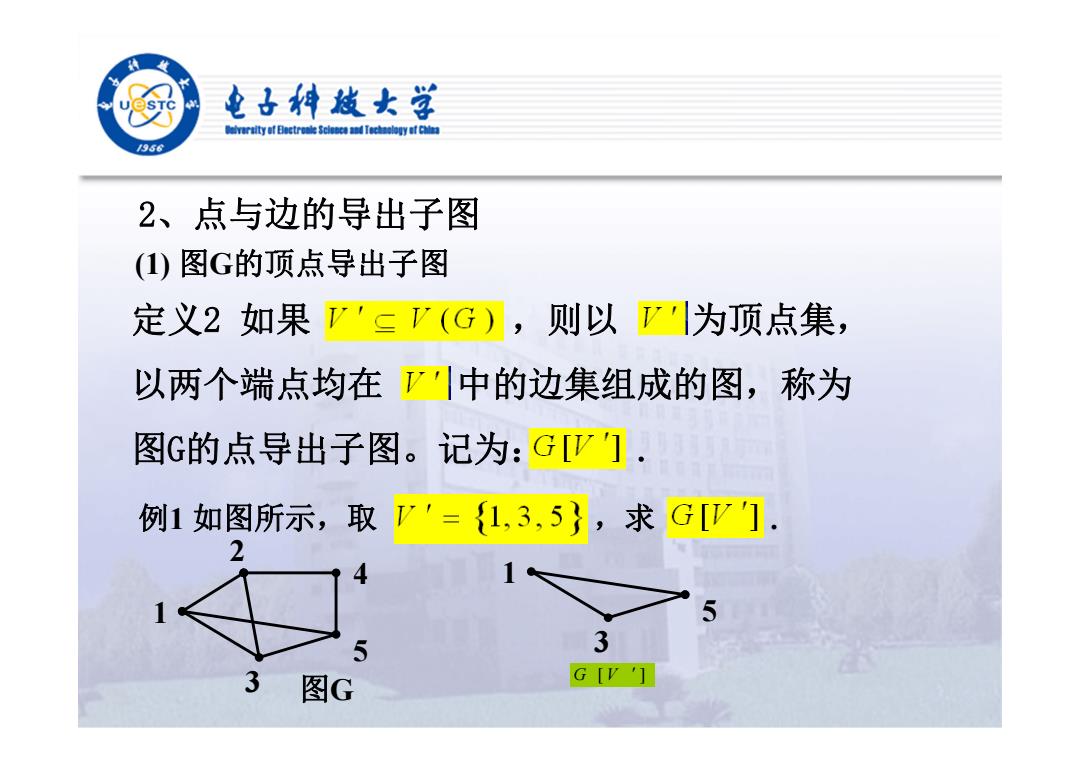
2、点与边的导出子图 (1) 图 G的顶点导出子图 定义2 如果 ,则以 为顶点集, 以两个端点均在 中的边集组成的图,称为 图G的点导出子图。记为: . 例1 如图所示,取 ,求 . 1 2 3 4 5 图 G G V[ ] 1 3 5
ST 电子摊越女学 elveraity af Beetronle Sclence and Techaelogy af Cha 1956 (2)图G的边导出子图 定义3如果E'三E(G),则以E'为边集, 以E”中边的所有端点为顶点集组成的图,称为 图G的边导出子图。记为:G[ET. 例2如图所示,求G[ET。其中E'={13,24,35} 2 5 5 3 图G 3 G[E']
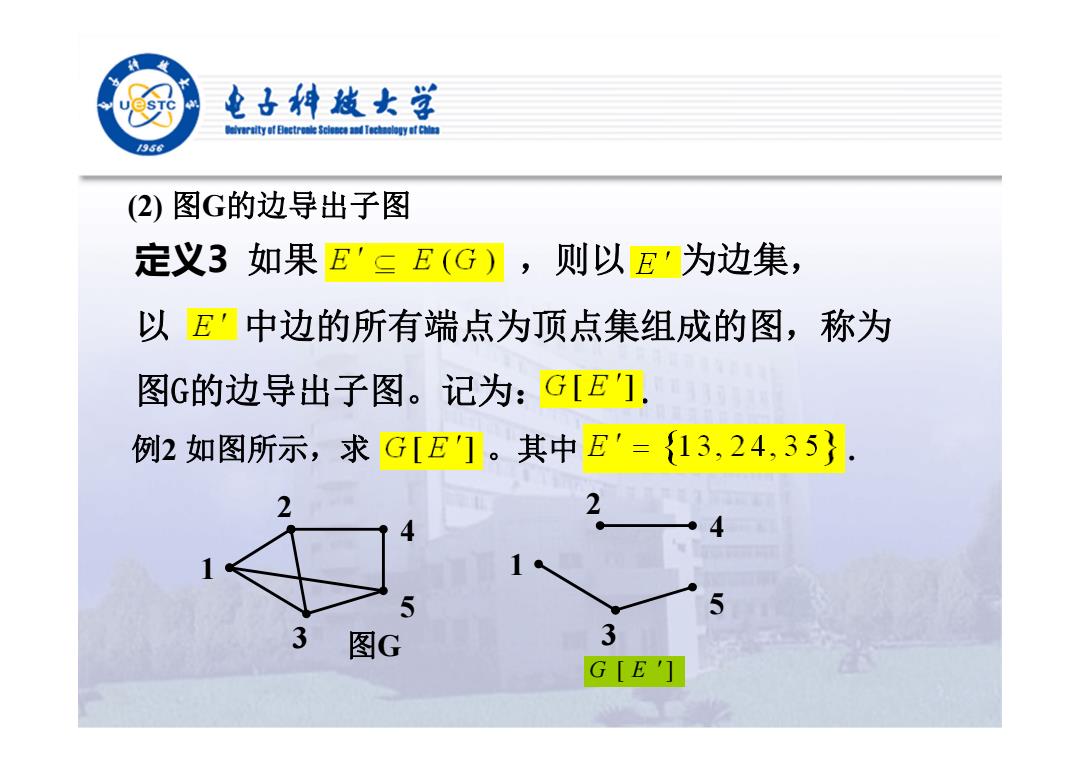
(2) 图G的边导出子图 定义3 如果 ,则以 为边集, 以 中边的所有端点为顶点集组成的图,称为 图G的边导出子图。记为: . 例2 如图所示,求 。其中 . 1 2 3 4 5 图G G E[ ] 1 2 3 4 5
电子摊越女学 elveraity af Beetronle Sclence and Techaelogy af Cha /936 3、图的生成子图 定义3如果图G的一个子图包含G的所有顶点,称 该子图为G的一个生成子图。 例2如图所示,求G的所有生成子图。 ò3 解:按边数分别求出: 图G 。一
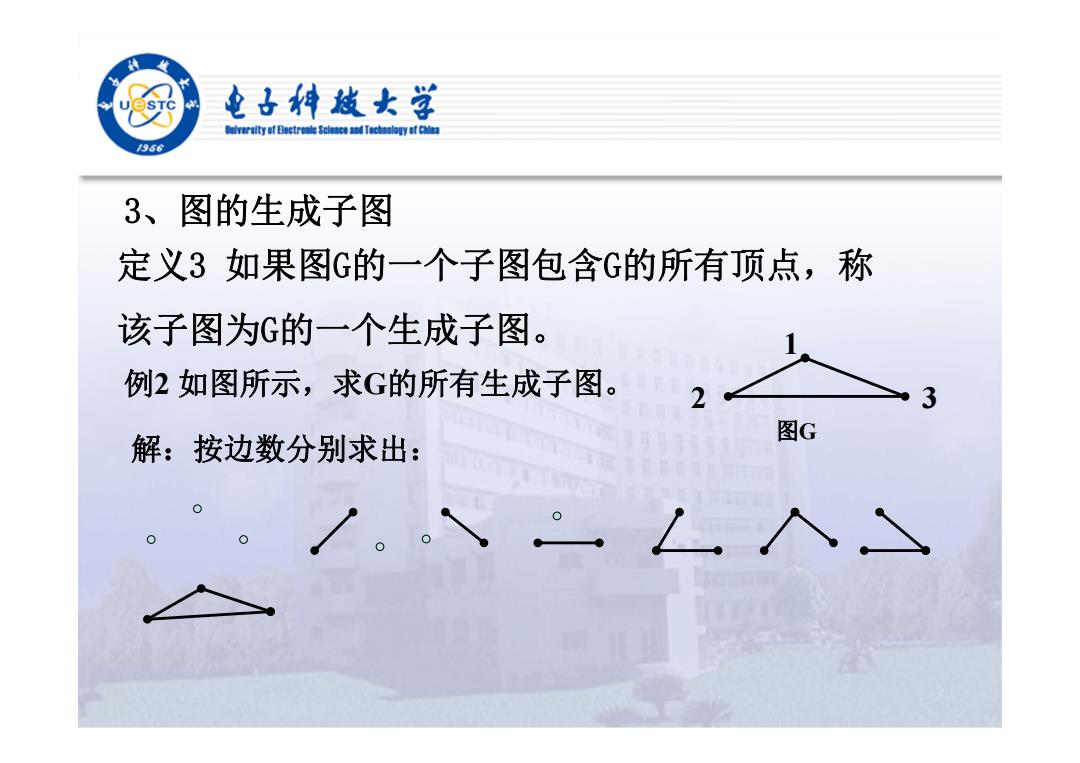
3、图的生成子图 定义3 如果图G的一个子图包含G的所有顶点,称 该子图为G的一个生成子图。 例2 如图所示,求G的所有生成子图。 1 2 3 图G 解:按边数分别求出:

电子摊越女学 elveraity af Beetronle Sclence and Techaelogy af Cha /956 定理1简单图G=(n,m)的所有生成子图个数为2m. 二、图运算 在图论中,将两个或更多的图按照某种方式合并,或者对 一个图作某种形式的操作,可以得到很有意义的新图。将图 合并或对一个图进行操作,称为图运算。图运算形式很多。 (一)、图的删点、删边运算 设V'三V(G), 在G中删去V"中的顶点和G中与之关联 的所有边的操作, 称为删点运算。记为G-P. 特别地,如果只删去一个点v,则记为G-V
定理1 简单图G=(n, m) 的所有生成子图个数为2m. 二、图运算 在图论中,将两个或更多的图按照某种方式合并,或者对 一个图作某种形式的操作,可以得到很有意义的新图。将图 合并或对一个图进行操作,称为图运算。图运算形式很多。 (一)、图的删点、删边运算 设 ,在G中删去 中的顶点和G中与之关联 的所有边的操作,称为删点运算。记为 . 特别地,如果只删去一个点v,则记为G-v
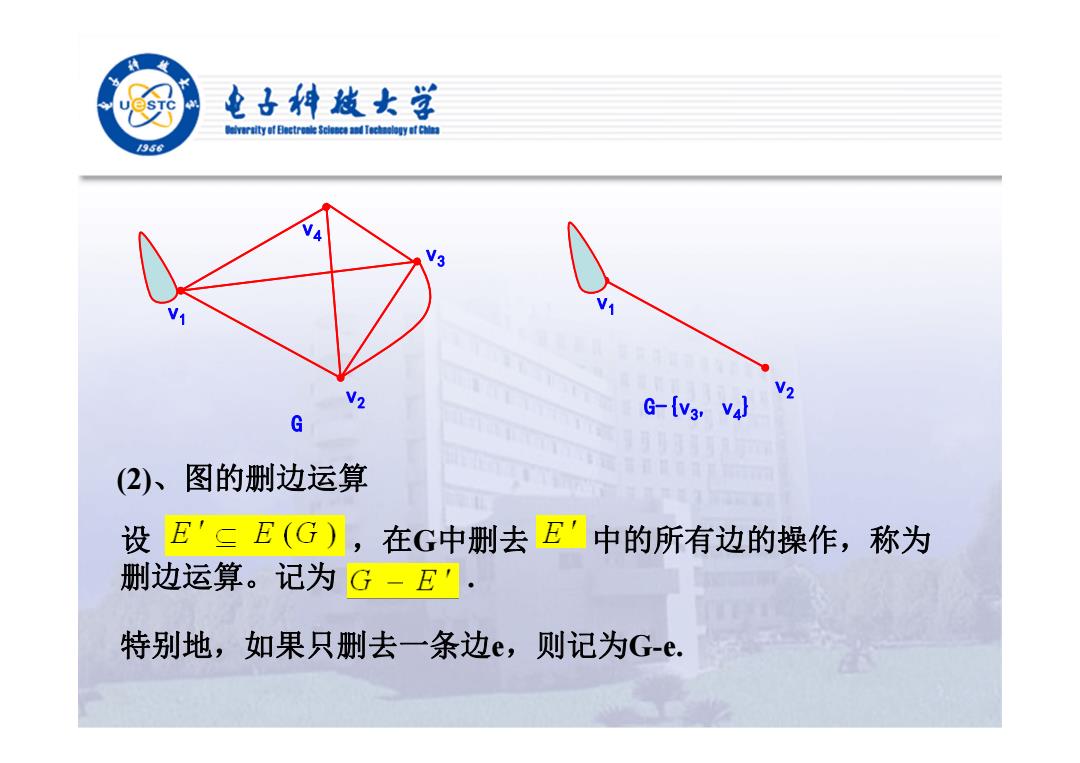
电子特越女学 elveraityaf Bectrole Sclece and Techaology af Chaa /936 V2 V2 G G-[v3,V4] (2)、图的删边运算 设E'三E(G),在G中删去 E'中的所有边的操作,称为 删边运算。记为G一E'· 特别地,如果只删去一条边e,则记为G-e
v4 v3 v2 v1 G v2 v1 G-{v3, v4} (2)、图的删边运算 设 ,在G中删去 中的所有边的操作,称为 删边运算。记为 . 特别地,如果只删去一条边e,则记为G-e

电子摊越女学 elveraityaf Bectrole Sclece and Techaology af Chaa 1956 e VA 。N4 c c 3 e6 es E5 G G-[e1,eg,e6,e5] 注:删点要删关联的边, 删边不删关联的点! (二)、图的并运算 设G,G2是G的两个子图,G,与G,并是指由V(G1)UV(G2)为顶 点集,以E(G1)UE(G2)为边集组成的子图。记为:G1UG2
v1 v2 v3 v4 e1 e2 e3 e4 e5 e6 G G-{ e1, e3, e6, e5 } v1 v2 v3 v4 e2 e4 注:删点要删关联的边,删边不删关联的点! (二)、图的并运算 设G1,G2是G的两个子图,G1与G2并是指由 为顶 点集,以 为边集组成的子图。记为:
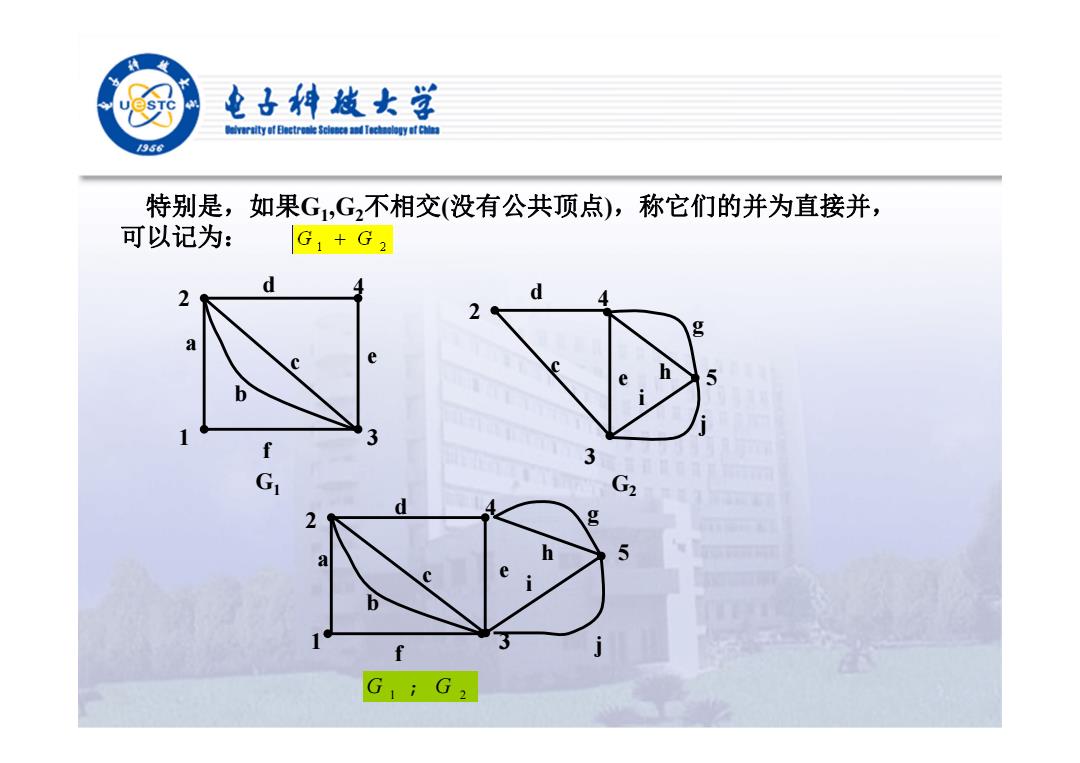
电子科越女学 elveraityaf Bectrole Sclece and Techaology af Chaa 1956 特别是,如果G,G,不相交(没有公共顶点), 称它们的并为直接并, 可以记为: G1+G2 d d a e 3 f 3 G2 d 2 h a G1;G2
特别是,如果G1,G2不相交(没有公共顶点),称它们的并为直接并, 可以记为: . 1 2 3 4 a b c d e f G1 h 2 3 5 4 c d e g i j G2 1 2 3 4 a b c d e f h 5 g i j G G 1 2 U