
之 本次课主要内容 割边、割点和块 (一)、割边及其性质 (二)、割点及其性质 (三)、块及其性质
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 本次课主要内容 (一)、割边及其性质 (二)、割点及其性质 (三)、块及其性质 割边、割点和块

研究图的连通性的意义 研究图的连通性,主要研究图的连通程度的刻画, 其意义是: 图论意义:图的连通程度的高低,是图结构性质的重 要表征,图的许多性质都与其相关,例如:连通图中任 意两点间不相交路的条数就与图的连通程度有关。 实际意义:图的连通程度的高低,对应于通信网络 “可靠性程度”的高低。 (一)、割边及其性质 定义1边e为图G的一条割边, 如果 @(G-e)>@(G) 红色边为该图的割边
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 研究图的连通性的意义 研究图的连通性,主要研究图的连通程度的刻画, 其意义是: 图论意义:图的连通程度的高低,是图结构性质的重 要表征,图的许多性质都与其相关,例如:连通图中任 意两点间不相交路的条数就与图的连通程度有关。 实际意义:图的连通程度的高低,对应于通信网络 “可靠性程度”的高低。 (一)、割边及其性质 定义1 边e为图G的一条割边,如果 。 ( ) () Ge G 红色边为该图的割边

注:割边又称为图的“桥 图的割边有如下性质: 定理1边e是图G的割边当且仅当e不在G的任何圈中。 证明:可以假设G连通。 “必要性” 若不然。设e在图G的某圈C中,且令e=uv. 考虑P=C-e,则P是一条uv路。下面证明G-e连通。 对任意x,y∈V(G-e),由于G连通,所以存在x-y 路Q.若Q不含e,则x与y在G-e里连通;若Q含有e,则可 选择路:x--uPv--y,说明x与y在G-e里也连通。所以, 若边e在G的某圈中,则G-e连通。 但这与e是G的割边矛盾!
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 注:割边又称为图的“桥”。 图的割边有如下性质: 定理1 边 e 是图G的割边当且仅当 e 不在G的任何圈中。 证明:可以假设G连通。 若不然。设 e 在图G的某圈 C 中,且令e = u v. 考虑P = C- e,则P是一条u v路。下面证明G-e连通。 对任意 x, y V(G-e) ,由于G连通,所以存在x ---y 路Q.若Q不含e,则x与y在G-e里连通;若Q含有e,则可 选择路:x ---u P v --- y,说明x与y在G-e里也连通。所以, 若边e在G的某圈中,则G-e连通。 但这与e是G的割边矛盾! “必要性

“充分性” 如果e不是G的割边,则G-e连通,于是在G-e中存在 一条u-v路,显然:该路并上边e得到G中一个包含边 e的圈,矛盾。 推论1e为连通图G的一条边,如果e含于G的某圈中, 则G-e连通。 证明:若不然,G-e不连通,于是e是割边。由定理1, e不在G的任意圈中,矛盾! 例1求证:(1)若G的每个顶点的度数均为偶数,则G 没有割边;(2)若G为k正则二部图k≥2),则G无割边。 证明:(I)若不然,设e=uv为G的割边。则Ge的含有 顶点u(或v)的那个分支中点u(或v)的度数为奇,而其余点 的度数为偶数,与握手定理推论相矛盾!
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 “充分性” 如果e不是G的割边,则G-e连通,于是在G-e中存在 一条u --- v 路,显然:该路并上边e得到G中一个包含边 e的圈,矛盾。 推论1 e为连通图G的一条边,如果e含于G的某圈中, 则G-e连通。 证明:若不然,G-e不连通,于是e是割边。由定理1, e不在G的任意圈中,矛盾! 例1 求证: (1) 若G的每个顶点的度数均为偶数,则G 没有割边; (2) 若G为k正则二部图(k≧2),则G无割边。 证明: (1)若不然,设e=uv 为G的割边。则G-e的含有 顶点u(或v)的那个分支中点u(或v)的度数为奇,而其余点 的度数为偶数,与握手定理推论相矛盾!

(2)若不然,设e=uv为G的割边。取G-e的其中一个分 支G1,显然,G,中只有一个顶点的度数是k-1,其余点的度 数为k。并且G,仍然为偶图。 假若G,的两个顶点子集包含的顶点数分别为m与n,并且 包含m个顶点的顶点子集包含度为k-1的那个点,那么有: km-1=kn。但是因k≥2,所以等式不能成立!
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 (2)若不然,设e=uv 为G的割边。取G-e的其中一个分 支G1, 显然,G1中只有一个顶点的度数是k-1,其余点的度 数为k。并且G1仍然为偶图。 假若G1的两个顶点子集包含的顶点数分别为m与n,并且 包含m个顶点的顶点子集包含度为k-1的那个点,那么有: k m – 1 = k n。但是因k≧2,所以等式不能成立!
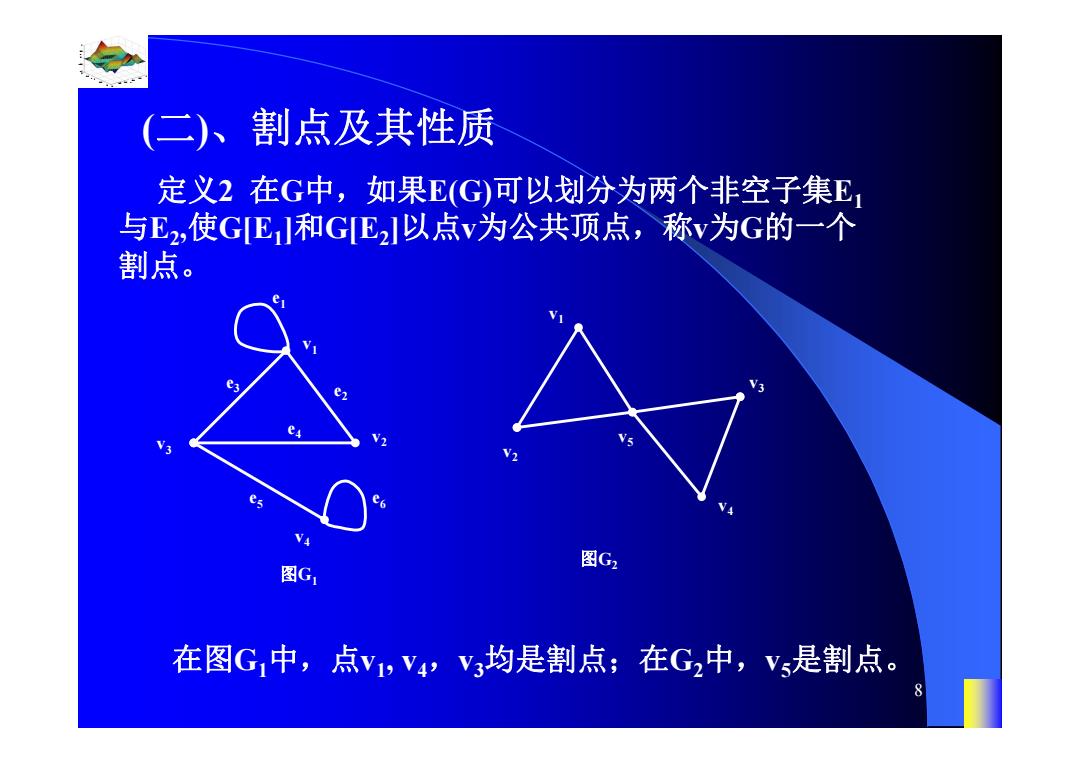
(二)、割点及其性质 定义2在G中,如果E(G)可以划分为两个非空子集E, 与E2,使GE]和GE以点v为公共顶点,称v为G的一个 割点。 图G2 图G, 在图G,中,点v1,V4V均是割点;在G2中,Vs是割点。 8
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 (二)、割点及其性质 定义2 在G中,如果E(G)可以划分为两个非空子集E1 与E2,使G[E1]和G[E2]以点v为公共顶点,称v为G的一个 割点。 v1 v v2 3 v4 e3 e1 e2 e4 e5 e6 图G1 v1 v3 v2 v4 v5 图G2 在图G1中,点v1, v4,v3均是割点;在G2中,v5是割点

定理2G无环且非平凡,则v是G的割点,当且仅当 @(G-v)>@(G) 证明:“必要性” 设v是G的割点。则E(G可划分为两个非空边子集E, 与E2,使GE,l,GE2恰好以v为公共点。 由于G没有环,所以,GE,GE分别至少包含异于v的 G的点,这样,G-v的分支数比G的分支数至少多1,所以: @(G-v)>@(G)
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 定理2 G无环且非平凡,则v是G的割点,当且仅当 ( ) () Gv G 证明:“必要性” 设v是G的割点。则E(G)可划分为两个非空边子集E1 与E2,使G[E1],G[E2]恰好以v为公共点。 由于G没有环,所以,G[E1],G[E2]分别至少包含异于v的 G的点,这样,G-v的分支数比G的分支数至少多1,所以: ( ) () Gv G

“充分性” 由割点定义结论显然。 定理3v是树T的顶点,则v是割点, 当且仅当是树 的分支点。 证明:“必要性” 若不然,有d(=1,即v是树叶,显然不能是割点。 “充分性” 设是分支点,则d(>1.于是设x与y是v的邻点,由树 的性质,只有唯一路连接x与y,所以G-v分离x与y.即v为 割点。 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 “充分性” 由割点定义结论显然。 定理3 v 是树T的顶点,则v是割点,当且仅当v是树 的分支点。 证明:“必要性” 若不然,有d (v)=1,即v是树叶,显然不能是割点。 “充分性” 设v是分支点,则d (v)>1.于是设x与y是v的邻点,由树 的性质,只有唯一路连接x与y,所以G-v分离x与y .即v为 割点

定理4设是无环连通图G的一个顶点,则v是G的割 点,当且仅当V(G-)可以划分为两个非空子集V与V,使 得对任意x∈V,y∈V,点在每一条xy路上。 证明:“必要性” v是无环连通图G的割点,由定理2,G-v至少有两个 连通分支。设其中一个连通分支顶点集合为V,另外分支 顶点集合为V,即V与V构成V的划分。 对于任意的x∈V,y∈Y,如果点v不在某一条xy路 上,那么,该路也是连接G-v中的x与的路,这与x,y处 于G-的不同分支矛盾。 “充分性” 若v不是图G的割点,那么G-连通,因此在G-v中存在 x,y路,当然也是G中一条没有经过点v的x,y路。矛盾
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 定理4 设v是无环连通图G的一个顶点,则v是G的割 点,当且仅当V(G-v)可以划分为两个非空子集V1与V2,使 得对任意x ∈V1, y ∈V2, 点v在每一条x y路上。 证明:“必要性” v是无环连通图G的割点,由定理2,G-v至少有两个 连通分支。设其中一个连通分支顶点集合为V1, 另外分支 顶点集合为V2,即V1与V2构成V的划分。 “充分性” 对于任意的x ∈V1, y ∈V2,如果点v不在某一条x y路 上,那么,该路也是连接G-v中的x与y的路,这与x, y处 于G-v的不同分支矛盾。 若v不是图G的割点,那么G-v连通,因此在G-v中存在 x, y路,当然也是G中一条没有经过点 v 的x, y路。矛盾

例2求证:无环非平凡连通图至少有两个非割点。 证明: 由于G是无环非平凡连通图,所以存在非平 凡生成树,而非平凡生成树至少两片树叶,它不能为割 点,所以,它也不能为G的割点。 例3求证:恰有两个非割点的连通单图是一条路。 证明:设T是G的一棵生成树。由于G有-2个割点, 所以,T有-2个割点,即T只有两片树叶,所以T是一条 路。这说明,G的任意生成树为路。 一个单图的任意生成树为路,则该图为圈或路,若为 圈,则G没有割点,矛盾,所以,G为路。 例4求证:若v是单图G的割点,则它不是G的补图的 割点
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 12 例2 求证:无环非平凡连通图至少有两个非割点。 证明: 由于G是无环非平凡连通图,所以存在非平 凡生成树,而非平凡生成树至少两片树叶,它不能为割 点,所以,它也不能为G的割点。 证明:设T是G的一棵生成树。由于G有n-2个割点, 所以,T有n-2个割点,即T只有两片树叶,所以T是一条 路。这说明,G的任意生成树为路。 例3 求证:恰有两个非割点的连通单图是一条路。 一个单图的任意生成树为路,则该图为圈或路,若为 圈,则G没有割点,矛盾,所以,G为路。 例4 求证:若v是单图G的割点,则它不是G的补图的 割点