
本次课主要内容 图的顶点着色 (一)、相关概念 (二)、图的点色数的几个结论 (三)、四色与五色定理 (四)、顶点着色的应用
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (一)、相关概念 (二)、图的点色数的几个结论 (三)、四色与五色定理 图的顶点着色 (四)、顶点着色的应用

(一)、相关概念 跟图的边着色问题一样,生活中的很多问题,也可以 模型为所谓的图的顶点着色问题来处理。例如课程安排 问题。 课程安排问题:某大学数学系要为这个夏季安排课程 表。所要开设的课程为:图论(GT),统计学(S),线性代数 LA),高等微积分(AC),几何学(G),和近世代数MA)。现 有10名学生(如下所示)需要选修这些课程。根据这些信息, 确定开设这些课程所需要的最少时间段数,使得学生选 课不会发生冲突。(学生用A表示) A:LA,S;A2:MA,LA,G;A3:MA,G,LA; A:G,LA,AC;As:AC,LA,S;A:G,AC; Az:GT,MA,LA;As:LA,GT,S;A:AC,S,LA;A10:GT,S
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 跟图的边着色问题一样,生活中的很多问题,也可以 模型为所谓的图的顶点着色问题来处理。例如课程安排 问题。 (一)、相关概念 课程安排问题:某大学数学系要为这个夏季安排课程 表。所要开设的课程为:图论(GT), 统计学(S),线性代数 (LA), 高等微积分(AC), 几何学(G), 和近世代数(MA)。现 有10名学生(如下所示)需要选修这些课程。根据这些信息, 确定开设这些课程所需要的最少时间段数,使得学生选 课不会发生冲突。(学生用Ai表示) A1: LA, S ; A2: MA, LA, G ; A3: MA, G, LA; A4: G, LA, AC ; A5: AC, LA, S ; A6: G, AC; A7: GT, MA, LA ; A8: LA,GT, S ; A9: AC, S, LA; A10: GT, S

把课程模型为图G的顶点,两顶点连线当且仅当有某 个学生同时选了这两门课程。 GT MA AC 选课状态图
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 把课程模型为图G的顶点,两顶点连线当且仅当有某 个学生同时选了这两门课程。 GT MA G AC LA S 选课状态图
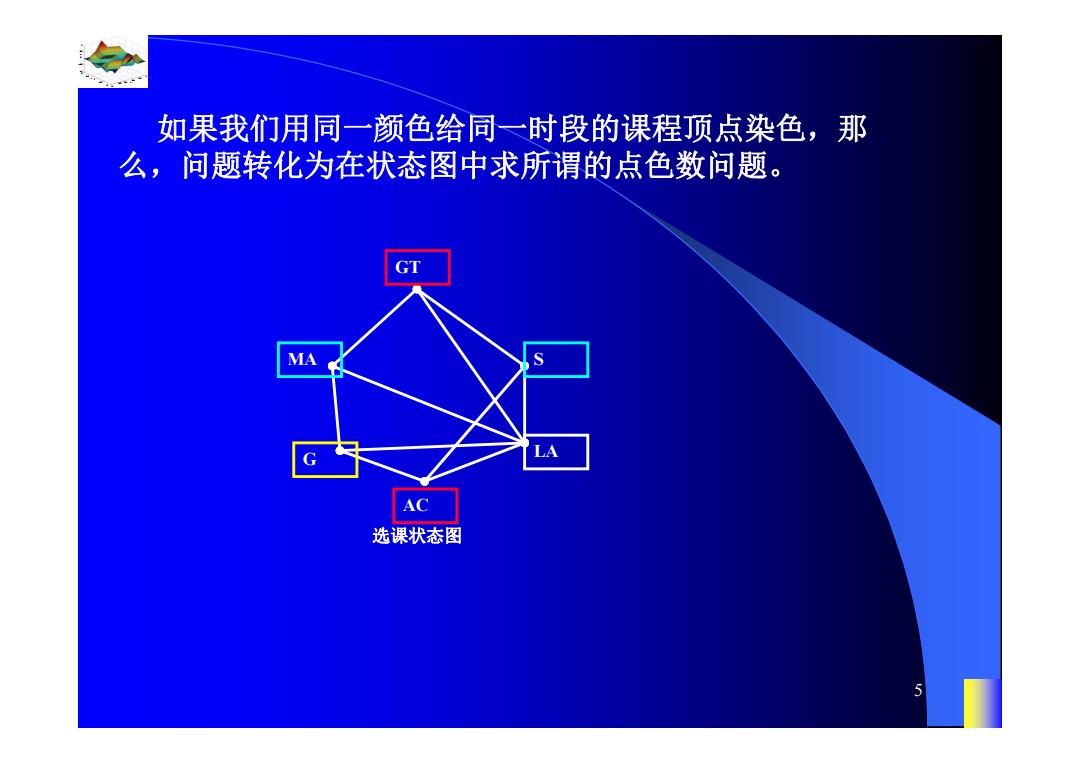
如果我们用同一颜色给同二时段的课程顶点染色,那 么,问题转化为在状态图中求所谓的点色数问题。 GT MA LA AC 选课状态图
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 如果我们用同一颜色给同一时段的课程顶点染色,那 么,问题转化为在状态图中求所谓的点色数问题。 GT MA G AC LA S 选课状态图
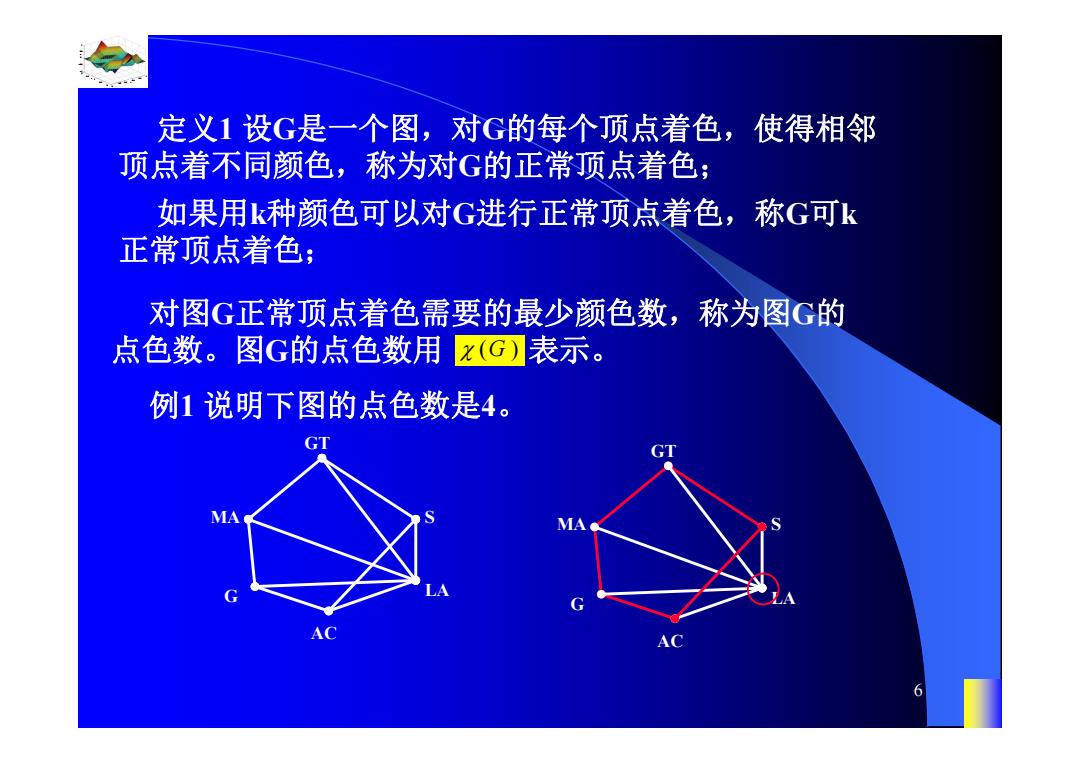
定义1设G是一个图,对G的每个顶点着色,使得相邻 顶点着不同颜色,称为对G的正常顶点着色; 如果用k种颜色可以对G进行正常顶点着色,称G可k 正常顶点着色; 对图G正常顶点着色需要的最少颜色数,称为图G的 点色数。图G的点色数用 x(G)表示。 例1说明下图的点色数是4。 GT GT AC 6
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 定义1 设G是一个图,对G的每个顶点着色,使得相邻 顶点着不同颜色,称为对G的正常顶点着色; 如果用k种颜色可以对G进行正常顶点着色,称G可k 正常顶点着色; 对图G正常顶点着色需要的最少颜色数,称为图G的 点色数。图G的点色数用 表示。 ( ) G 例1 说明下图的点色数是4。 GT MA G AC LA S GT MA G AC LA S
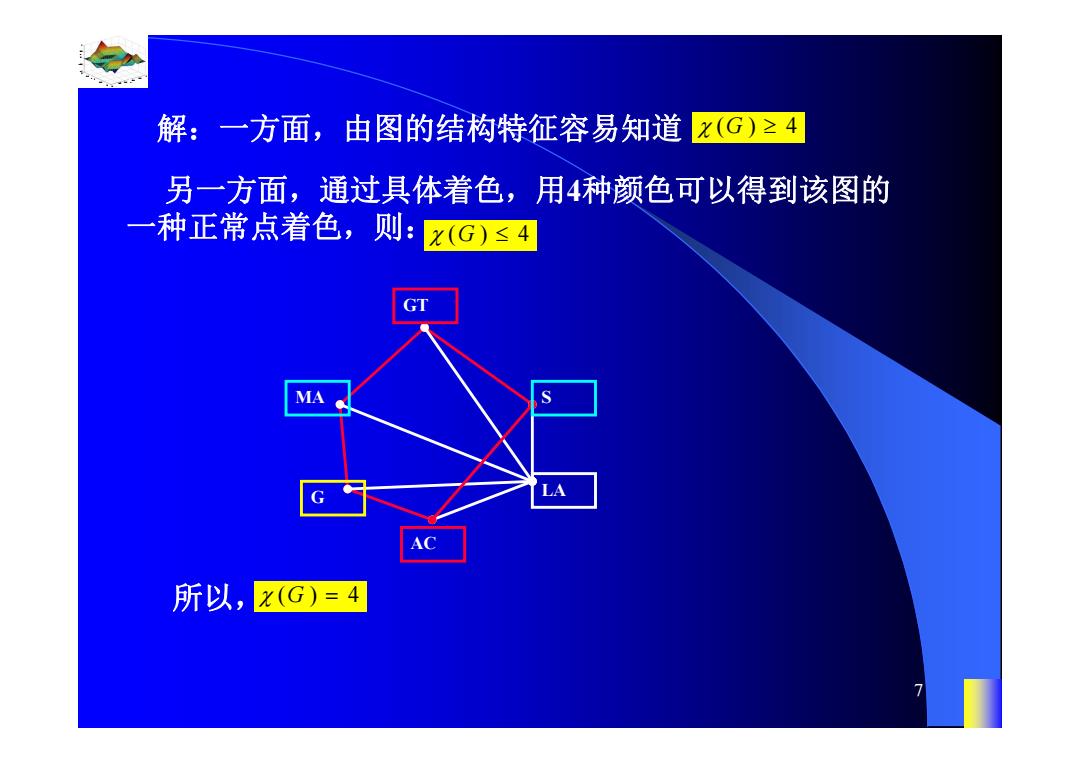
解:一方面,由图的结构特征容易知道 x(G)≥4 另一方面,通过具体着色,用4种颜色可以得到该图的 种正常点着色,则: x(G)≤4 GT MA LA AC 所以,(G)=4
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 解:一方面,由图的结构特征容易知道 () 4 G 另一方面,通过具体着色,用4种颜色可以得到该图的 一种正常点着色,则: () 4 G GT MA G AC LA S 所以, () 4 G

注:对图的正常顶点着色,带来的是图的顶点集合的 种划分方式。所以,对应的实际问题也是分类问题。属 于同一种颜色的顶点集合称为一个色组,它们彼此不相 邻接,所以又称为点独立集。用点色数种颜色对图G正常 着色,称为对图G的最优点着色。 定义2 色数为k的图称为k色图。 (二)、图的点色数的几个结论 定理1对任意的图G,有:(G)≤△(G)+1 分析:事实上,定理结论容易想到,因为任意一个顶点 度数至多为△,因此,正常着色过程中,其邻点最多用去△ 种颜色,所以,至少还有一种色可供该点正常着色使用
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 注:对图的正常顶点着色,带来的是图的顶点集合的一 种划分方式。所以,对应的实际问题也是分类问题。属 于同一种颜色的顶点集合称为一个色组,它们彼此不相 邻接,所以又称为点独立集。用点色数种颜色对图G正常 着色,称为对图G的最优点着色。 定义2 色数为k的图称为k色图。 (二)、图的点色数的几个结论 定理1 对任意的图G,有: () ()1 G G 分析:事实上,定理结论容易想到,因为任意一个顶点 度数至多为Δ,因此,正常着色过程中,其邻点最多用去Δ 种颜色,所以,至少还有一种色可供该点正常着色使用

证明:我们对顶点数作数学归纳证明。 当=1时,结论显然成立。 设对顶点数少于的图来说,定理结论成立。考虑一般 的n阶图G。 任取v∈V(G),令G,=G-v,由归纳假设: x(G)≤△(G)+1≤△(G)+1 设Π是G,的一种△(G)+1正常点着色方案,因为v的邻点 在Ⅱ下至多用去△(G)种色,所以给v染上其邻点没有用过 的色,就把m扩充成了G的△(G)+1着色方案。 对于G来说,可以给出其△(G)+1正常点着色算法
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 证明:我们对顶点数作数学归纳证明。 当n=1时,结论显然成立。 设对顶点数少于n的图来说,定理结论成立。考虑一般 的n阶图G。 任取v ∈V(G), 令G1=G-v, 由归纳假设: 1 1 ( ) ( )1 ()1 GG G 设п是G1的一种Δ(G)+1正常点着色方案,因为v的邻点 在п下至多用去Δ(G)种色,所以给v染上其邻点没有用过 的色,就把п扩充成了G的Δ(G)+1着色方案。 对于G来说,可以给出其Δ(G)+1正常点着色算法

G的△(G)+1正常点着色算法 设G=(VE),V={v1Y2Vn},色集合C={1,2,,△+1}, 着色方案为Π。 (1)令Π(v)=1,i=1; (2)若i=n,则停止;否则令: C(心)={π(y,)≤i,并且y,与y相邻 设k为C-C(y+1)中的最小整数,令x(y)=k (3)令i=i+1,转(2)。 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 G的Δ(G)+1正常点着色算法 设G=(V, E), V={v1,v2,…,vn},色集合C={1,2,…,Δ+1}, 着色方案为п。 (1) 令п(v1)=1, i=1; (2) 若i=n,则停止;否则令: Cv v j i v v ( ) () , i j ji 1 1 并且 与 相邻 设k为C-C(vi+1)中的最小整数,令 +1 ( )= i v k (3) 令i=i+1,转(2)

例2给出下图的△+1正常点着色。 解:色集C={1,2,3,4,5} (1),π(y1)=1 (2),C(v2)={1,C-C(y2)={2,3,4,5},k=2 (1),π(y2)=2 (2),C(3)={1,2},C-C(3)={3,4,5},k=3 11
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 例2 给出下图的Δ+1正常点着色。 v5 v4 v3 v2 v1 v6 解:色集C={1, 2, 3, 4, 5} 1 (1), ( )=1 v (2), ( )= 1 , ( ) 2, 3, 4, 5 , 2 Cv C Cv k 2 2 2 (1), ( )=2 v (2), ( )= 1, 2 , ( ) 3, 4, 5 , 3 Cv C Cv k 3 3