
本次课主要内容 着色的计数与色多项式 (一)、色多项式概念 (二)、色多项式的两种求法 (三)、色多项式的性质
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (一)、色多项式概念 (二)、色多项式的两种求法 着色的计数与色多项式 (三)、色多项式的性质

(一)、色多项式概念 所谓色计数,就是给定标定图G和颜色数k,求出正常顶 点着色的方式数。方式数用P(G)表示。 可以证明:P(G)是k的多项式,称为图G的色多项式。 由点色数G和色多项式PG)的定义可得: (1)若 k<z©,则Px(G)=0;2zG)=min{kP.(G)2 (2)若G为空图,则P(G)=k"。 (3)P(K=k(k-1).(k-n+1)
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 所谓色计数,就是给定标定图G和颜色数k,求出正常顶 点着色的方式数。方式数用Pk(G)表示。 ( ) min ( ) 1 G kP G k (一)、色多项式概念 可以证明:Pk(G)是k的多项式,称为图G的色多项式。 由点色数 和色多项式Pk ( ) G (G)的定义可得: (1) 若 ,则Pk k G ( ) (G)=0 ; (2) 若G为空图,则Pk(G)=kn。 (3) Pk(Kn)=k(k-1)…(k-n+1)

(二)、色多项式的两种求法 1、递推计数法 定理1设G为简单图,则对任意 e∈E(G)有: P(G)=P(G-e)-P(Ge) 证明:设e=uv。则对G-e的着色方式数可以分为两部分: (1)u与v着不同颜色。此时,等于G的着色方式数; (2)u与v着同色。此时,等于Ge的着色方式数; 所以,得:P(G)=P(G-e)-P(Ge)
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 1、递推计数法 (二)、色多项式的两种求法 定理1 设G为简单图,则对任意 有: e EG ( ) () ( ) ( ) Pkk k G P G e P Ge 证明:设e=uv。则对G-e的着色方式数可以分为两部分: (1) u与v着不同颜色。此时,等于G的着色方式数; (2) u与v着同色。此时,等于Gꞏe 的着色方式数; 所以,得: () ( ) ( ) Pkk k G P G e P Ge
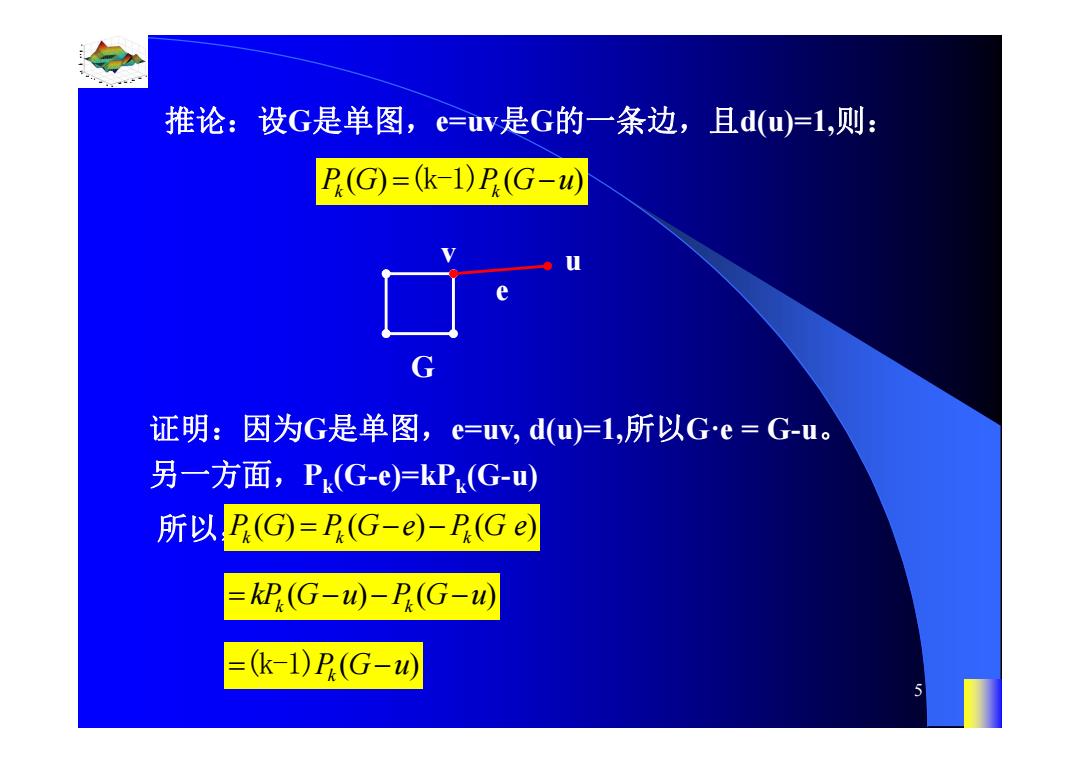
推论:设G是单图,e=v是G的一条边,且d(u=1,则: P(G)=(k-1)P(G-w) 证明:因为G是单图,e=uy,d(u=1,所以Ge=G-u。 另一方面,P(G-e)=kPk(G-u) 所以P(G)=P(G-e)-P(Ge) =P(G-0-P(G-0 =(k-1)P.(G-w
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 推论:设G是单图,e=uv是G的一条边,且d(u)=1,则: 证明:因为G是单图,e=uv, d(u)=1,所以Gꞏe = G-u。 另一方面,Pk(G-e)=kPk(G-u) 所以, () ( ) Pk k G PG u (k-1) () ( ) ( ) Pkk k G P G e P Ge ( )( ) k k kP G u P G u ( ) (k-1)Pk G u u e G v
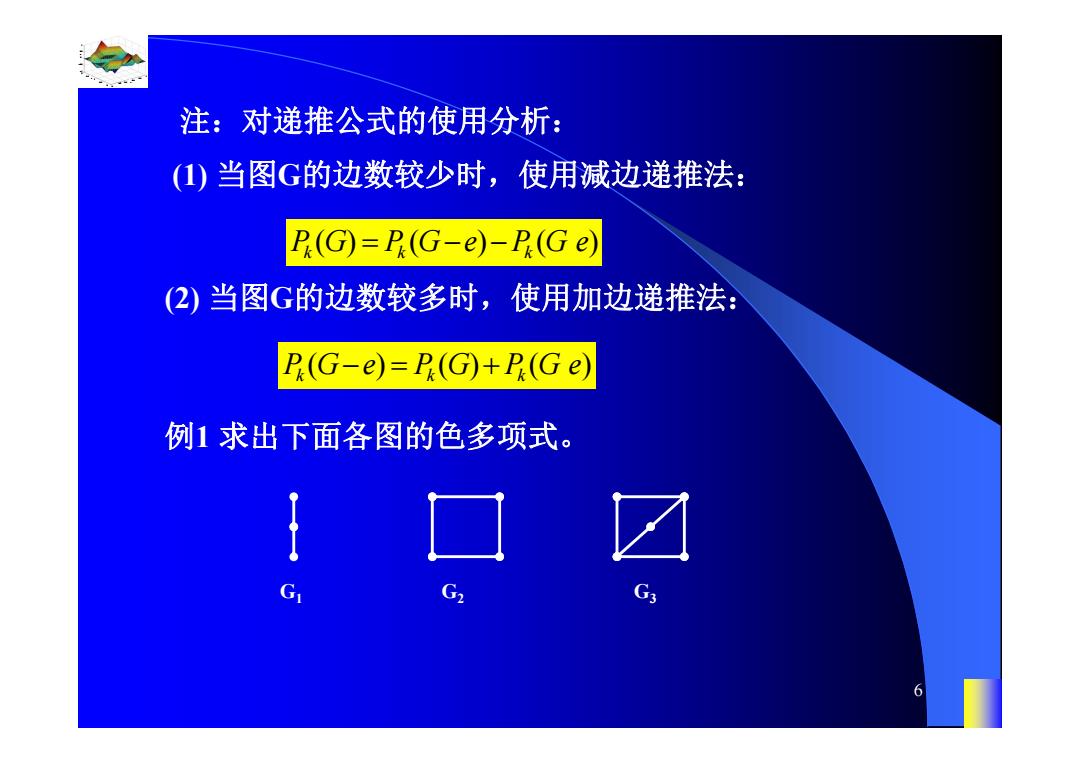
注:对递推公式的使用分析: (1)当图G的边数较少时,使用减边递推法: P(G)=P.(G-e)-P.(Ge) (2)当图G的边数较多时,使用加边递推法: P(G-e)=P(G)+P(Ge) 例1求出下面各图的色多项式。 G 6
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 (1) 当图G的边数较少时,使用减边递推法: () ( ) ( ) Pkk k G P G e P Ge (2) 当图G的边数较多时,使用加边递推法: ( ) () ( ) Pk kk G e P G P Ge 例1 求出下面各图的色多项式。 G1 G2 G3 注:对递推公式的使用分析:
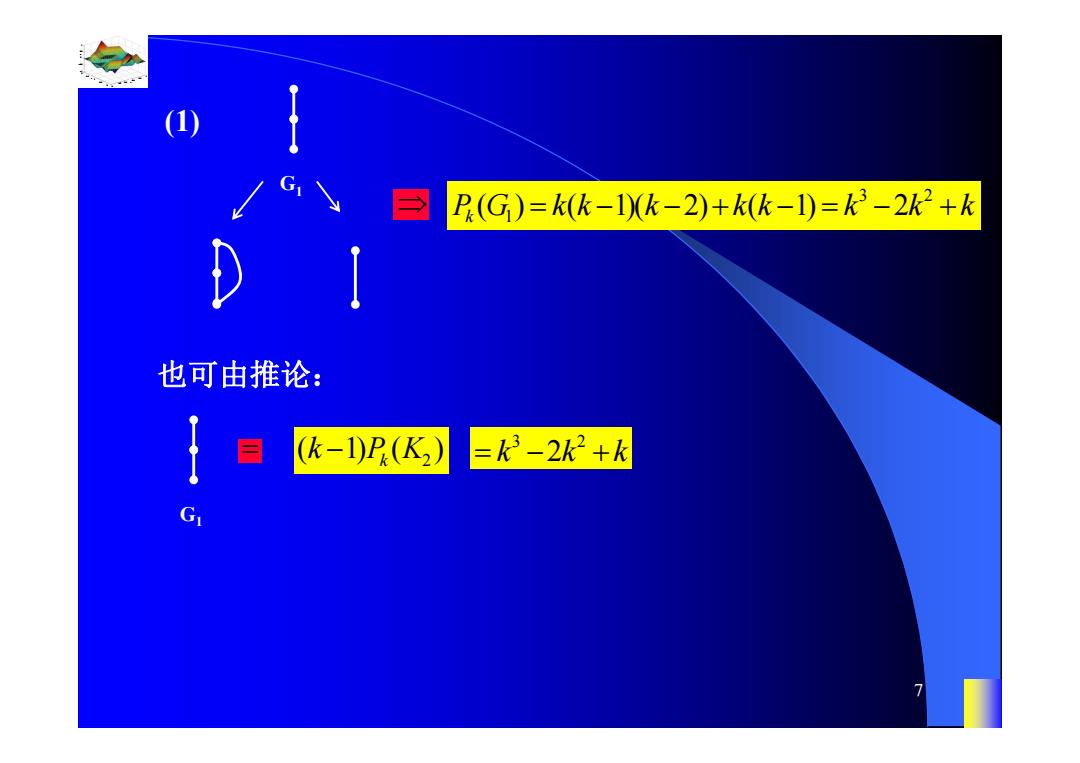
(1 P.(G)=k(k-1k-2)+k(k-1)=k3-2k2+k 也可由推论: (k-1)P(K) =K-2K2+k G
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 (1) G1 3 2 1 Pk ( ) ( 1)( 2) ( 1) 2 G kk k kk k k k 也可由推论: G1 2 ( 1) ( ) k k PK 3 2 k kk 2
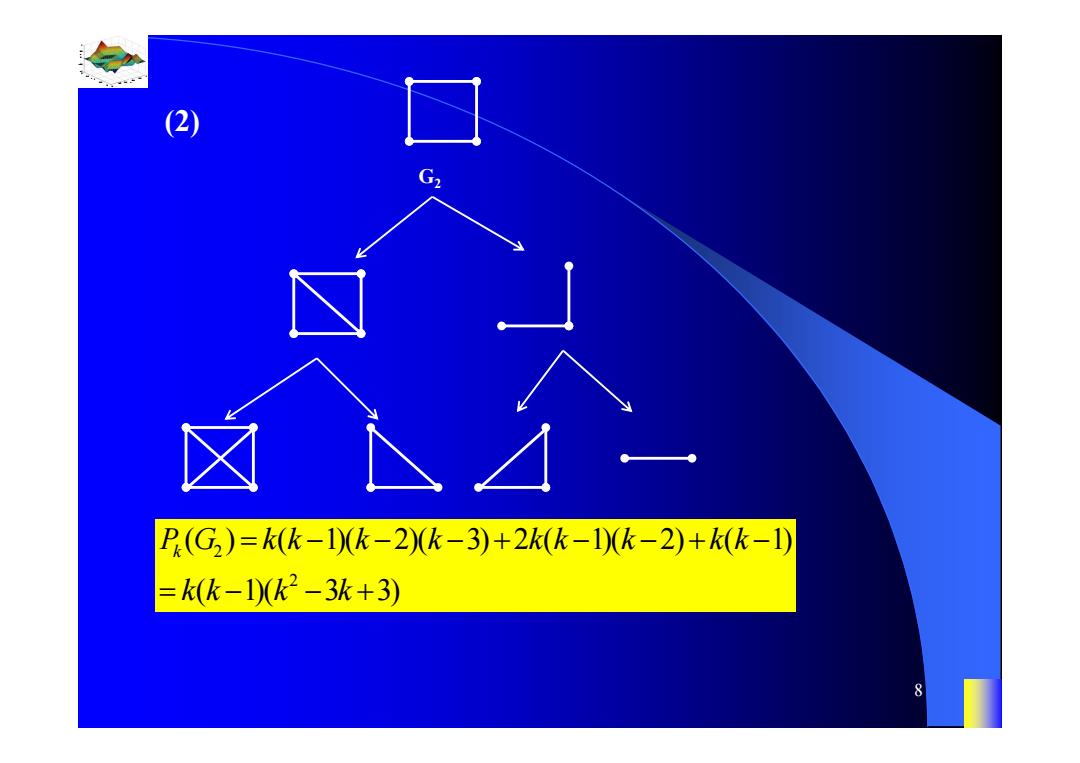
(2) P.(G2)=k(k-1(k-2k-3)+2k(k-1k-2)+k(k-1) =k(k-1)K2-3k+3) 8
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 (2) G2 2 2 ( ) ( 1)( 2)( 3) 2 ( 1)( 2) ( 1) ( 1)( 3 3) PG kk k k kk k kk k kk k k
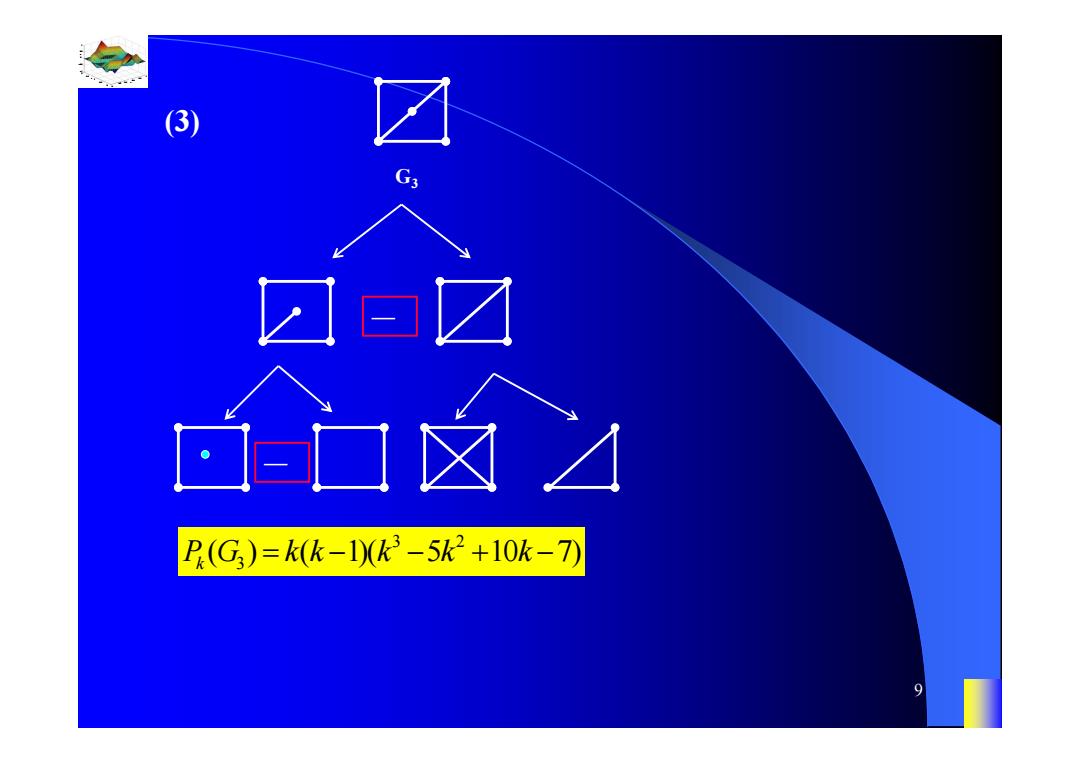
之 (3) G3 ☒ P.(G)=k(k-1k3-5k2+10k-7 9
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 (3) G3 — — 3 2 3 ( ) ( 1)( 5 10 7) PG kk k k k k

注:递推计数法的计算复杂度是指数型的。 2、理想子图计数法 (1)预备知识 定义1:设H是图G的生成子图。若H的每个分支均为 完全图,则称H是G的一个理想子图。用N,(G)表示G的 具有r个分支的理想子图的个数。 例2求N(G),N(G)。 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 注:递推计数法的计算复杂度是指数型的。 2、理想子图计数法 (1) 预备知识 定义1:设H是图G的生成子图。若H的每个分支均为 完全图,则称H是G的一个理想子图。用N r (G)表示G的 具有 r 个分支的理想子图的个数。 例2 求N4(G), N5(G)。 G
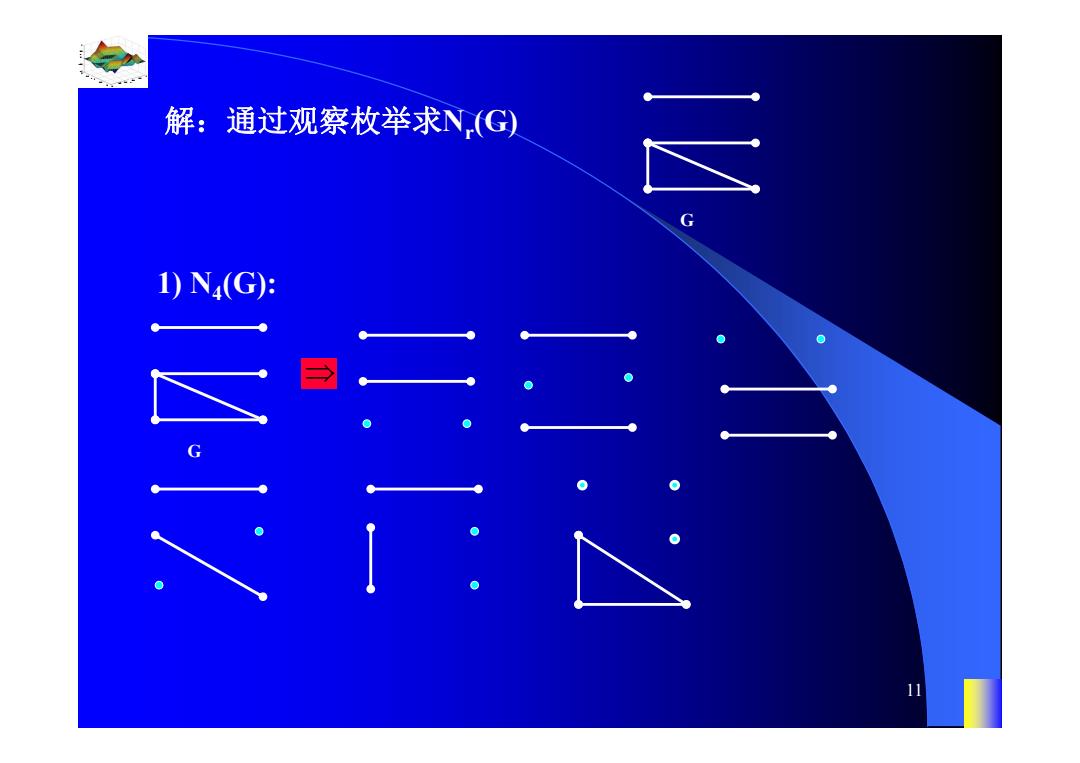
解:通过观察枚举求N(G) 三 1)N4(G): 11
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 解:通过观察枚举求Nr(G) G 1) N4(G): G