
第三章Sobolev空间 窦芳芳 December 15,2021 4口4+4左,4生+2分Q0 窝芳芳 第三幸Sobolev空间
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 第三章 Sobolev 空间 窦芳芳 December 15, 2021 窦芳芳 第三章 Sobolev 空间
Holder空间 经典Sobolev空间 3 Sobolev嵌入定理 基于L2的Sobolev空间 ●2=R”情形 。一般2情形 迹定理 时空Sobolev空间 4口4+4左,4生+主分QC 案芳芳 第三章Sobolev空间
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 Hölder 空间 2 经典 Sobolev 空间 3 Sobolev 嵌入定理 4 基于 L 2 的 Sobolev 空间 Ω = R n 情形 一般 Ω 情形 5 迹定理 6 时空 Sobolev 空间 窦芳芳 第三章 Sobolev 空间

Holder空间 设2CRn有界.定义Holder空间Cka(2)的目的是为了 “填平”连续可微函数C*(2)离散谱之间的“沟壑”.k十α可以被看 作是衡量C(R)函数所具有的正则性的:k阶导数,叠加一个额 外的a阶Holder连续性. C0,a(2)是C(2)的子空间,其范数定义为 IMc-m全mc网+,g二,feca ,ye2,x≠yX-ya 4口4+4左,4生+主分Q 实芳芳 第三幸Sobolev空
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Hölder 空间 设 Ω ⊂ R n 有界. 定义 Hölder 空间 C k,α(Ω) 的目的是为了 “填平”连续可微函数 C k (Ω) 离散谱之间的“沟壑”. k + α 可以被看 作是衡量 C k,α(R) 函数所具有的正则性的: k 阶导数, 叠加一个额 外的 α 阶 Hölder 连续性. C 0,α(Ω) 是 C 0 (Ω) 的子空间,其范数定义为 ||f||C0,α(Ω) △ = ||f||C0(Ω) + sup x,y∈Ω,x̸=y |f(x) − f(y)| |x − y| α , f ∈ C 0,α(Ω). 窦芳芳 第三章 Sobolev 空间

如果f有界且连续,则f∈C,a(2),近一步,对某些常数 C>0及所有X,y∈2满足Holder连续性界 lfx)-fy)川≤Cx-ye. 空间C,(2)容易看到仅仅是C(2)(有相同的范数).另外, C,1(2)是Lipschitz函数类,也被记为Lip(2)(C,1范数也被认 为是Lipschitz范数) 4口,4@,4左4生+主分QC 美芳芳 第三章Sobolev空间
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 如果 f 有界且连续,则 f ∈ C 0,α(Ω), 近一步,对某些常数 C > 0 及所有 x, y ∈ Ω 满足 Hölder 连续性界 |f(x) − f(y)| ≤ C|x − y| α . 空间 C 0,0 (Ω) 容易看到仅仅是 C 0 (Ω) (有相同的范数). 另外, C 0,1 (Ω) 是 Lipschitz 函数类, 也被记为 Lip(Ω) ( C 0,1 范数也被认 为是 Lipschitz 范数). 窦芳芳 第三章 Sobolev 空间

命题1.1 对每一0≤a≤1,C,a(2)为Banach空间. 命题1.2 对任意0≤a≤B≤1,C,a(2)C,8(①),且该嵌入连续. 命题1.3 如果a>1,则函数f的C,a(2)范数有限当且仅当f是常值的. 命题1.3解释了为什么一般情况下限制Hǒlder指标a小于 等于1. 4口,4+4左,4生+2分Q0 实芳芳 第三幸Sobolev空间
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 命题 1.1 对每一 0 ≤ α ≤ 1,C 0,α(Ω) 为 Banach 空间. 命题 1.2 对任意 0 ≤ α ≤ β ≤ 1,C 0,α(Ω) ⊃ C 0,β(Ω), 且该嵌入连续. 命题 1.3 如果 α > 1, 则函数 f 的 C 0,α(Ω) 范数有限当且仅当 f 是常值的. 命题 1.3 解释了为什么一般情况下限制 Hölder 指标 α 小于 等于 1. 窦芳芳 第三章 Sobolev 空间

对k∈NU{0},0≤a≤1,对f∈C(2),如果 Ilfil(兰∑Ia产flc.ag lal<k 为有限值,则称f∈C,a(2)CC(2) 命题1.4 Ck,a(2)是包含C+1(2)的Banach空间,且包含于C(2). 可构造出m阶连续微分算子L,连续映C+m,a(2)到 Ca(2). 设k,I∈NU{0},0≤a,B≤1.如果f∈Ca(), g∈C,B(2),k+a≤1+B,由定义知fg∈C@(2),且该乘法算子 从Ca(2)×C,B(2)到Cka(2)连续. 实芳芳 第三幸Sobolev空间
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 对 k ∈ N ∪ {0} , 0 ≤ α ≤ 1,对 f ∈ C k (Ω), 如果 ||f||Ck,α(Ω) △ = X |α|≤k ||∂ α f||C0,α(Ω) 为有限值,则称 f ∈ C k,α(Ω) ⊂ C k (Ω). 命题 1.4 C k,α(Ω) 是包含 C k+1(Ω) 的 Banach 空间,且包含于 C k (Ω). 可构造出 m 阶连续微分算子 L ,连续映 C k+m,α(Ω) 到 C k,α(Ω). 设 k, l ∈ N ∪ {0}, 0 ≤ α, β ≤ 1. 如果 f ∈ C k,α(Ω), g ∈ C l,β(Ω), k + α ≤ l + β, 由定义知 fg ∈ C k,α(Ω), 且该乘法算子 从 C k,α(Ω) × C l,β(Ω) 到 C k,α(Ω) 连续. 窦芳芳 第三章 Sobolev 空间
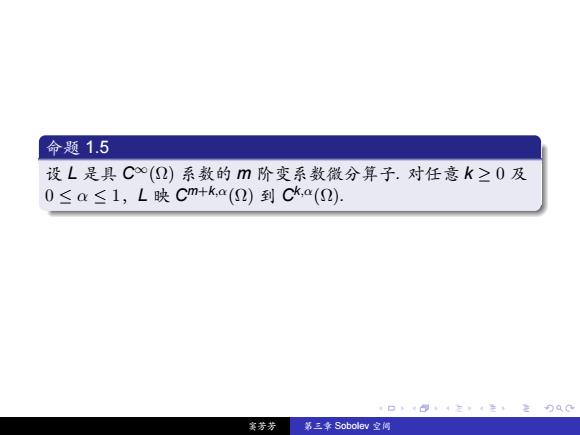
命题1.5 设L是具C(①)系数的m阶变系数微分算子.对任意k≥0及 0≤a≤1,L映Cm+k,a(2)到Ca(2) 4口4+4左,4生+2分Q0 实芳芳 第三幸Sobolev空间
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 命题 1.5 设 L 是具 C∞(Ω) 系数的 m 阶变系数微分算子. 对任意 k ≥ 0 及 0 ≤ α ≤ 1,L 映 C m+k,α(Ω) 到 C k,α(Ω). 窦芳芳 第三章 Sobolev 空间

设C0(2)是Ca(①)中紧支函数的闭包.该空间比Cka(2) 小 如,C(0,1)中的函数必定在端点{0,1}收敛于0,但 C0a(0,1)中的函数没有这一性质. 练习1.1 证明对任意k≥0及0≤a≤1,C8(R”)是C.0(R”)的稠子集 (Hint:用一个C函数通近C,a紧支函数,与一个逼近于恒等算 子光滑紧支函数卷积) 4口4+4左,4生+主分QC 实芳芳 第三幸Sobolev空
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 设 C k,α 0 (Ω) 是 C k,α(Ω) 中紧支函数的闭包. 该空间比 C k,α(Ω) 小. 如,C 0,α 0 ((0, 1)) 中的函数必定在端点 {0, 1} 收敛于 0, 但 C 0,α((0, 1)) 中的函数没有这一性质. 练习 1.1 证明对任意 k ≥ 0 及 0 ≤ α ≤ 1,C∞ c (R n ) 是 C k,α 0 (R n ) 的稠子集. (Hint: 用一个 C∞ c 函数逼近 C k,α 紧支函数, 与一个逼近于恒等算 子光滑紧支函数卷积.) 窦芳芳 第三章 Sobolev 空间

Holder空间在椭圆PDE中非常有用.下面给出一个典型例 子 设0<a<1,设f∈C0,a(R3)支集为B(0,1).设u是 Pos$ion方程-△u=f的唯一有界解,可表示为 u()dy. 4T JR3 lx-yl 则u∈C2,a(R3),且满足Schauder估计 llullc2.(3)<Callfllco.(3) 其中Ca仅依赖于a. 注1.1 Schauder估计当a=0时不成立. 这也是有必要引入Holder空间而不是更直观的C空间的原因。 实芳芳 第三幸Sobolev空
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Hölder 空间在椭圆 PDE 中非常有用. 下面给出一个典型例 子: 设 0 < α < 1, 设 f ∈ C 0,α(R 3 ) 支集为 B(0, 1). 设 u 是 Possion 方程 −∆u = f 的唯一有界解, 可表示为 u(x) △ = 1 4π Z R3 f(y) |x − y| dy. 则 u ∈ C 2,α(R 3 ), 且满足 Schauder 估计 ||u||C2,α(R3) ≤ Cα||f||C0,α(R3) 其中 Cα 仅依赖于 α. 注 1.1 Schauder 估计当 α = 0 时不成立. 这也是有必要引入 Hölder 空间而不是更直观的 C k 空间的原因。 窦芳芳 第三章 Sobolev 空间
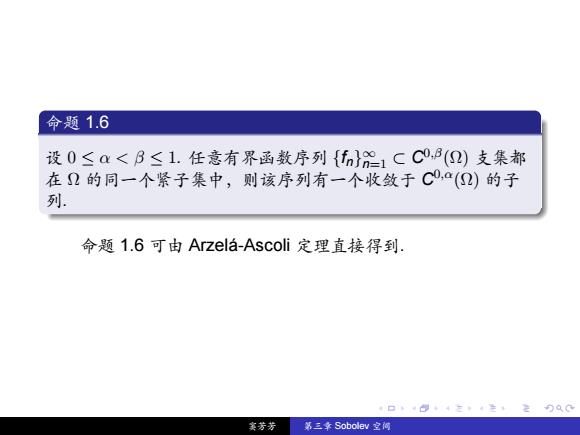
命题1.6 设0≤a<B≤1.任意有界函数序列{fn}e1CC,9()支集都 在2的同一个紧子集中,则该序列有一个收敛于C,(2)的子 列. 命题1.6可由Arzela-Ascoli定理直接得到 4口4+4左,4生+2分QC 实芳芳 第三幸Sobolev空间
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 命题 1.6 设 0 ≤ α < β ≤ 1. 任意有界函数序列 {fn}∞ n=1 ⊂ C 0,β(Ω) 支集都 在 Ω 的同一个紧子集中,则该序列有一个收敛于 C 0,α(Ω) 的子 列. 命题 1.6 可由 Arzelá-Ascoli 定理直接得到. 窦芳芳 第三章 Sobolev 空间