
第四章LP空间插值 窦芳芳 December 20,2021 日+021元克月00 实芳芳 第网章L”空间括值
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 第四章 L p 空间插值 窦芳芳 December 20, 2021 窦芳芳 第四章 L p 空间插值
①函数插值 ② 算子插值 ③插值例子 1口卡4回行4元电月风0 实芳芳 第网章L”空河精值
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 函数插值 2 算子插值 3 插值例子 窦芳芳 第四章 L p 空间插值
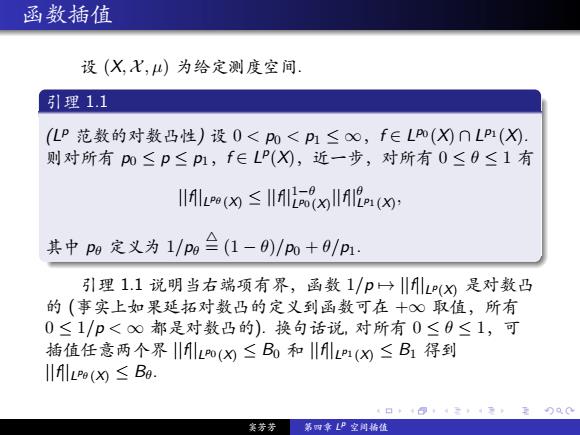
函数插值 设(X,X,)为给定测度空间. 引理1.1 (LP范数的对数凸性)设0<po<p1≤o∞,f∈L()∩LP(). 则对所有p0≤p≤p1,f∈LP(为,近一步,对所有0≤0≤1有 LP≤2(o: 其中pg定义为1/Pg≌(1-0)/p0+0/p1. 引理1.1说明当右端项有界,函数1/p→‖()是对数凸 的(事实上如果延拓对数凸的定义到函数可在十©取值,所有 0≤1/p<∞都是对数凸的).换句话说,对所有0≤0≤1,可 插值任意两个界‖Lo(X≤B和‖lL(≤B1得到 A LPO(≤Ba. 1日1回2,1无20a0 实芳芳 第网章L”空间精值
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 函数插值 设 (X, X , µ) 为给定测度空间. 引理 1.1 (Lp 范数的对数凸性) 设 0 < p0 < p1 ≤ ∞,f ∈ L p0 (X) ∩ L p1 (X). 则对所有 p0 ≤ p ≤ p1,f ∈ L p (X),近一步,对所有 0 ≤ θ ≤ 1 有 ||f||L pθ (X) ≤ ||f||1−θ L p0 (X) ||f||θ L p1 (X) , 其中 pθ 定义为 1/pθ △ = (1 − θ)/p0 + θ/p1. 引理 1.1 说明当右端项有界,函数 1/p 7→ ||f||Lp(X) 是对数凸 的 (事实上如果延拓对数凸的定义到函数可在 +∞ 取值,所有 0 ≤ 1/p < ∞ 都是对数凸的). 换句话说, 对所有 0 ≤ θ ≤ 1,可 插值任意两个界 ||f||L p0 (X) ≤ B0 和 ||f||L p1 (X) ≤ B1 得到 ||f||L pθ (X) ≤ Bθ. 窦芳芳 第四章 L p 空间插值

考虑强LP空间被替换成其弱组成LP,○.时的插值.给定可 测函数f:X→C,定义分布函数入f:R+→[0,十o]为 Mu(x∈X:li≥》=女e:d 由微积分等式有 由Fubini定理可得,对0<p<o Mw=pAee些 (1) 从而LP范数是广义函数的本质矩.L范数为 lllL∞(y=inf{t≥0:入(t)=0}: 口卡1回行元电月Q0 宾芳芳 第四章L”空川精值
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 考虑强 L p 空间被替换成其弱组成 L p,∞. 时的插值. 给定可 测函数 f : X → C, 定义分布函数 λf : R + → [0, +∞] 为 λf(t)µ({x ∈ X : |f(x)| ≥ t}) = ∫ X 1|f|≥t dµ. 由微积分等式有 |f(x)| p = p ∫ ∞ 0 1|f|≥t t p dt t . 由 Fubini 定理可得,对 0 < p < ∞ ||f||p Lp(X) = p ∫ ∞ 0 λf(t)t p dt t , (1) 从而 L p 范数是广义函数的本质矩. L∞ 范数为 ||f||L∞(X) = inf {t ≥ 0 : λf(t) = 0}. 窦芳芳 第四章 L p 空间插值

命题1.1 设f∈LP(.则存在两个常数cp和Cp使得如下关系式成立 cp∑M22p≤I1l-x≤Cp∑2)2, n∈Z nEZ 注1.1 命题1.1其建立了f的LP范数与分布函数的二元值入(2m)的关 系,即,对任意0<p≤∞,l?是与序列n→22)/P 的P(Z)范数可比的(取决于依赖于p的常数因子) 日+021元克月00 实芳芳 第网章L”空间括值
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 命题 1.1 设 f ∈ L p (X). 则存在两个常数 cp 和 Cp 使得如下关系式成立 cp ∑ n∈Z λf(2n )2np ≤ ||f||p Lp(X) ≤ Cp ∑ n∈Z λf(2n )2np . 注 1.1 命题 1.1 其建立了 f 的 L p 范数与分布函数的二元值 λf(2n ) 的关 系,即,对任意 0 < p ≤ ∞, ||f||Lp(X) 是与序列 n 7→ 2 nλf(2n ) 1/p 的 ℓ p (Z) 范数可比的 (取决于依赖于 p 的常数因子). 窦芳芳 第四章 L p 空间插值

近一步,由于对任意t>0, IMiw=人Pa≥/eP咖=PM0, 可得Chebyshev不等式 M田≤M呢w 00 记L,()为满足‖lL,∞(X<∞的可测函数f:X→C的弱范 数. 1口卡+01元电月只0 宾芳芳 第网章L”空河精值
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 近一步,由于对任意 t > 0, ||f||p Lp(X) = ∫ X |f| p dµ ≥ ∫ |f|≥t t p dµ = t pλf(t), 可得 Chebyshev 不等式 λf(t) ≤ 1 t p ||f||p Lp(X) . 0 0 tλf(t) 1/p . 记 L p,∞(X) 为满足 ||f||Lp,∞(X) < ∞ 的可测函数 f : X → C 的弱范 数. 窦芳芳 第四章 L p 空间插值

由Chebyshev不等式可得 llLP,∞(9≤lLP( 因此,LP(X)CLP,°(X).如果X=Rn具通常的Lebeague测度, 且0<p<∞,则函数fx三lXn/P是LP,∞(为的,但不在 LP(为中.因此,LP(X)LP,∞() 1日卡1回2元电月00 实芳芳 第网章L”空河精值
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 由 Chebyshev 不等式可得 ||f||Lp,∞(X) ≤ ||f||Lp(X) . 因此, L p (X) ⊂ L p,∞(X). 如果 X = R n 具通常的 Lebeague 测度, 且 0 < p < ∞, 则函数 f(x) △ = |x| −n/p 是 L p,∞(X) 的, 但不在 L p (X) 中. 因此,L p (X) ⫋ L p,∞(X). 窦芳芳 第四章 L p 空间插值

如果fg:X→C为两个函数,则有如下包含关系 {lf+gl≥t}cI1≥t/2}U{lg≥t/2} 因而 入f+g(t)≤入t/2)+入g(t/2): 可得拟三角不等式 lIf+gL,e(≤Cp(lflL,∞(y+llL,∞(N) 其中Cp是仅依赖于p的常数, 1日卡1回2元电月00 实芳芳 第网章L”空河精值
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 如果 f, g : X → C 为两个函数,则有如下包含关系 {|f + g| ≥ t} ⊂ {|f| ≥ t/2} ∪ {|g| ≥ t/2} 因而 λf+g(t) ≤ λf(t/2) + λg(t/2); 可得拟三角不等式 ||f + g||Lp,∞(X) ≤ Cp ( ||f||Lp,∞(X) + ||f||Lp,∞(X) ) 其中 Cp 是仅依赖于 p 的常数. 窦芳芳 第四章 L p 空间插值

命题1.2 设00, λ(t)≤ IAlR≈(凶 tPo 且 λt)≤ Al2为 tP1 从而,对所有0<0<1成立 入(t)≤ M2-3M tPo8+P1(1-例 口卡+回行1元电月00 实芳芳 第网章L”空间括值
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 命题 1.2 设 0 0, λf(t) ≤ ||f||p0 L p0,∞(X) t p0 且 λf(t) ≤ ||f||p1 L p1,∞(X) t p1 . 从而,对所有 0 < θ < 1 成立 λf(t) ≤ ||f||p0θ L p1,∞(X) ||f||p1(1−θ) L p1,∞(X) t p0θ+p1(1−θ) .✷ 窦芳芳 第四章 L p 空间插值

命题1.3 设0<P0<p≤o,f∈Lo()∩LP(.则对所有 0<p<p1有f∈LP(X),近一步,对所有0<0<1,有 lLP(为≤CmPm,llAl2*Xll1l-x (3) 其中指数P阳定义为1/P(1-)/p0+0/p. 证明.设to是使得 IAl8ox(凶 I8e(为 tPo tPi 成立的唯一t.将(9)中的0替换为0-e和0+e,其中 e∈0,0∩[0,1-.则有 λ(t)≤ IM2a-11 tPo(8-e)+p1(1-8+e) 口卡4回子1元电月00 实芳芳 第网章L”空间括值
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 命题 1.3 设 0 < p0 < p1 ≤ ∞,f ∈ L p0,∞(X) ∩ L p1,∞(X). 则对所有 p0 < p < p1 有 f ∈ L p (X), 近一步,对所有 0 < θ < 1, 有 ||f||L pθ (X) ≤ Cp0,p1,θ||f||θ L p0,∞(X) ||f||1−θ L p1,∞(X) , (3) 其中指数 pθ 定义为 1/pθ(1 − θ)/p0 + θ/p1. 证明. 设 t0 是使得 ||f||p0 L p0,∞(X) t p0 = ||f||p1 L p1,∞(X) t p1 成立的唯一 t. 将 (9) 中的 θ 替换为 θ − ε 和 θ + ε, 其中 ε ∈ [0, θ] ∩ [0, 1 − θ]. 则有 λf(t) ≤ ||f||p0(θ−ε) L p0,∞(X) ||f||p1(1−θ+ε) L p1,∞(X) t p0(θ−ε)+p1(1−θ+ε) 窦芳芳 第四章 L p 空间插值