记号 救敛性与连续性 Sobolev —辅助知识 窦芳芳 November 23, 2021 窦芳芳 Sobolev 辅助知识
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 记号 收敛性与连续性 Sobolev 空间 ——辅助知识 窦芳芳 November 23, 2021 窦芳芳 Sobolev 空间 ——辅助知识

记号 收敛社与连续州 记号 设F=R或C.对每个非负整n元数a=(a1,a2,,an), 记DP为阶数为ll=a1+a2十·+an的偏微分算子 alal 0x18x2.…0x始m 设区域2CR”.记 C()f:R:fis continuous } cm(2)≡{feC(2):DfeC(2)for all,la≤mh,m≥0, c(2)=∩cm(2) m>1 口卡4①21元克00 实芳芳 Sobolev空周 一满助知识
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 记号 收敛性与连续性 记号 设 F = R 或 C. 对每个非负整 n 元数 α = (α1, α2, . . . , αn) , 记 D α 为阶数为 |α| = α1 + α2 + · · · + αn 的偏微分算子 ∂ |α| ∂x α1 1 ∂x α2 2 · · · ∂x αn n . 设区域 Ω ⊂ R n . 记 C(Ω) △ = {f : Ω → R : f is continuous }, C m(Ω) △ = {f ∈ C(Ω) : D α f ∈ C(Ω) for all α, |α| ≤ m}, m ≥ 0, C ∞(Ω) = ∩ m≥1 C m(Ω). 窦芳芳 Sobolev 空间 ——辅助知识
记号 收敛性与连续州 记号 2中满足{x∈2:fx)≠0}的集合的闭包,记为supp(f) Co(2)是C()中有紧支集的函数的子集.类似地,定义 CW(2)=C"(2)∩Co(2).m≥1,C6(2)=C∞(2)nCo(2) 设21C2.记升2为函数f在21中的限制.令 cm(@)≌{a:f∈Cg(R)},C(@)e{An:feC6(R)} 口卡4回21元克000 实芳芳 Sobolev空博 一铺助知识
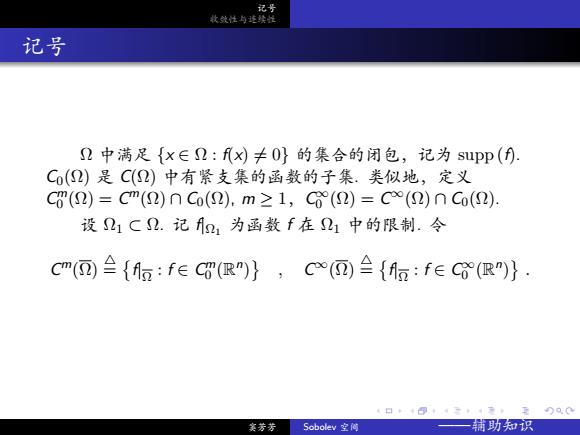
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 记号 收敛性与连续性 记号 Ω 中满足 {x ∈ Ω : f(x) 6= 0} 的集合的闭包,记为 supp (f). C0(Ω) 是 C(Ω) 中有紧支集的函数的子集. 类似地,定义 C m 0 (Ω) = C m(Ω) ∩ C0(Ω), m ≥ 1,C∞ 0 (Ω) = C∞(Ω) ∩ C0(Ω). 设 Ω1 ⊂ Ω. 记 f|Ω1 为函数 f 在 Ω1 中的限制. 令 C m(Ω) △ = { f|Ω : f ∈ C m 0 (R n ) } , C ∞(Ω) △ = { f|Ω : f ∈ C ∞ 0 (R n ) } . 窦芳芳 Sobolev 空间 ——辅助知识
记 收敛性与连续故 收敛性与连续性 定义 设V是一个线性空间.如果对于所有的a∈F,p(a)=|ap(V, p(M十吃)≤p(M)+p(№),v,M,2∈V,则泛函p:V→R称 为V上的半范.相应的,(V,p)称为半范空间. 1口卡4回子1元电月风0 实芳芳 Sobolev空博 一蒲助知识
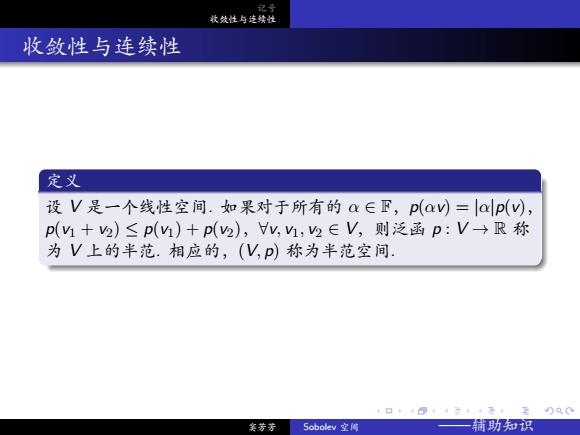
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 记号 收敛性与连续性 收敛性与连续性 定义 设 V 是一个线性空间. 如果对于所有的 α ∈ F,p(αv) = |α|p(v), p(v1 + v2) ≤ p(v1) + p(v2),∀v, v1, v2 ∈ V,则泛函 p : V → R 称 为 V 上的半范. 相应的,(V, p) 称为半范空间. 窦芳芳 Sobolev 空间 ——辅助知识

记男 收敛性与连续故 收敛性与连续性 引理 设(V,p)是一个半范空间,则 (1)lp()-p(2)I≤p(M-2),M,2∈V (2)p(M)≥0,M∈V, (3)核Ker(p)是V的一个子空间 (4)如果T∈C(W,),则poT:W→R是W上的一 个半范 (5)如果p是V上的一个半范且a≥0,1≤j≤n,则 aP是V上的一个半范。 如果p是对每个X卡0满足性质p(x)>0的半范,则其为 一个范数 实芳芳 Sobolev空g 满助知识
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 记号 收敛性与连续性 收敛性与连续性 引理 设 (V, p) 是一个半范空间,则 (1) |p(v1) − p(v2)| ≤ p(v1 − v2) , ∀ v1, v2 ∈ V, (2) p(v1) ≥ 0 , ∀ v1 ∈ V, (3) 核 Ker(p) 是 V 的一个子空间 (4) 如果 T ∈ L(W, V), 则 p ◦ T : W → R 是 W 上的一 个半范. (5) 如果 pj 是 V 上的一个半范且 αj ≥ 0, 1 ≤ j ≤ n, 则 ∑n j=1 αjpj 是 V 上的一个半范. 如果 p 是对每个 x 6= θ 满足性质 p(x) > 0 的半范,则其为 一个范数. 窦芳芳 Sobolev 空间 ——辅助知识

记 收敛性与连续故 收敛性与连续性 例 对每个KCC2,定义PK:C(2)→R为PK()=supxEKIf(x)I: 则PK是C(2)上的一个半范.另外,pn是C(①)上的一个范数. 对每个j,0≤j≤k,及KCC2通过 Pk()=sup{Def(x):x∈K,lal≤}可定义C*(2)上的一个半 范.每个这样的P?都是C*(①)上的一个范数. 1口10元11无克月00 实芳芳 Sobolev空傅 一满助知识
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 记号 收敛性与连续性 收敛性与连续性 例 对每个 K ⊂⊂ Ω, 定义 pK : C(Ω) → R 为 pK(f) = supx∈K |f(x)|. 则 pK 是 C(Ω) 上的一个半范. 另外,pΩ 是 C(Ω) ¯ 上的一个范数. 对每个 j, 0 ≤ j ≤ k, 及 K ⊂⊂ Ω 通过 pj,K(f) = sup{|D αf(x)| : x ∈ K, |α| ≤ j} 可定义 C k (Ω) 上的一个半 范. 每个这样的 pj,Ω 都是 C k (Ω) 上的一个范数. 窦芳芳 Sobolev 空间 ——辅助知识

记 收敛性与连续故 收敛性与连续性 定义 如果1imp(vk-)=0,则称V中序列{vk}1在v∈V中关 于p收敛 记为在(V,p)中Vn→V,当不致混淆时省略p 1口卡4回子1元电月风0 实芳芳 Sobolev空博 一满助知识
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 记号 收敛性与连续性 收敛性与连续性 定义 如果 lim k→∞ p(vk − v) = 0,则称 V 中序列 {vk} ∞ k=1 在 v ∈ V 中关 于 p 收敛. 记为在 (V, p) 中 vn → v,当不致混淆时省略 p. 设 S ⊂ V. S 的闭包在 (V, p) 中是集合 ¯S = {v ∈ V : 对某些S 中的序列{vn} ∞ n=1 , vn → v in (V, p)}. 如果 S = ¯S,S 称为闭的. S 的闭包 ¯S 是包含 {S : S ⊂ ¯S} 的 最小闭集, ¯S = ¯¯S, 如果 S ⊂ K = K¯ 则 ¯S ⊂ K. 窦芳芳 Sobolev 空间 ——辅助知识

记明 收敛性与连续战 收敛性与连续性 定义 如果1imp(vk-)=0,则称V中序列{vk}1在v∈V中关 于p收敛 记为在(V,p)中Vn→V,当不致混淆时省略p. 设SCV.S的闭包在(V,p)中是集合 5={v∈V:对某些S中的序列{n}e1n→vin(V,p) 4口卡4021元电月只0 实芳芳 Sobolev空博 一蒲助知识
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 记号 收敛性与连续性 收敛性与连续性 定义 如果 lim k→∞ p(vk − v) = 0,则称 V 中序列 {vk} ∞ k=1 在 v ∈ V 中关 于 p 收敛. 记为在 (V, p) 中 vn → v,当不致混淆时省略 p. 设 S ⊂ V. S 的闭包在 (V, p) 中是集合 ¯S = {v ∈ V : 对某些S 中的序列{vn} ∞ n=1, vn → v in (V, p)}. 如果 S = ¯S,S 称为闭的. S 的闭包 ¯S 是包含 {S : S ⊂ ¯S} 的 最小闭集, ¯S = ¯¯S, 如果 S ⊂ K = K¯ 则 ¯S ⊂ K. 窦芳芳 Sobolev 空间 ——辅助知识
记明 收敛性与连续故 收敛性与连续性 定义 如果1imp(vk-)=0,则称V中序列{vk}1在v∈V中关 于p收敛 记为在(V,p)中n→V,当不致混淆时省略P. 设SCV.S的闭包在(V,p)中是集合 5={v∈V:对某些S中的序列{vn}e1,n→vin(V,p)} 如果S=5,5称为闭的.S的闭包5是包含{5:5C5}的 最小闭集,5=5,如果SCK=衣则5CK 口卡4回于1元克月只0 实芳芳 Sobolev空博 一蒲助知识
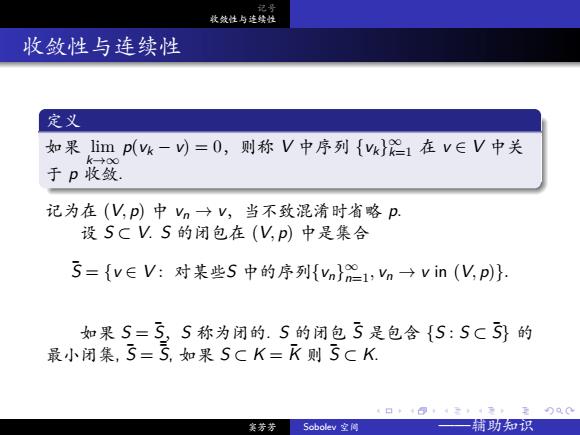
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 记号 收敛性与连续性 收敛性与连续性 定义 如果 lim k→∞ p(vk − v) = 0,则称 V 中序列 {vk} ∞ k=1 在 v ∈ V 中关 于 p 收敛. 记为在 (V, p) 中 vn → v,当不致混淆时省略 p. 设 S ⊂ V. S 的闭包在 (V, p) 中是集合 ¯S = {v ∈ V : 对某些S 中的序列{vn} ∞ n=1, vn → v in (V, p)}. 如果 S = ¯S,S 称为闭的. S 的闭包 ¯S 是包含 {S : S ⊂ ¯S} 的 最小闭集, ¯S = ¯¯S, 如果 S ⊂ K = K¯ 则 ¯S ⊂ K. 窦芳芳 Sobolev 空间 ——辅助知识
记 收敛性与连续故 收敛性与连续性 引理 设(V,p)是一个半范空间,M是V的一个子空间.则M是V的 一个子空间 1口卡4回行1元电月00 实芳芳 Sobolev空周 一满助知识
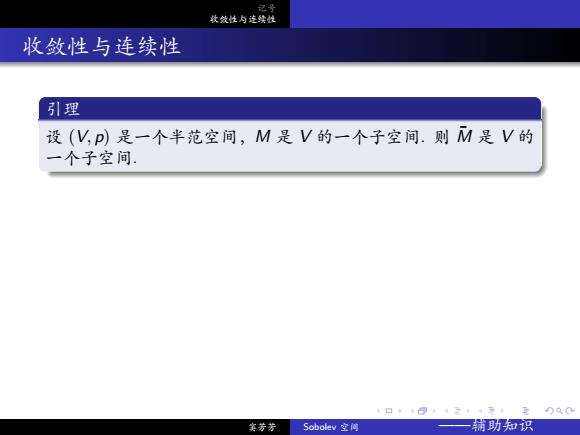
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 记号 收敛性与连续性 收敛性与连续性 引理 设 (V, p) 是一个半范空间,M 是 V 的一个子空间. 则 M¯ 是 V 的 一个子空间. 证明. 设 v1, v2 ∈ M¯ . 则存在 M 中的序列 {v1,k}∞ k=1 , {v2,k}∞ k=1,使得在 (V, p) 下,v1,k → v1,v2,k → v2 . 但 p((v1 + v2) − (v1,k + v2,k)) ≤ p(v1 − v1,k) + p(v2 − v2,k) → 0, 说明 (v1,k + v2,k) → v1 + v2 as n → ∞ 因为对 k ∈ N v1,k + v2,k ∈ M, 则 v1 + v2 ∈ M¯ . 类似地,对 α ∈ K 有 p(αv1 − αv1,k) = |α|p(v1 − v1,k) → 0, 从而 αv1 ∈ M¯ . 窦芳芳 Sobolev 空间 ——辅助知识