
本次课主要内容 有向图 (一)、有向图的概念与性质 (二)、有向图的连通性 (三)、图的定向问题
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (一)、有向图的概念与性质 (二)、有向图的连通性 有向图 (三)、图的定向问题

(一)、有向图的概念与性质 1、概念 定义1一个有向图D是指一个三元组VD),ED),中)。其 中,V(①)是非空的顶点集合,E(D)是不与V(D)相交的边集合, 而中D是关联函数,它使D的每条边对应D的有序顶点对不必 相异) 如果e是D的一条边,而u与v是使得中o(u,y=e的顶点, 那么称e是由u连接到v,记为e=。同时,称u为e的 弧尾(起点),v为e的弧头(终点)。 注:有向图可以简单地理解为“边有方向的图
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 1、概念 定义1 一个有向图D是指一个三元组(V(D) , E(D), фD)。其 中,V(D)是非空的顶点集合,E(D)是不与V(D)相交的边集合, 而фD是关联函数,它使D的每条边对应D的有序顶点对(不必 相异)。 如果e是D的一条边,而u与v是使得фD(u,v)=e的顶点, 那么称e是由u连接到v,记为e=。同时,称u为e的 弧尾(起点), v为e的弧头(终点)。 (一)、有向图的概念与性质 注:有向图可以简单地理解为“边有方向的图
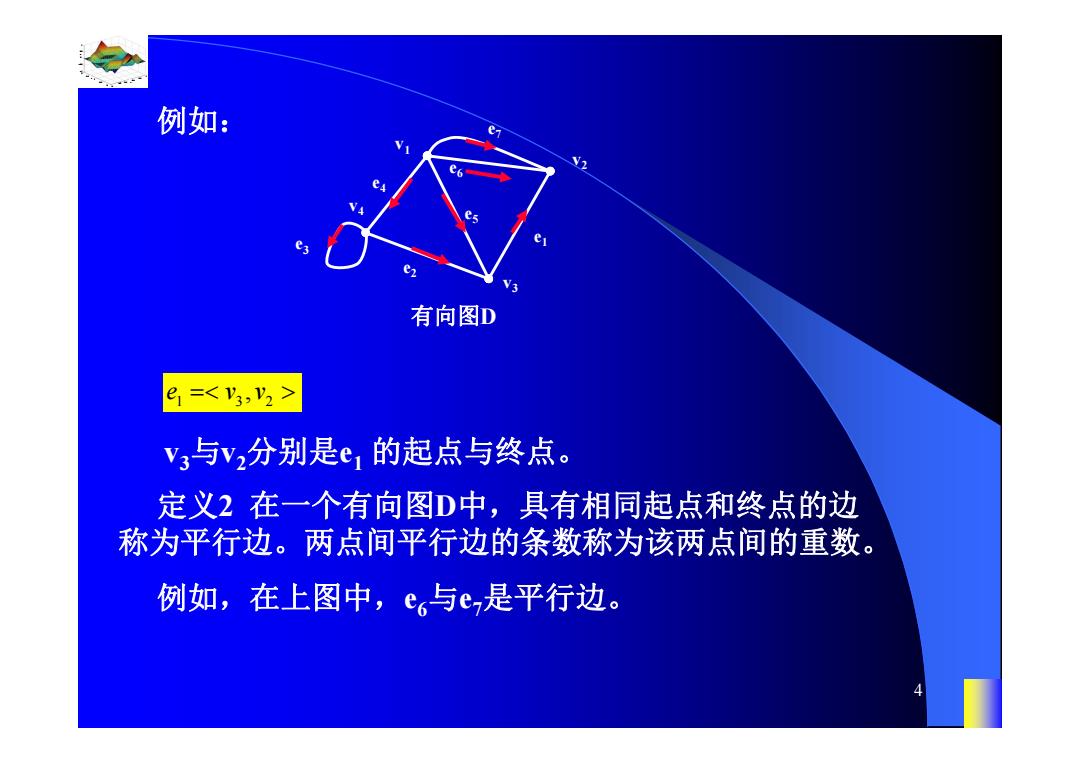
例如: e 有向图D e = v3与v分别是e,的起点与终点。 定义2在一个有向图D中,具有相同起点和终点的边 称为平行边。两点间平行边的条数称为该两点间的重数。 例如,在上图中,e。与e2是平行边
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 例如: 有向图D v4 v3 v2 v1 e2 e1 e4 e3 e6 e5 e7 1 32 e vv , v3与v2分别是e1 的起点与终点。 定义2 在一个有向图D中,具有相同起点和终点的边 称为平行边。两点间平行边的条数称为该两点间的重数。 例如,在上图中,e6与e7是平行边
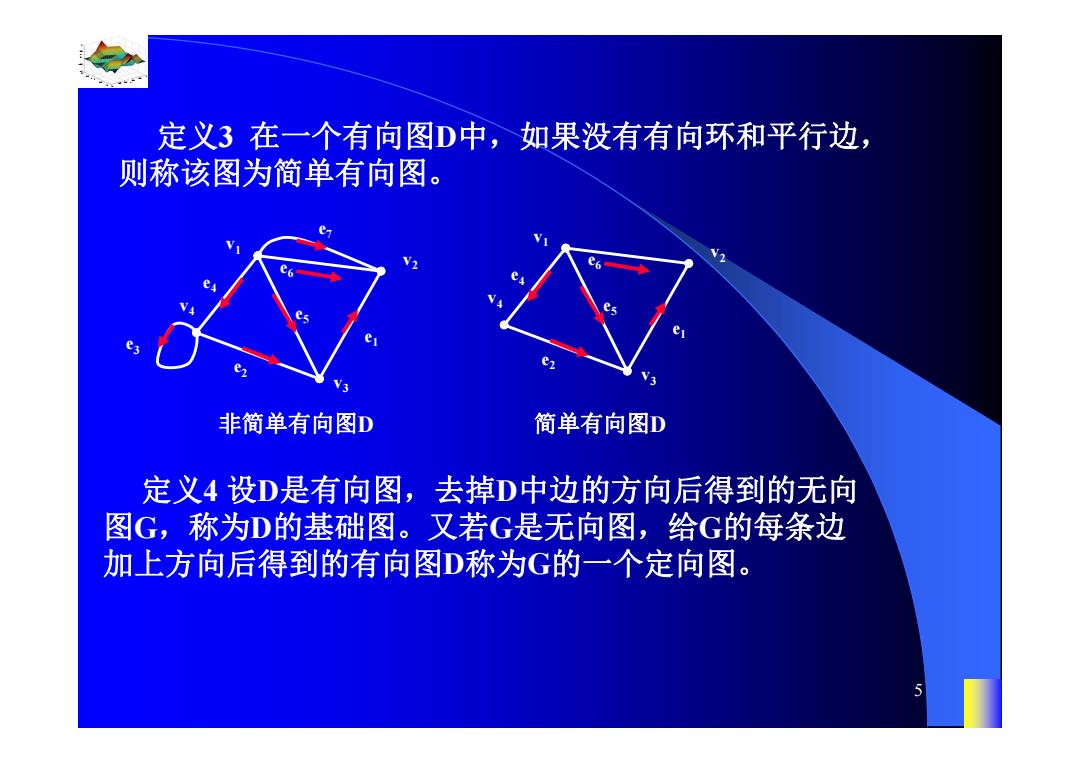
定义3在一个有向图D中,如果没有有向环和平行边, 则称该图为简单有向图。 非简单有向图D 简单有向图D 定义4设D是有向图,去掉D中边的方向后得到的无向 图G,称为D的基础图。又若G是无向图,给G的每条边 加上方向后得到的有向图D称为G的一个定向图
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 定义3 在一个有向图D中,如果没有有向环和平行边, 则称该图为简单有向图。 定义4 设D是有向图,去掉D中边的方向后得到的无向 图G,称为D的基础图。又若G是无向图,给G的每条边 加上方向后得到的有向图D称为G的一个定向图。 e3 非简单有向图D v4 v3 v2 v1 e2 e1 e4 e6 e5 e7 简单有向图D v4 v3 v2 v1 e2 e1 e4 e6 e5
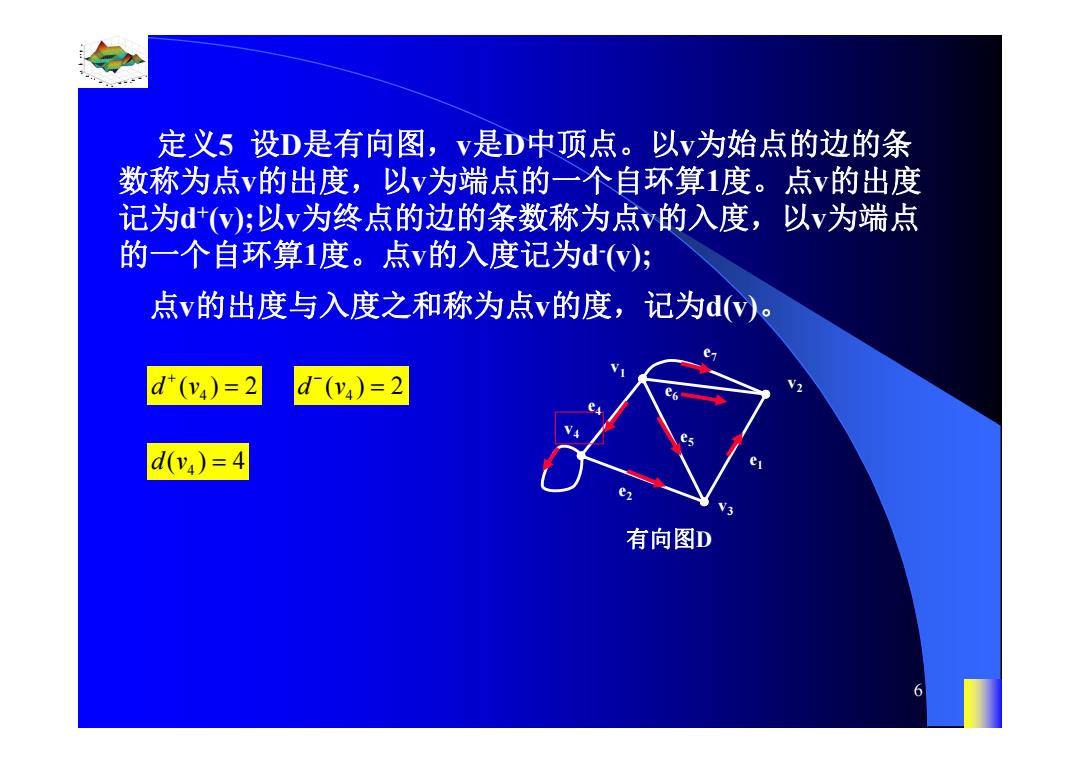
定义5设D是有向图,v是D中顶点。以v为始点的边的条 数称为点v的出度,以v为端点的一个自环算1度。点v的出度 记为d(w);以v为终点的边的条数称为点v的入度,以v为端点 的一个自环算1度。点v的入度记为d(w); 点v的出度与入度之和称为点v的度,记为d)。 d*(y4)=2 d(y4)=2 dv4)=4 有向图D 6
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 定义5 设D是有向图,v是D中顶点。以v为始点的边的条 数称为点v的出度,以v为端点的一个自环算1度。点v的出度 记为d+(v);以v为终点的边的条数称为点v的入度,以v为端点 的一个自环算1度。点v的入度记为d-(v); 点v的出度与入度之和称为点v的度,记为d(v)。 有向图D v4 v3 v2 v1 e2 e1 e4 e6 e5 e7 4 d v() 2 4 d v() 2 4 d v() 4

例1一个简单图有多少个定向图? 答:因为每条边有2种定向方式,所以共有2mG种定向。 例2求证:G存在一个定向图D,使得对v∈V(D),有 d()-d(s1 证明:不失一般性,设G是连通图。G中奇度顶点个数必 然为偶数个,将偶数个奇数度顶点配对,然后在每一对配对 顶点间连一条边得到欧拉图G1。在G,中用Fluery:算法求出G 的一欧拉环游C,然后顺次地在C上标上方向,由此得到C的 定向图C 在C,中,去掉添加的边后,得到G的定向图D.显然:
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 例1 一个简单图有多少个定向图? 答:因为每条边有2种定向方式,所以共有2 m(G)种定向。 例2 求证:G存在一个定向图D,使得对 ,有 v VD( ) dv dv () () 1 证明:不失一般性,设G是连通图。G中奇度顶点个数必 然为偶数个,将偶数个奇数度顶点配对,然后在每一对配对 顶点间连一条边得到欧拉图G1。在G1中用Fluery算法求出G 的一欧拉环游C,然后顺次地在C上标上方向,由此得到C的 定向图C1。 在C1中,去掉添加的边后,得到G的定向图D.显然:

对vEV(D),有 d"(v)-d()s1 2、性质 定理1设D=(V,E)是有向图,则: ∑d(y)=∑d(m)=m(D) vEV(D) vEV(D) 证明:由出度与入度的定义立即可得上面等式。 3、有向图的矩阵表示 8
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 对 ,有 v VD( ) dv dv () () 1 2、性质 定理1 设D=(V, E)是有向图,则: () () () () ( ) vVD vVD d v d v mD 证明:由出度与入度的定义立即可得上面等式。 3、有向图的矩阵表示

定义6设D=(V,E)是有向图,其中V={v1V2,Vm} E=fepe2....em} ()称AD=(a)nxm是D的邻接矩阵,其中a是v为始点, v为终点的边的条数,1i≤n,1j≤n。 (2)若D无环。称矩阵M=(mm×m是D的关联矩阵,其中 1,y,是e的始点, -l,y,是边e的终点,(1≤i≤n,l≤j≤m), 0,其它
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 E={e1,e2,…,em} (1) 称A(D)=(aij) n×n是D的邻接矩阵,其中aij是vi为始点, vj为终点的边的条数,1≦i≦n,1≦j≦n。 定义6 设D=(V,E)是有向图,其中V={v1,v2,…,vn} (2) 若D无环。称矩阵M=(mij)n×m是D的关联矩阵,其中 1, -1 (1 ,1 ), 0, . i j ij i j v e m v e in j m 是 的始点, , 是边 的终点, 其它
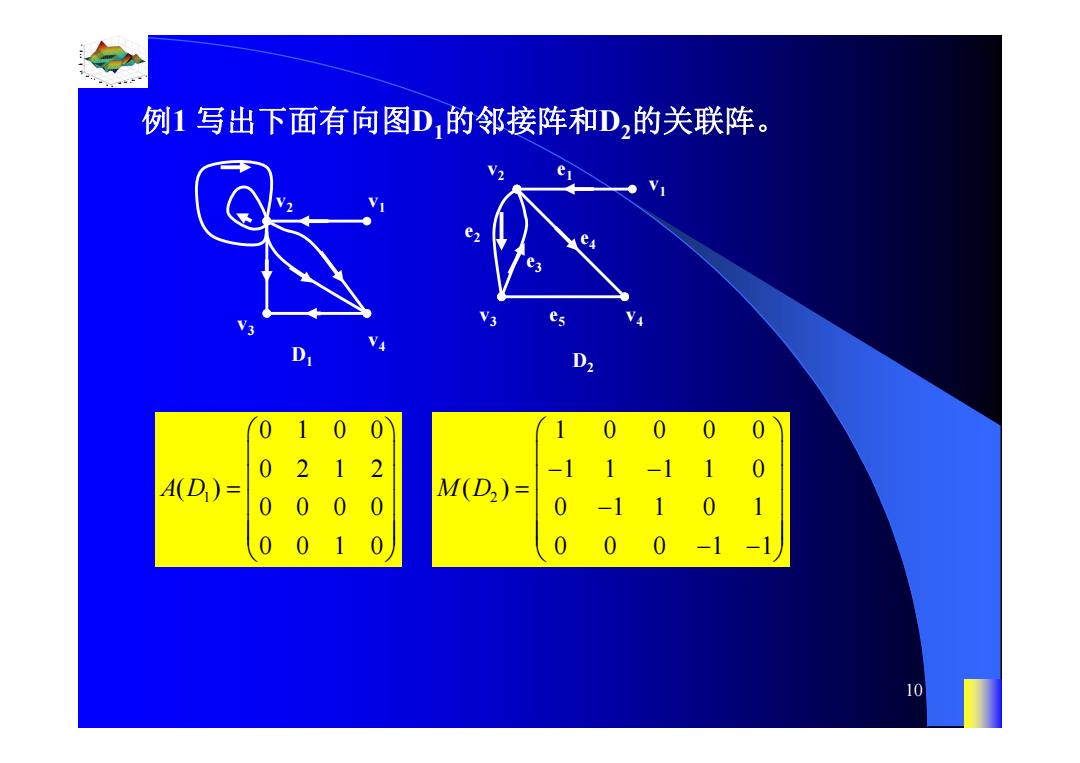
例1写出下面有向图D,的邻接阵和D,的关联阵。 es D 0 0 0 A(D)= M(D2)= 0 0 0 0 0 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 例1 写出下面有向图D1的邻接阵和D2的关联阵。 v4 v3 v2 v1 D1 v3 v4 v2 v1 e1 e4 e3 e2 e5 D2 1 0100 0212 ( ) 0000 0010 A D 2 10000 11 11 0 ( ) 0 11 0 1 000 11 M D

(二)、有向图的连通性 1、相关概念 (1)有向途径(闭途径)、迹(闭迹)和路(圈) 上面概念与无向图中相关概念类似。 (2)有向图中顶点间的连通性 定义7设D=(V,E)是有向图,u与v是D中两个顶点。 1)若D中存在一条(u,v)路,则称u可达y,记为u→V。 规定u→u。 2)若D中存在一条(u,v)路或,u)路,则称u与v是单 向连通的
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 1、相关概念 (二)、有向图的连通性 (1) 有向途径(闭途径)、迹(闭迹)和路(圈) 上面概念与无向图中相关概念类似。 (2) 有向图中顶点间的连通性 定义7 设D=(V, E)是有向图,u与v是D中两个顶点。 1) 若D中存在一条(u,v)路,则称u可达v,记为u→v。 规定u →u。 2) 若D中存在一条(u,v)路或(v, u)路,则称u与v是单 向连通的