
本次课主要内容 超哈密尔顿图与超可迹图问题 (一)、超H图与超可迹图 (二)、E图和H图的关系
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (二)、E图和H图的关系 超哈密尔顿图与超可迹图问题 (一)、超H图与超可迹图

(一)、超H图与超H迹 定义1若图G是非H图,但对于G中任意点v,都有G-v是 H图,则称G是超H图。 定理1彼得森图是超H图。 彼得森图 证明:(1)证明彼得森图是非H图
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 定义1 若图G是非H图,但对于G中任意点v,都有G-v是 H图,则称G是超H图。 (一)、超H图与超H迹 定理1 彼得森图是超H图。 1 7 6 5 4 2 3 彼得森图 10 9 8 证明: (1) 证明彼得森图是非H图

若不然,设C是G的H圈。 对于边12,17,15来说,必然有两条边在C中。不失一般性, 假定17,12在C中,那么,56,54也必然在C中。 彼得森图 又对于边28,23来说,在前面情况下,必有一条在C中 分两种情形讨论
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 若不然,设C是G的H圈。 1 6 5 4 2 3 7 彼得森图 10 9 8 又对于边28,23来说,在前面情况下,必有一条在C中。 分两种情形讨论。 对于边12, 17,15来说,必然有两条边在C中。不失一般性, 假定17,12在C中,那么,56,54也必然在C中
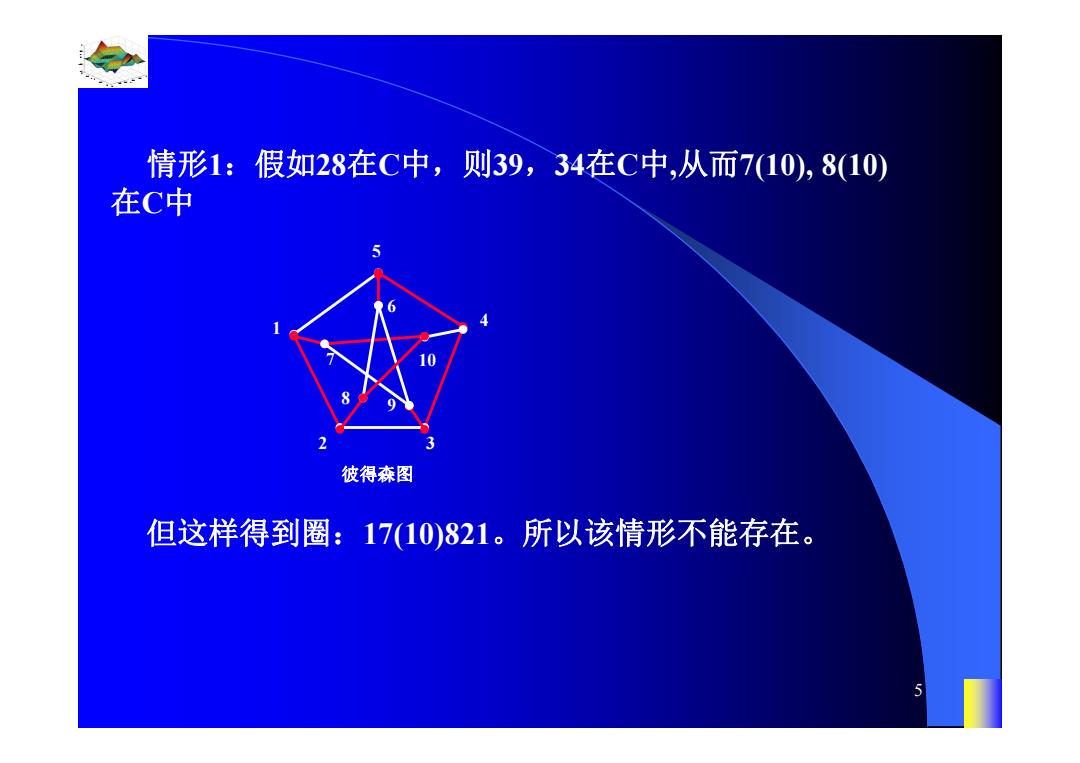
情形1:假如28在C中,则39,34在C中,从而710),8(10) 在C中 彼得森图 但这样得到圈:17(10)821。所以该情形不能存在
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 1 6 5 4 2 3 7 彼得森图 10 9 8 但这样得到圈:17(10)821。所以该情形不能存在。 情形1:假如28在C中,则39,34在C中,从而7(10), 8(10) 在C中
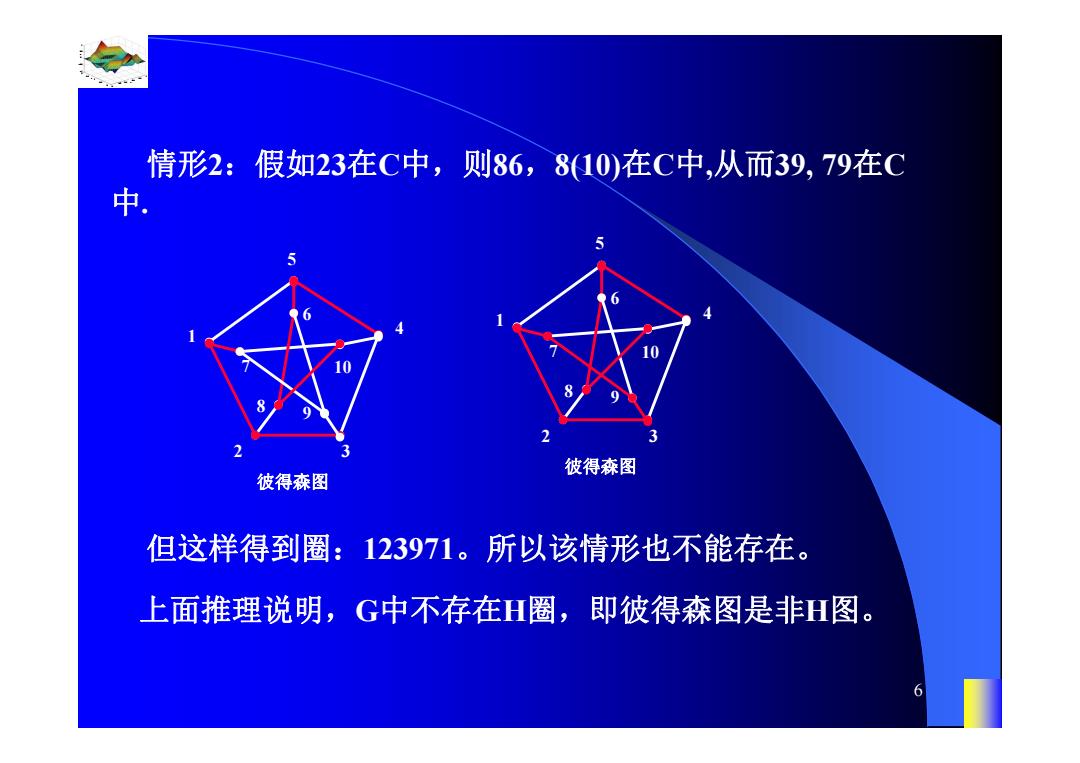
情形2:假如23在C中,则86,810)在C中,从而39,79在C 中. 彼得森图 彼得森图 但这样得到圈:123971。所以该情形也不能存在。 上面推理说明,G中不存在H圈,即彼得森图是非H图。 6
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 但这样得到圈:123971。所以该情形也不能存在。 情形2:假如23在C中,则86,8(10)在C中,从而39, 79在C 中. 1 6 5 4 2 3 7 彼得森图 10 9 8 1 6 5 4 2 3 7 彼得森图 10 9 8 上面推理说明,G中不存在H圈,即彼得森图是非H图
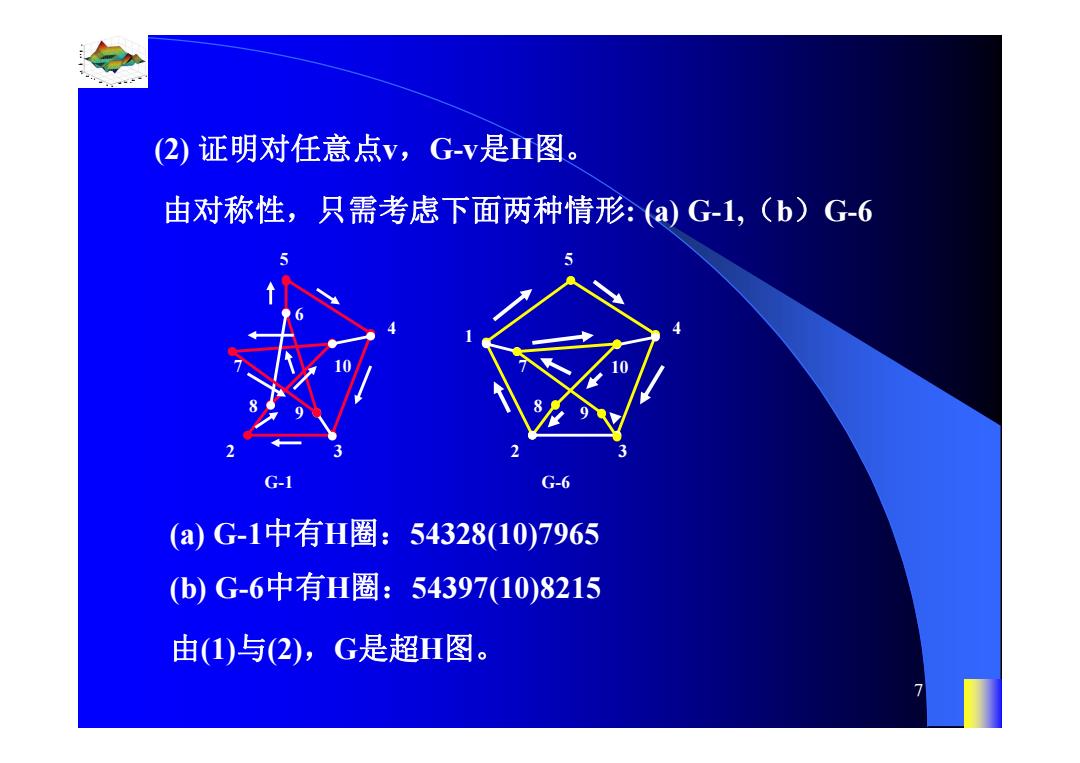
(2)证明对任意点v,G-v是H图.。 由对称性,只需考虑下面两种情形:(a)G-1,(b)G-6 G-1 G-6 (a)G-1中有H圈:54328(10)7965 (b)G-6中有H圈:54397(10)8215 由(1)与(2),G是超H图
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 由对称性,只需考虑下面两种情形: (a) G-1,(b)G-6 (2) 证明对任意点v,G-v是H图。 (a) G-1中有H圈:54328(10)7965 3 6 5 4 2 7 10 G-1 9 8 (b) G-6中有H圈:54397(10)8215 1 5 4 2 3 7 G-6 10 9 8 由(1)与(2),G是超H图

定义2若G中没有H路,但是对G中任意点v,G-v存在 H路,则称G是超可迹的。 数学家加莱曾经猜想:不存在超可迹的图。但该猜想被 Horton和Thomassen以构图的方式否定了。 定理2 Thomassen图是超可迹图。 Thomassen图 8
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 定义2 若G中没有H路,但是对G中任意点v,G-v存在 H路,则称G是超可迹的。 数学家加莱曾经猜想:不存在超可迹的图。但该猜想被 Horton和Thomassen以构图的方式否定了。 定理2 Thomassen图是超可迹图。 b a e d f c Thomassen图 Ⅰ Ⅱ Ⅲ Ⅳ

定理证明分为两部分:(1)证明G中不存在H路;(2)证 明对G中任意点v,有G-v存在H路。 (1)证明G中不存在H路。 如图所示,将G用虚线分成对称 中年。中年年。9中年9 的4部分:I,Ⅱ,Ⅲ,V。 假设G有H路P,设该路的起点为a, 终点为B。 不失一般性,设a∈IU(a}。 Thomassen图 断言1:IU{a}中不存在以a,c,d三点中任意两点为 端点的H路。 若不然,将推出彼得森图是H图
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 定理证明分为两部分: (1) 证明G中不存在H路;(2) 证 明对G中任意点v,有G-v存在H路。 (1) 证明G中不存在H路。 如图所示,将G用虚线分成对称 的4部分:Ⅰ,Ⅱ,Ⅲ,Ⅳ 。 b a e d f c Thomassen图 Ⅰ Ⅱ Ⅲ Ⅳ 假设G有H路P,设该路的起点为α, 终点为β。 不失一般性,设α∈ Ⅰ∪{a}。 断言1: Ⅰ∪{a} 中不存在以a , c , d三点中任意两点为 端点的H路。 若不然,将推出彼得森图是H图
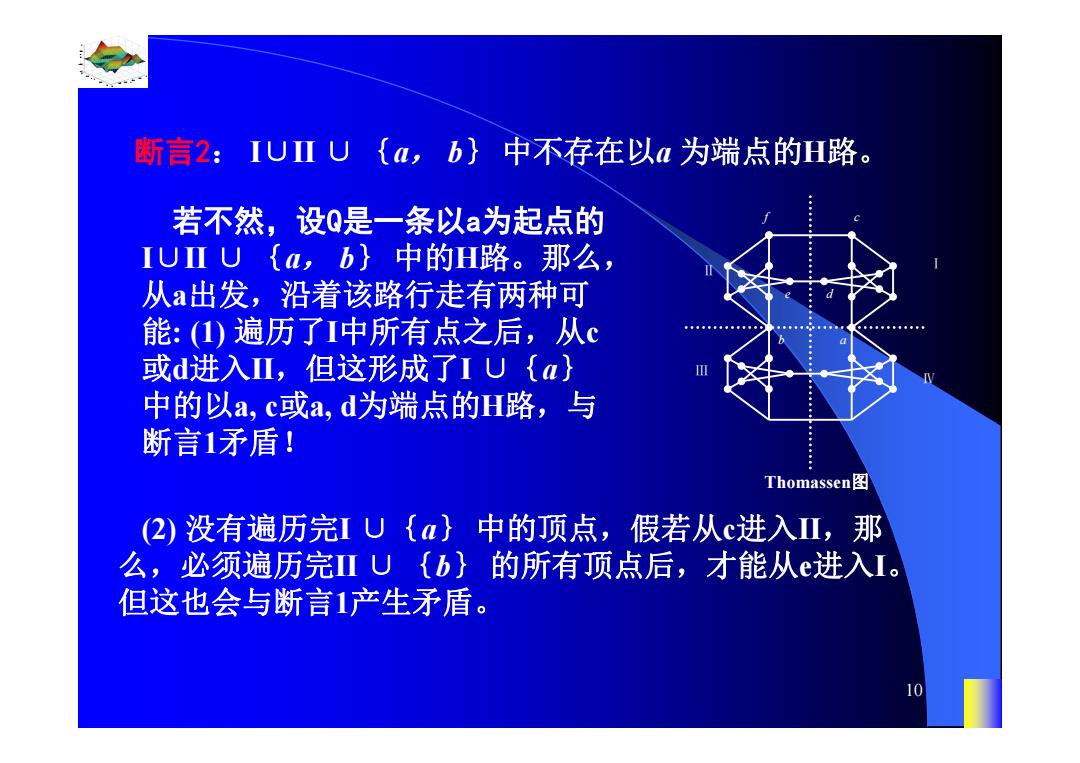
断言2:IUⅡU {a,b}中不存在以a为端点的H路 若不然,设Q是一条以a为起点的 IUⅡU{a,b}中的H路。那么, 从a出发,沿着该路行走有两种可 能:(1)遍历了I中所有点之后,从c 或d进入Ⅱ,但这形成了1U{a} 中的以a,c或a,d为端点的H路,与 断言1矛盾! Thomassen图 (2)没有遍历完IU{a中的顶点,假若从c进入Ⅱ,那 么,必须遍历完ⅡU{b}的所有顶点后,才能从e进入I。 但这也会与断言1产生矛盾。 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 b a e d f c Thomassen图 Ⅰ Ⅱ Ⅲ Ⅳ 断言2: Ⅰ∪Ⅱ ∪ {a, b} 中不存在以a 为端点的H路。 若不然,设Q是一条以a为起点的 Ⅰ∪Ⅱ ∪ {a, b} 中的H路。那么, 从a出发,沿着该路行走有两种可 能: (1) 遍历了Ⅰ中所有点之后,从c 或d进入Ⅱ,但这形成了Ⅰ ∪{a} 中的以a, c或a, d为端点的H路,与 断言1矛盾! (2) 没有遍历完Ⅰ ∪{a} 中的顶点,假若从c进入Ⅱ,那 么,必须遍历完Ⅱ ∪ {b} 的所有顶点后,才能从e进入Ⅰ。 但这也会与断言1产生矛盾

由前面假设:a∈IU{a}。 情形1:a=a 我们沿着P作如下的行进: (1)假设是由a进入I,要能够走完P, 必须遍历IUⅡ的所有顶点后由b进 入皿,但这与断言2矛盾! (2)假设是由a进入V,要能够走 完P,必须遍历ⅢUV的所有顶点后 Thomassen图 由b进入Ⅱ,但这也与断言2矛盾! 所以,情形1不能成立!
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 b a e d f c Thomassen图 Ⅰ Ⅱ Ⅲ Ⅳ 情形1:α= a 所以,情形1不能成立! 由前面假设:α∈ Ⅰ∪{a}。 我们沿着P作如下的行进: (1) 假设是由a进入Ⅰ,要能够走完P, 必须遍历Ⅰ∪Ⅱ 的所有顶点后由b进 入Ⅲ,但这与断言2矛盾! (2) 假设是由a进入Ⅳ,要能够走 完P,必须遍历Ⅲ∪Ⅳ 的所有顶点后 由b进入Ⅱ,但这也与断言2矛盾!