
Advanced Algorithms LP Duality 尹一通Nanjing University,2022Fall
尹⼀通 Nanjing University, 2022 Fall Advanced Algorithms LP Duality
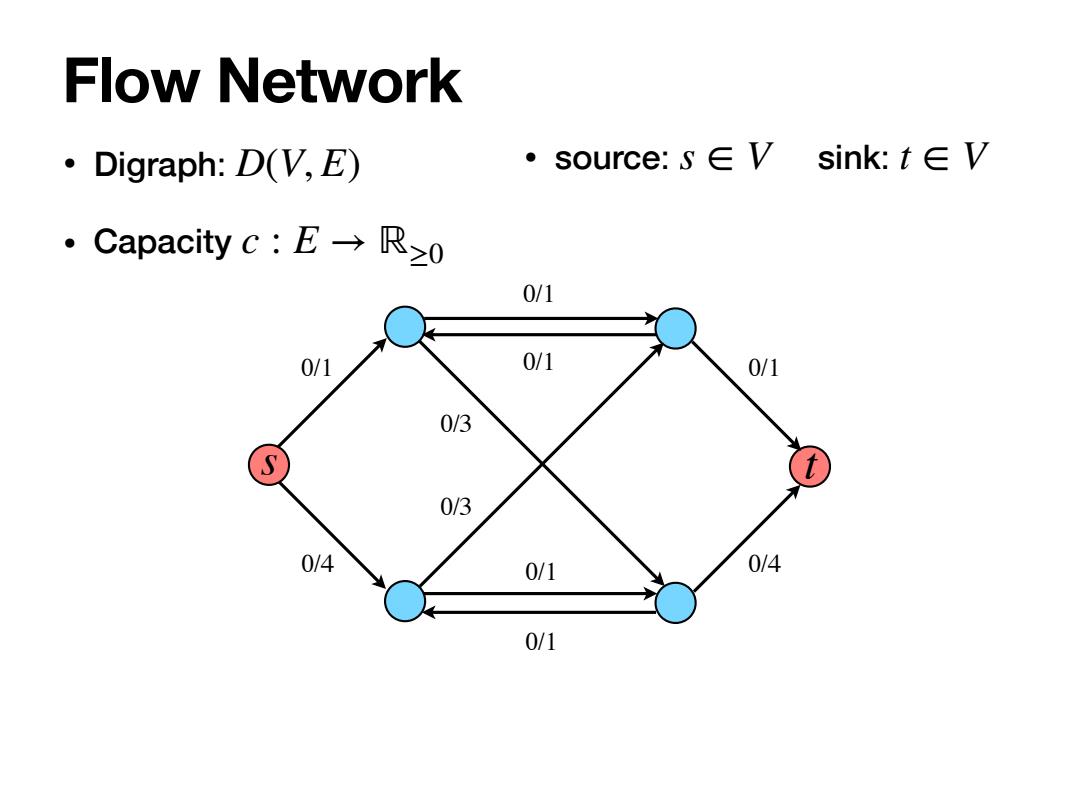
Flow Network ·Digraph:D(V,E) source:S∈V sink:t∈V .Capacity c:E→R≥o 0/1 0/1 0/1 0/1 0/3 S 0/3 0/4 0/1 0/4 0/1
• Digraph: • Capacity D(V, E) c : E → ℝ≥0 Flow Network 0/1 0/4 0/1 0/1 0/1 0/1 0/1 0/4 0/3 0/3 s t • source: sink: • Flow s ∈ V t ∈ V f : E → ℝ≥0
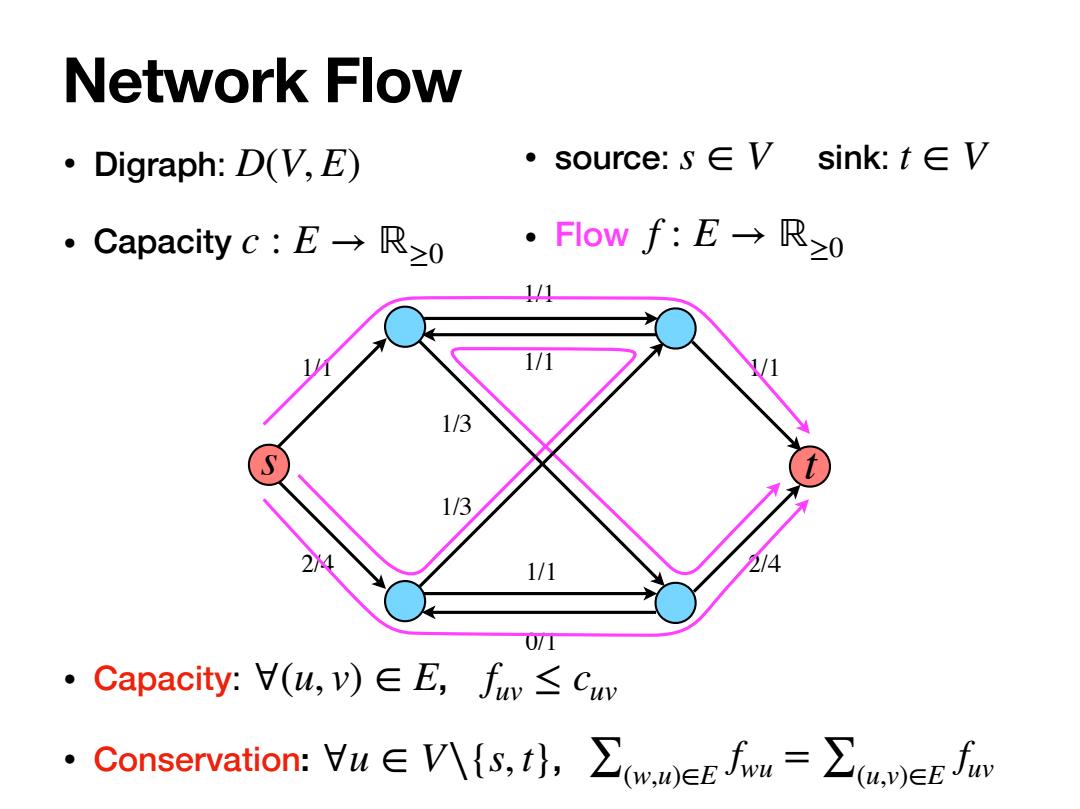
Network Flow ·Digraph:D(V,E) ·source:s∈V sink:t∈V 。Capacity c:E→Ro ·F1owf:E→R≥0 11 1/3 1/3 1/1 214 0/1 ·Capacity:H(u,)∈E,fw≤Cuw ·Conservation::Vu∈八{s,t,∑wEEw=∑u,beE Jin
• Digraph: • Capacity D(V, E) c : E → ℝ≥0 Network Flow • source: sink: • Flow s ∈ V t ∈ V f : E → ℝ≥0 • Capacity: , • Conservation: , ∀(u, v) ∈ E f uv ≤ cuv ∀u ∈ V∖{s, t} 1/1 2/4 0/1 1/1 1/1 1/1 1/1 2/4 1/3 1/3 ∑(w,u)∈E f wu = ∑(u,v)∈E f uv s t
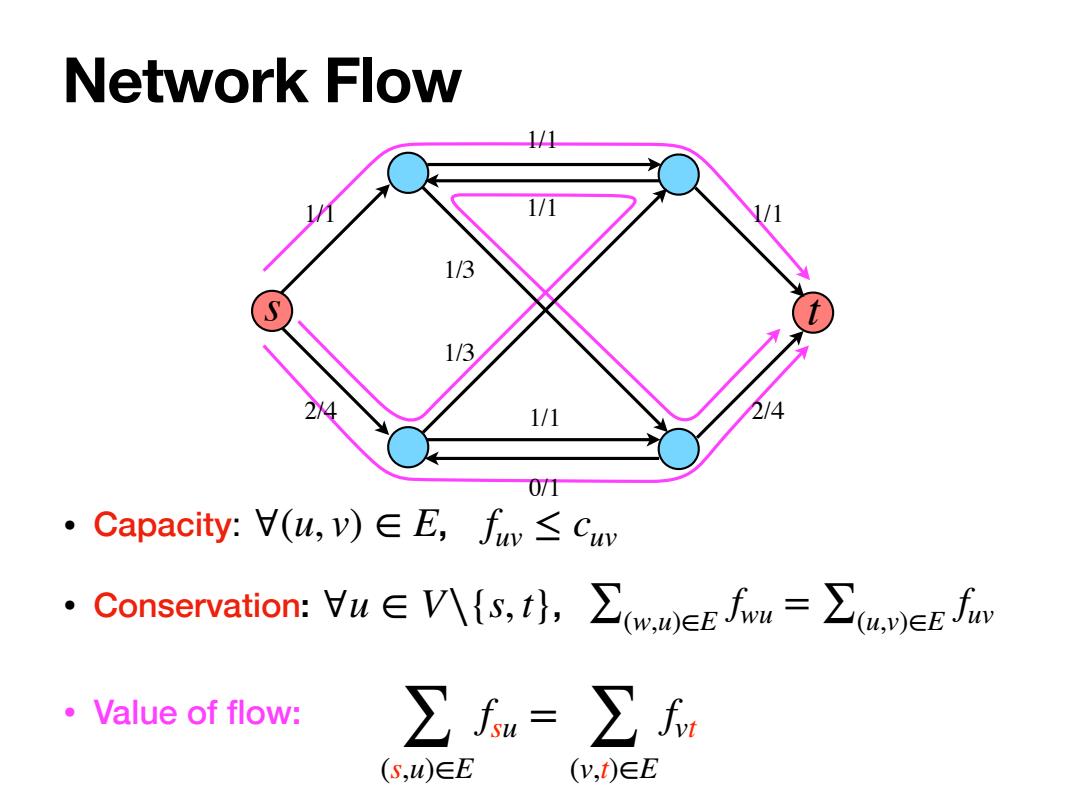
Network Flow 1/4 1/3 1/3 1/1 2/4 071 ·Capacity::(u,v)∈E,fw≤Cuv ·Conservation:Vu∈V\{s,th,∑DE=∑uyeE fiw 。Value of flow: ∑fu=∑r (S,u)∈E (v,t)∈E
Network Flow • Capacity: , • Conservation: , ∀(u, v) ∈ E f uv ≤ cuv ∀u ∈ V∖{s, t} ∑(w,u)∈E f wu = ∑(u,v)∈E f uv ∑ (s,u)∈E f su = ∑ (v,t)∈E f vt • Value of flow: 1/1 2/4 0/1 1/1 1/1 1/1 1/1 2/4 1/3 1/3 s t
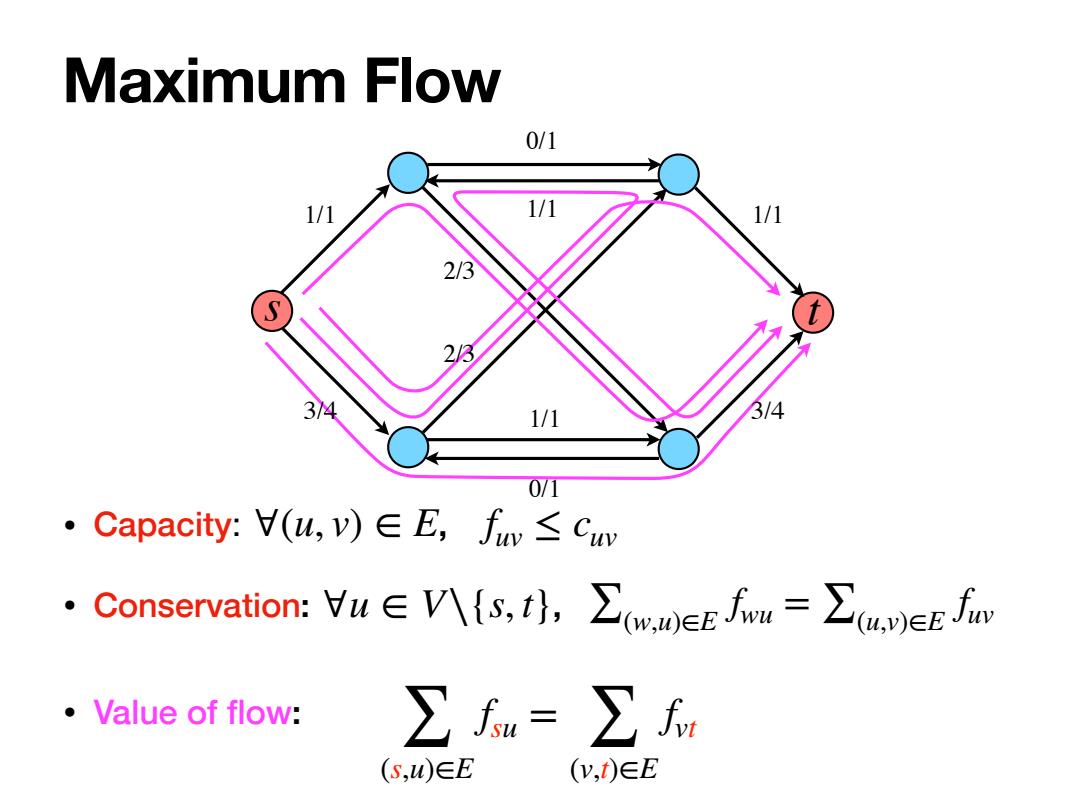
Maximum Flow 0/1 1/1 1/1 1/1 2/3 S 23 34 1/1 3/4 0/1 ·Capacity:(u,v)∈E,fw≤Cuw ·Conservation:Vu∈V八{s,t,∑wEF Fiv=∑u,ner fio ·Value of flow: ∑fu=∑r (S,u)∈E (v,t)∈E
Maximum Flow • Capacity: , • Conservation: , ∀(u, v) ∈ E f uv ≤ cuv ∀u ∈ V∖{s, t} ∑(w,u)∈E f wu = ∑(u,v)∈E f uv ∑ (s,u)∈E f su = ∑ (v,t)∈E f vt • Value of flow: s t 1/1 3/4 0/1 1/1 1/1 0/1 1/1 3/4 2/3 2/3

Cut ·Digraph:D(V,E) ·source:s∈V sink:t∈V ·Capacity c:E→R0·Cut ScV,s∈S,ttS 0/1 0/1 0/1 0/1 0/3 0/3 0/4 ,0/1 0/1 。Value of cut: Σ Cuv u∈S,v庄S,(u,v)∈E
• Digraph: • Capacity D(V, E) c : E → ℝ≥0 Cut 0/1 0/4 0/1 0/1 0/1 0/1 0/1 0/4 0/3 0/3 s t • source: sink: • Cut , , s ∈ V t ∈ V S ⊂ V s ∈ S t ∉ S • Value of cut: ∑ u∈S,v∉S,(u,v)∈E cuv
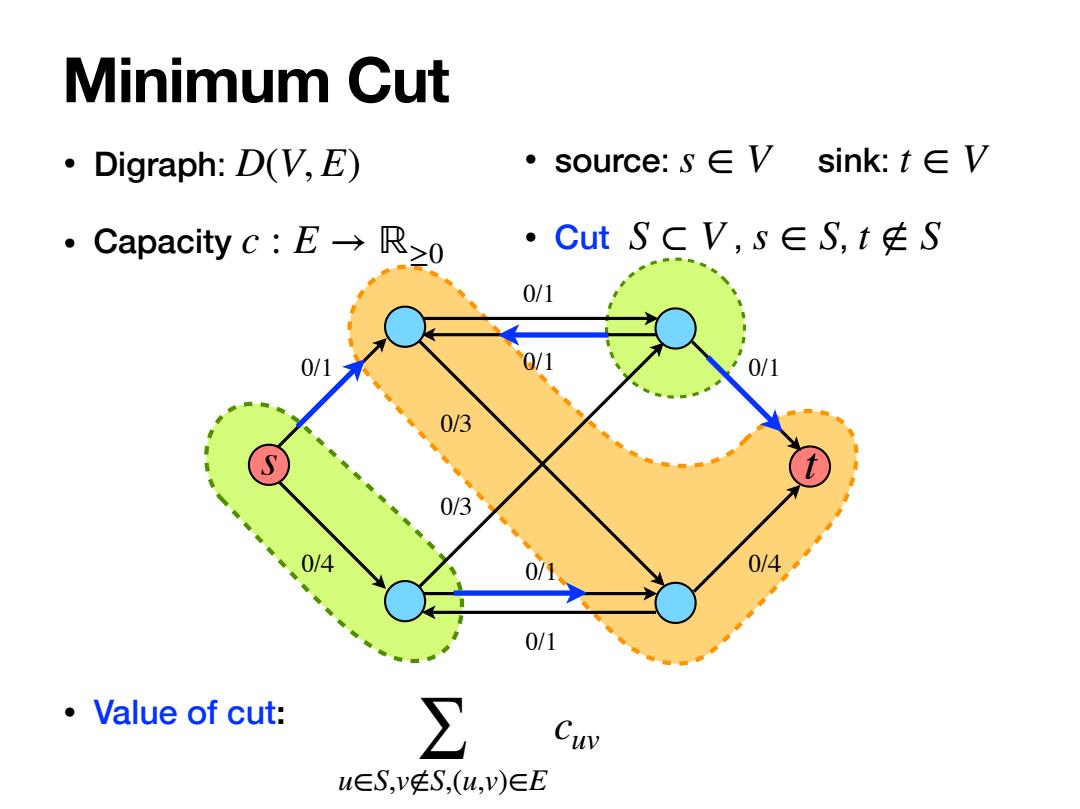
Minimum Cut ·Digraph:D(V,E) ·source:S∈V sink:t∈V ·Capacity c:E→R≥o ·Cut SCV,S∈S,t庄S 0/1 0/1 0/3 0/3 0/4 0/1 。Value of cut: Σ Cuv u∈S,v庄S,(u,v)∈E
• Digraph: • Capacity D(V, E) c : E → ℝ≥0 Minimum Cut 0/1 0/4 0/1 0/1 0/1 0/1 0/1 0/4 0/3 0/3 s t • source: sink: • Cut , , s ∈ V t ∈ V S ⊂ V s ∈ S t ∉ S • Value of cut: ∑ u∈S,v∉S,(u,v)∈E cuv
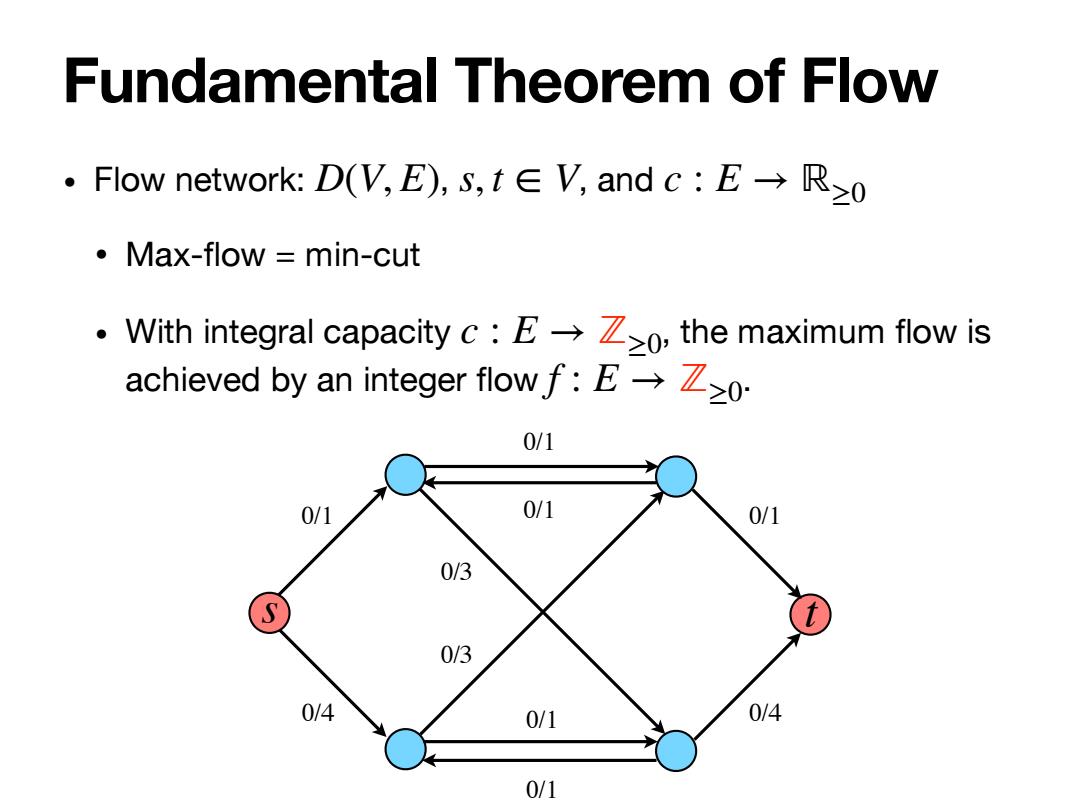
Fundamental Theorem of Flow .Flow network:D(V,E),s,t∈V,andc:E→R≥o 。Max-flow=min-cut 。With integral capacity c:E→Z≥o,the maximum flow is achieved by an integer flow f:E→Z≥o 0/1 0/1 0/1 0/1 0/3 S t 0/3 0/4 0/1 0/4 0/1
• Flow network: , , and • Max-flow = min-cut • With integral capacity , the maximum flow is achieved by an integer flow . D(V, E) s, t ∈ V c : E → ℝ≥0 c : E → ℤ≥0 f : E → ℤ≥0 Fundamental Theorem of Flow 0/1 0/4 0/1 0/1 0/1 0/1 0/1 0/4 0/3 0/3 s t
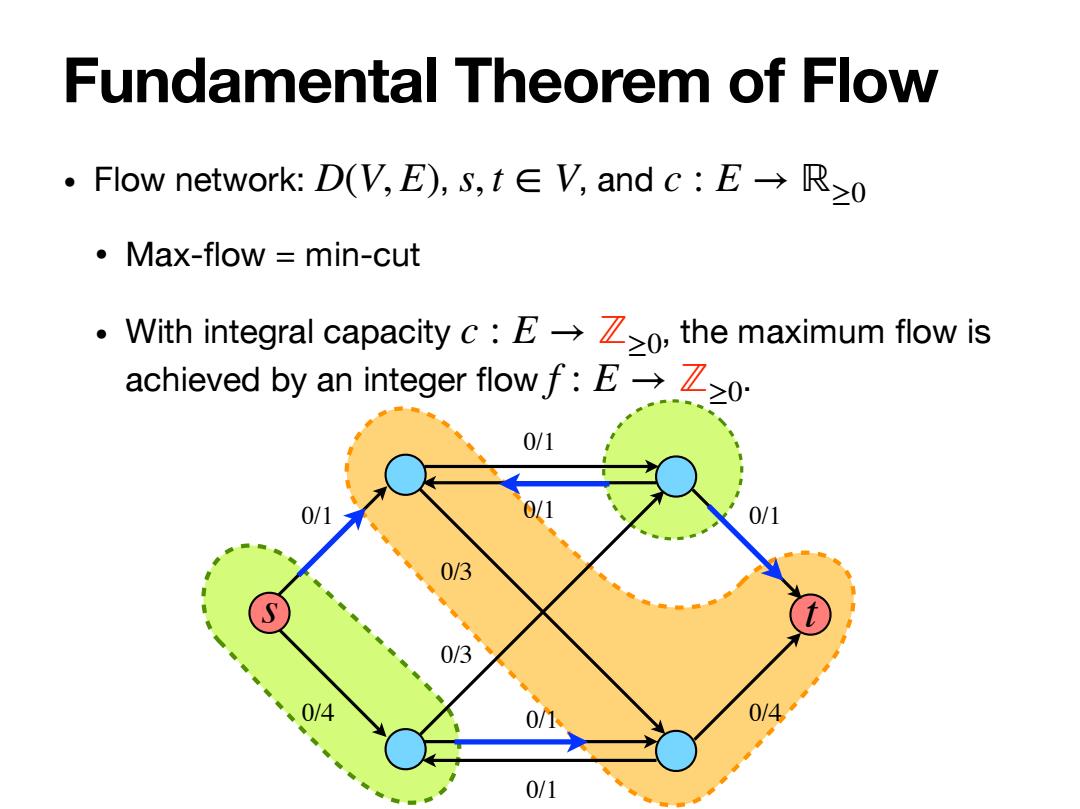
Fundamental Theorem of Flow .Flow network:D(V,E),s,t∈V,andc:E→R≥0 ·Max-flow=min-cut 、With integral capacity c:E→Z≥o,the maximum flow is achieved by an integer flow f:E→Z≥o- 0/1 01 0/1 0/3 S 0/3 0/4 0/1
• Flow network: , , and • Max-flow = min-cut • With integral capacity , the maximum flow is achieved by an integer flow . D(V, E) s, t ∈ V c : E → ℝ≥0 c : E → ℤ≥0 f : E → ℤ≥0 Fundamental Theorem of Flow s t 0/1 0/4 0/1 0/1 0/1 0/1 0/1 0/4 0/3 0/3

Fundamental Theorem of Flow .Flow network:D(V,E),s,t∈V,andc:E→R≥0 。Max-flow=min-cut 。With integral capacity c:E→Z≥o,the maximum flow is achieved by an integer flowf:E→Z≥o- 0/1 1/1 1/1 2/3 S 23 314 1/1 3/4 01
• Flow network: , , and • Max-flow = min-cut • With integral capacity , the maximum flow is achieved by an integer flow . D(V, E) s, t ∈ V c : E → ℝ≥0 c : E → ℤ≥0 f : E → ℤ≥0 Fundamental Theorem of Flow s t 1/1 3/4 0/1 1/1 1/1 0/1 1/1 3/4 2/3 2/3