
本次课主要内容 网络的容错性参数 (一)、连通度的概念与性质 (二)、描述连通性的其它参数简介(内容拓展
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (一)、连通度的概念与性质 (二)、描述连通性的其它参数简介(内容拓展) 网络的容错性参数

(一)、连通度的概念与性质 1、点连通度与边连通度的概念 定义1给定连通图G,设V©,若GV不连通, 称V为G的一个点割集,含有k个顶点的点割集 称为k顶点割。G中点数最少的顶点割称为最小顶点割。 例如: G2 在G中:{y3},,{v5,V3),{vs,V4}等是点割集。 在G,中没有点割集
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 1、点连通度与边连通度的概念 定义1 给定连通图G,设 ,若G -V' 不连通, 称V'为G的一个点割集,含有k个顶点的点割集 称为k顶点割。G中点数最少的顶点割称为最小顶点割。 例如: (一)、连通度的概念与性质 V VG ( ) G1 v5 v4 v3 v2 v1 v6 G2 v3 v4 v v2 1 在G1中:{v3}, {v5, v3}, {v5, v4}等是点割集。 在G2中没有点割集
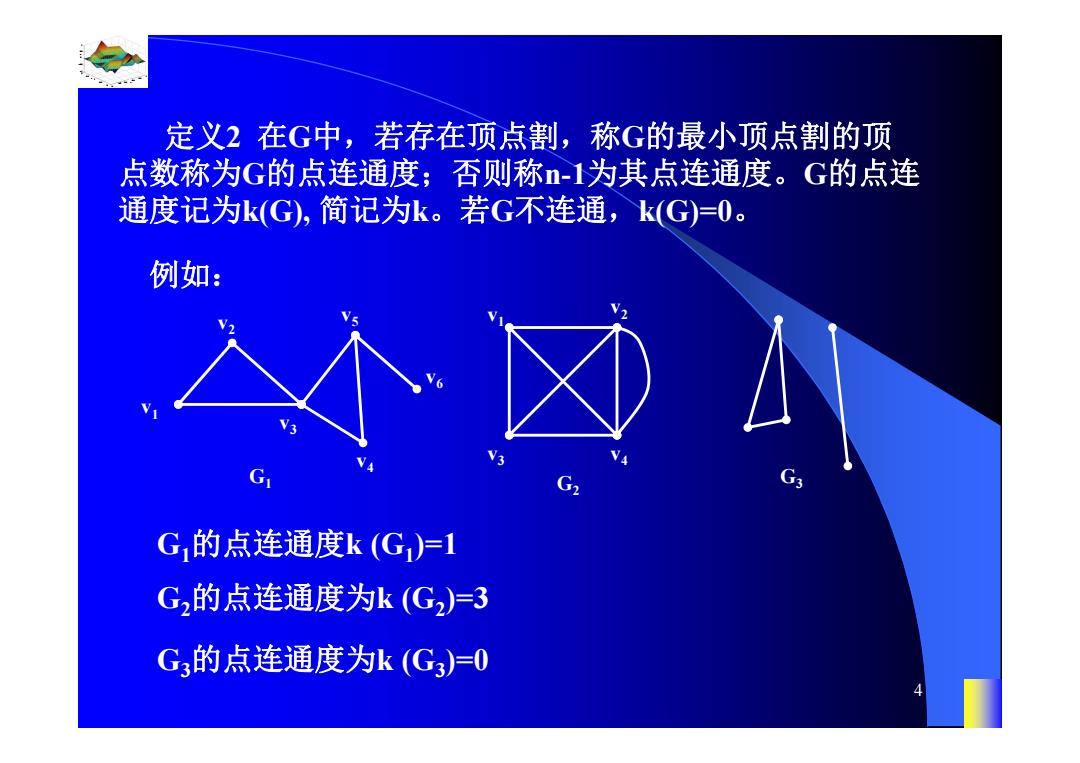
定义2在G中,若存在顶点割,称G的最小顶点割的顶 点数称为G的点连通度;否则称-1为其点连通度。G的点连 通度记为k(G),简记为k。若G不连通,k(G)=0。 例如: G,的点连通度k(G)=1 G,的点连通度为k(G2)=3 G3的点连通度为k(G3)=0
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 定义2 在G中,若存在顶点割,称G的最小顶点割的顶 点数称为G的点连通度;否则称n-1为其点连通度。G的点连 通度记为k(G), 简记为k。若G不连通,k(G)=0。 例如: G1 v5 v4 v3 v2 v1 v6 G2 v3 v4 v v2 1 G1的点连通度k (G1)=1 G2的点连通度为k (G2)=3 G3 G3的点连通度为k (G3)=0
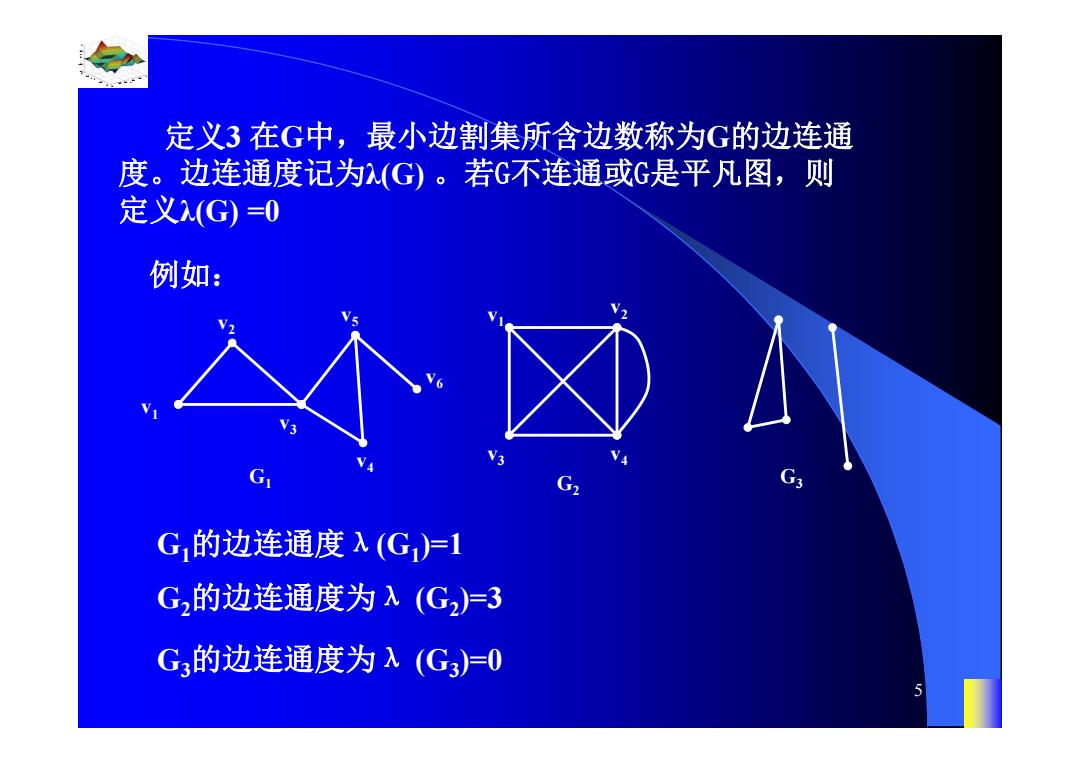
定义3在G中,最小边割集所含边数称为G的边连通 度。边连通度记为(G)。若G不连通或G是平凡图,则 定义(G)=0 例如: G,的边连通度λ(G)=1 G,的边连通度为λ(G,)=3 G的边连通度为入(G3)=0
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 定义3 在G中,最小边割集所含边数称为G的边连通 度。边连通度记为λ(G) 。若G不连通或G是平凡图,则 定义λ(G) =0 例如: G1 v5 v4 v3 v2 v1 v6 G2 v3 v4 v v2 1 G1的边连通度λ(G1)=1 G2的边连通度为λ (G2)=3 G3 G3的边连通度为λ (G3)=0
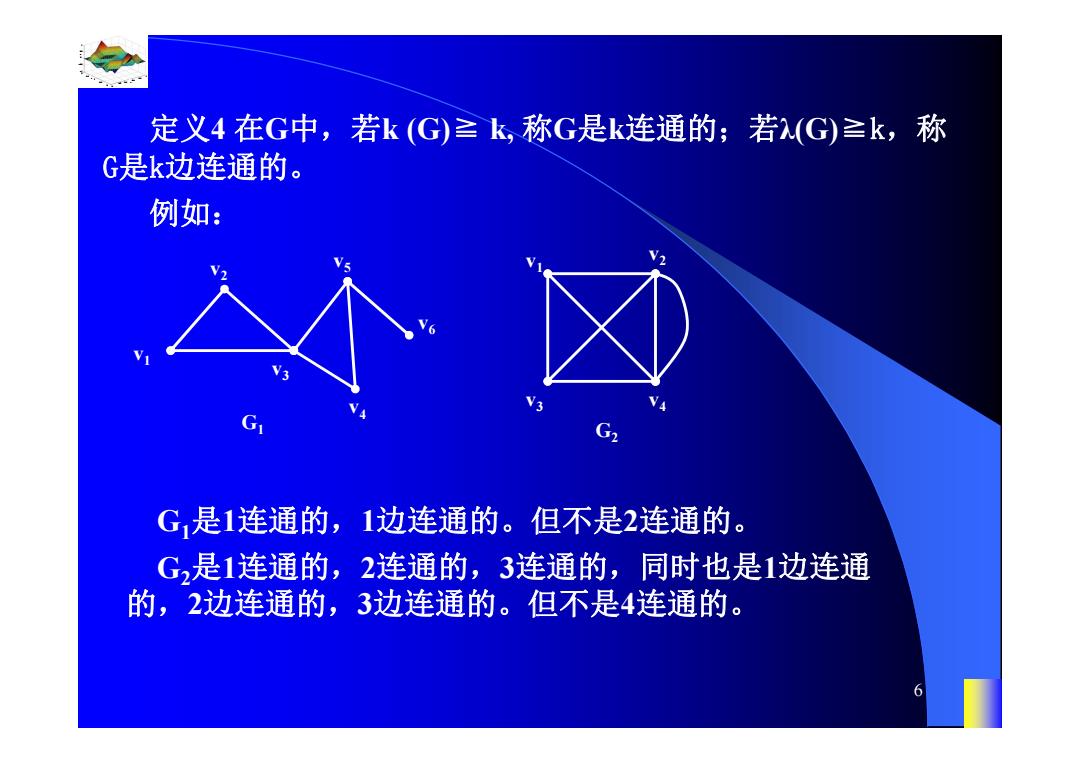
定义4在G中,若k(G)≥k,称G是k连通的;若(G)≥k,称 G是k边连通的。 例如: G,是1连通的,1边连通的。但不是2连通的。 G,是1连通的,2连通的,3连通的,同时也是1边连通 的,2边连通的,3边连通的。但不是4连通的
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 定义4 在G中,若k (G)≧ k, 称G是k连通的;若λ(G)≧k,称 G是k边连通的。 例如: G1 v5 v4 v3 v2 v1 v6 G2 v3 v4 v v2 1 G1是1连通的,1边连通的。但不是2连通的。 G2是1连通的,2连通的,3连通的,同时也是1边连通 的,2边连通的,3边连通的。但不是4连通的
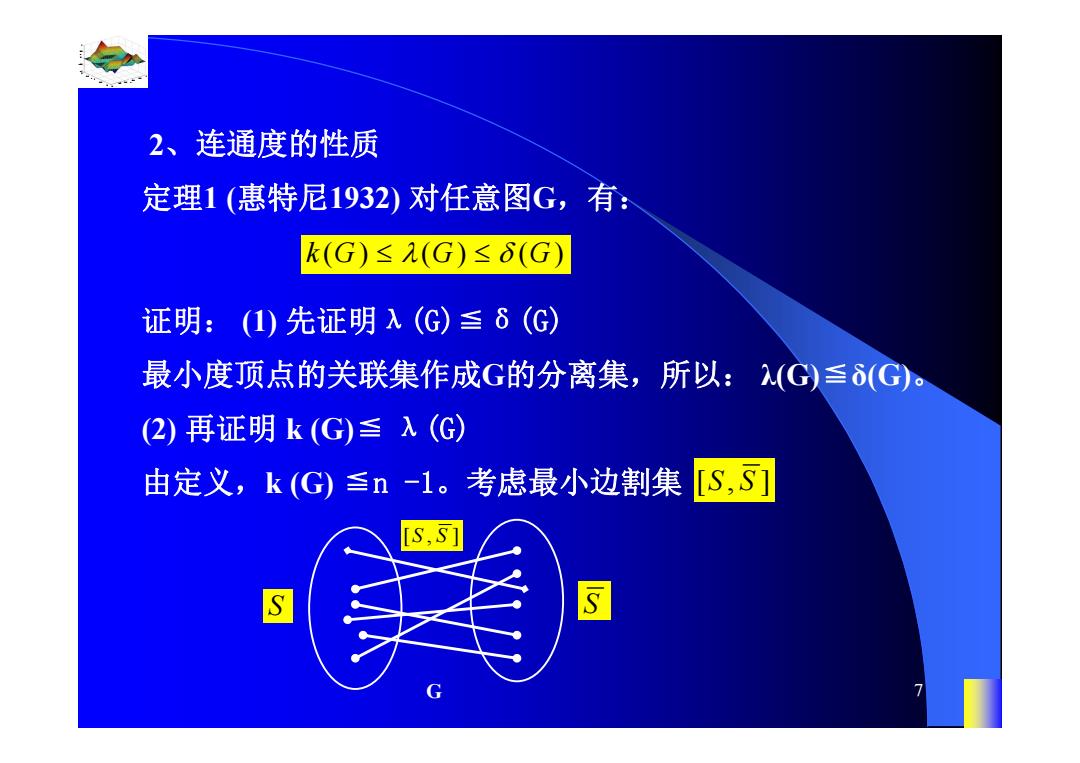
2、连通度的性质 定理1(惠特尼1932)对任意图G,有: k(G)≤(G)≤6(G) 证明:(1)先证明λ(G)至δ(G) 最小度顶点的关联集作成G的分离集,所以:(G)≤δ(G)。 (2)再证明k(G)≤λ(G) 由定义,k(G)≤n-1。考虑最小边割集 [S,S] [S,S] S
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 2、连通度的性质 定理1 (惠特尼1932) 对任意图G,有: kG G G () () () 证明: (1) 先证明λ(G)≦δ(G) 最小度顶点的关联集作成G的分离集,所以: λ(G)≦δ(G)。 (2) 再证明 k (G)≦ λ(G) 由定义,k (G) ≦n -1。考虑最小边割集 [, ] S S S S [, ] S S G
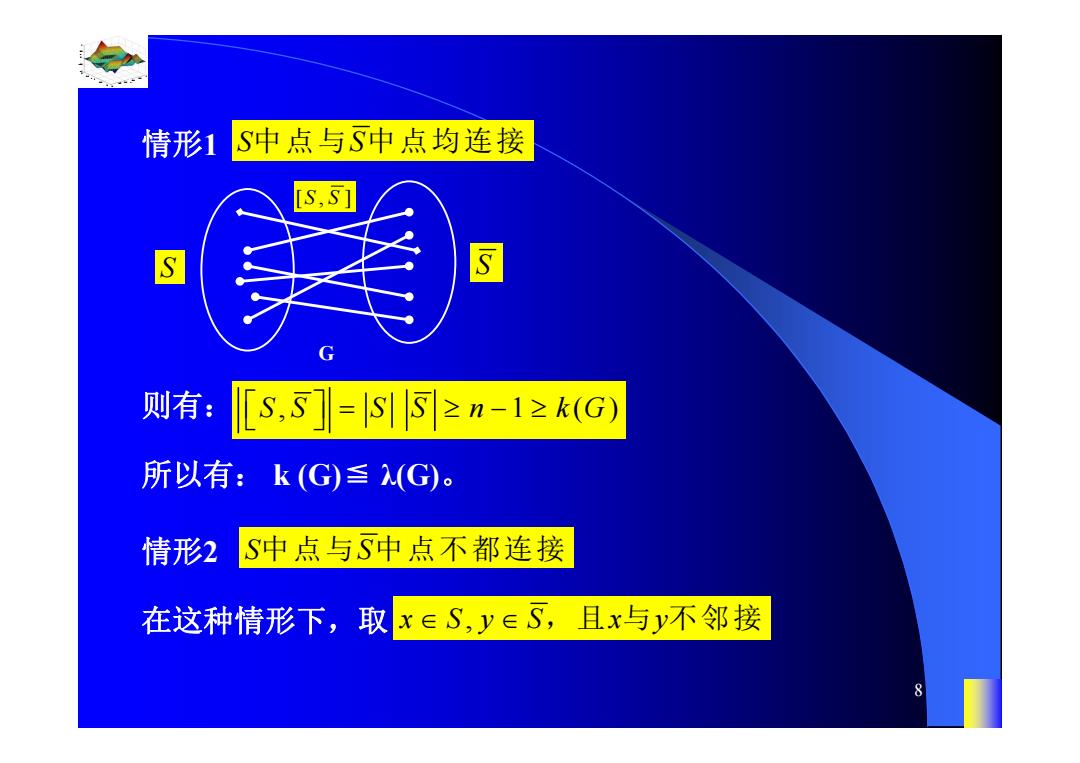
情形1 S中点与S中点均连接 [S,S] 则有: [s,s]=l小S≥n-1≥kG) 所以有:k(G)≤(G。 情形2 S中点与S中点不都连接 在这种情形下,取x∈S,y∈S,且x与y不邻接 8
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 情形1 则有: S S [, ] S S G S S 中点与 中点均连接 SS S S n kG , 1 () 所以有: k (G)≦ λ(G)。 情形2 S S 中点与 中点不都连接 在这种情形下,取 x Sy S x y , ,且 与 不邻接
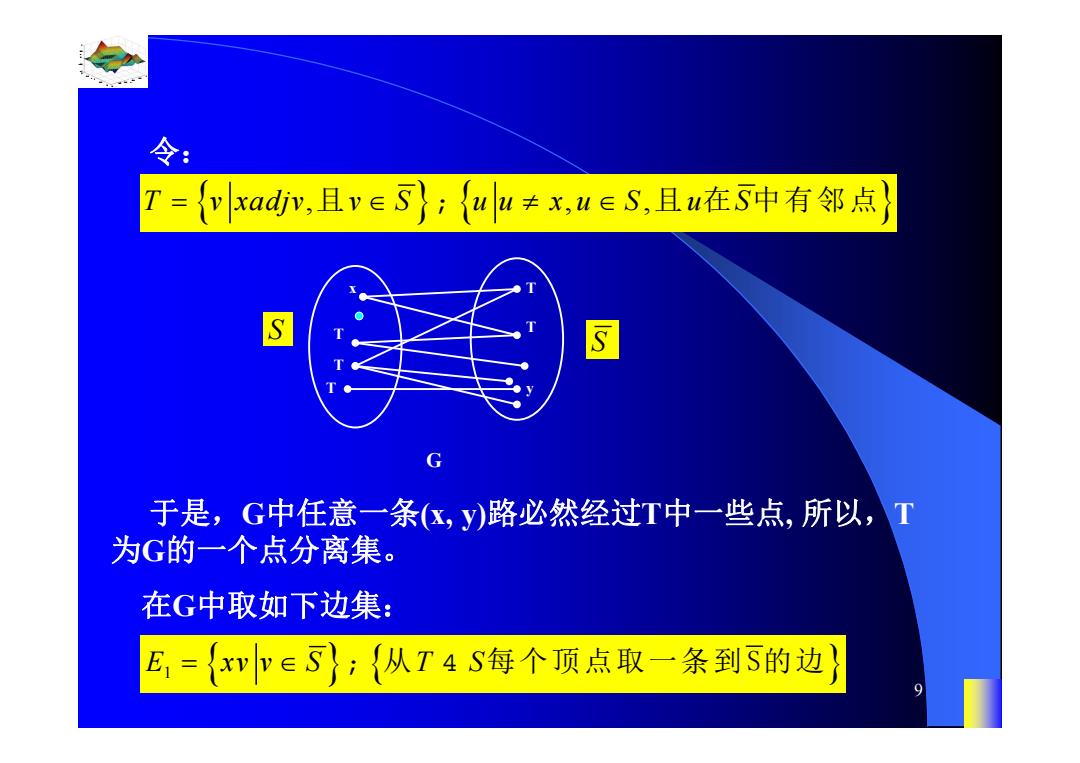
令: 7={ykad,且veS}:{ulu≠x,u∈S,且u在S中有邻点 于是,G中任意一条(区,y)路必然经过T中一些点,所以,T 为G的一个点分离集。 在G中取如下边集: E,={xp∈S;{从T4S每个顶点取一条到S的边
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 令: T v xadjv v S u u x u S u S , ,, 且 且 在 中有邻点 U 于是,G中任意一条(x, y)路必然经过T中一些点, 所以,T 为G的一个点分离集。 S S G T T x T T T y 在G中取如下边集: E xv v S T S 1 U I 从 每个顶点取一条到 S的边
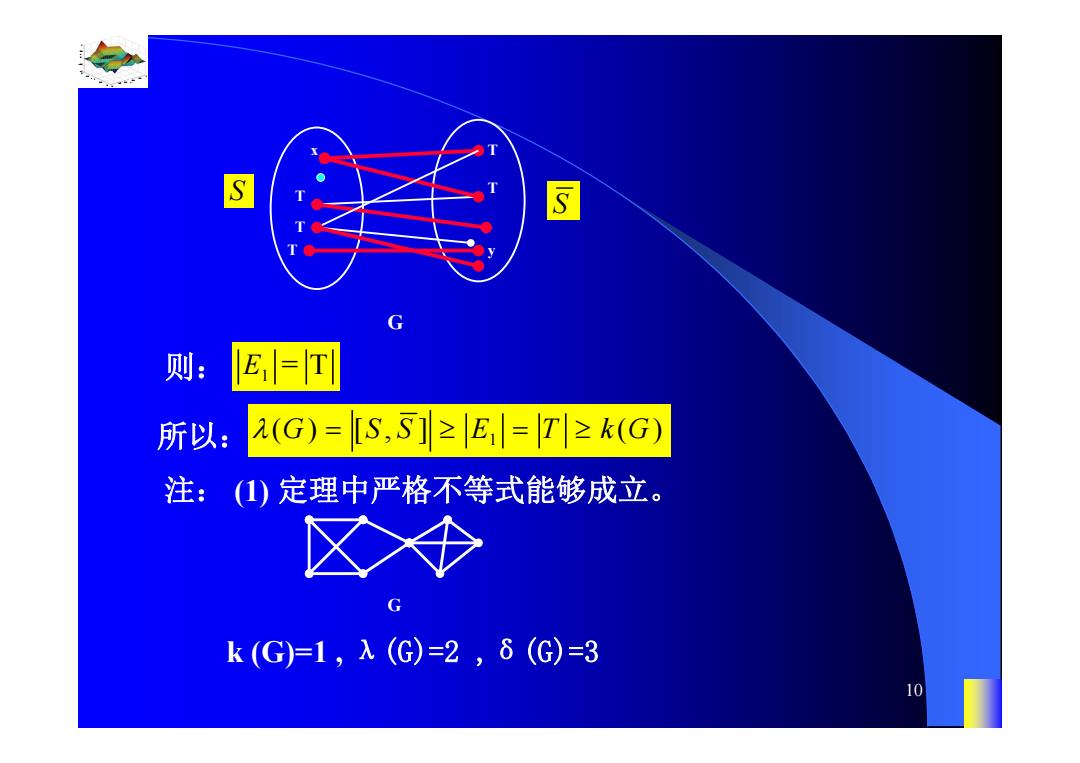
S 则: ll= 所以: (G)=[S,S]≥E=T≥k(G) 注:(I)定理中严格不等式能够成立。 G k(G)=1,λ(G)=2,δ(G)=3 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 则: S S G T T x T T T y 所以: E1 = T 1 ( ) [, ] ( ) G SS E T kG 注: (1) 定理中严格不等式能够成立。 k (G)=1 , λ(G)=2 ,δ(G)=3 G

(2)定理中等式能够成立。 G k(G)=λ(G)=δ(G)=2 (③)哈拉里通过构图的方式已经证明: 对任意正整数a,b,c,都存在图G,使得: k(G)=a,(G)=b,δ(G)=c (4)惠特尼(1907--1989)美国著名数学家。主要研究图论 与拓扑学。先后分别在哈佛和普林斯顿高级研究院工作。他 获过美国国家科学奖(1976),Wolf奖(1983),Steel奖(1985)
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 (2) 定理中等式能够成立。 k (G)=λ(G)= δ(G)=2 G (3) 哈拉里通过构图的方式已经证明: 对任意正整数a, b, c,都存在图G,使得: kG a G b G c () ,() ,() (4) 惠特尼(1907---1989)美国著名数学家。主要研究图论 与拓扑学。先后分别在哈佛和普林斯顿高级研究院工作。他 获过美国国家科学奖(1976),Wolf奖(1983),Steel奖(1985)