
本次课主要内容 最小生成树 (一、克鲁斯克尔算法 (二)、管梅谷的破圈法 (三)、Prim算法 (四)、根树简介
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 最小生成树 (一)、克鲁斯克尔算法 (二)、管梅谷的破圈法 (三)、Prim算法 (四)、根树简介

最小连接问题: 交通网络中,常常关注能把所有站点连接起来的生 成树,使得该生成树各边权值之和为最小。例如: 假设要在某地建造5个工厂,拟修筑道路连接这5处。 经勘探,其道路可按下图的无向边铺设。现在每条边的 长度已经测出并标记在图的对应边上,如果我们要求铺 设的道路总长度最短,这样既能节省费用,又能缩短 工期,如何铺设?
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 最小连接问题: 交通网络中,常常关注能把所有站点连接起来的生 成树,使得该生成树各边权值之和为最小。例如: 假设要在某地建造5个工厂,拟修筑道路连接这5处。 经勘探,其道路可按下图的无向边铺设。现在每条边的 长度已经测出并标记在图的对应边上,如果我们要求铺 设的道路总长度最短,这样既能节省费用 ,又能缩短 工期 ,如何铺设? v1 v2 v3 v4 v5 1 2 4 3 2 4 5 5

不难发现:最小代价的连接方式为: 最小连接问题的一般提法为: 在连通边赋权图G中求一棵总权值最小的生成树。 该生成树称为最小生成树或最小代价树。 (一)、克鲁斯克尔算法
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 v1 v2 v3 v4 v5 1 2 2 3 不难发现:最小代价的连接方式为: 最小连接问题的一般提法为: 在连通边赋权图G中求一棵总权值最小的生成树。 该生成树称为最小生成树或最小代价树。 (一)、克鲁斯克尔算法

克鲁斯克尔(Kruskal):1928年生,一家3弟兄都是数学家, 1954年在普林斯顿大学获博士学位,导师是Erd0s,他 大部分研究工作是数学和语言学,主要在贝尔实验室工 作。1956年发表包含克鲁斯克尔算法论文,使他名声大 振。 1、算法思想 从G中的最小边开始,进行避圈式扩张。 2、算法 (1)、选择边e,使得其权值最小: (2)、若已经选定边e1,2,k,则从E-{e1,e2,,C} 中选择边ek+1,使得: (a小Ge,e2,ek+l为无圈图 (b)、ek+1的权值w(ek+)尽可能小
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 克鲁斯克尔(Kruskal):1928年生,一家3弟兄都是数学家, 1954年在普林斯顿大学获博士学位,导师是ErdÖs,他 大部分研究工作是数学和语言学,主要在贝尔实验室工 作。1956年发表包含克鲁斯克尔算法论文,使他名声大 振。 1、算法思想 从G中的最小边开始,进行避圈式扩张。 2、算法 (1)、选择边e1,使得其权值最小; (2)、若已经选定边e1, e2,…, ek, 则从E-{ e1, e2,…, ek } 中选择边ek+1,使得: (a)、G[e1, e2,…, ek+1]为无圈图 (b)、ek+1的权值w(ek+1)尽可能小
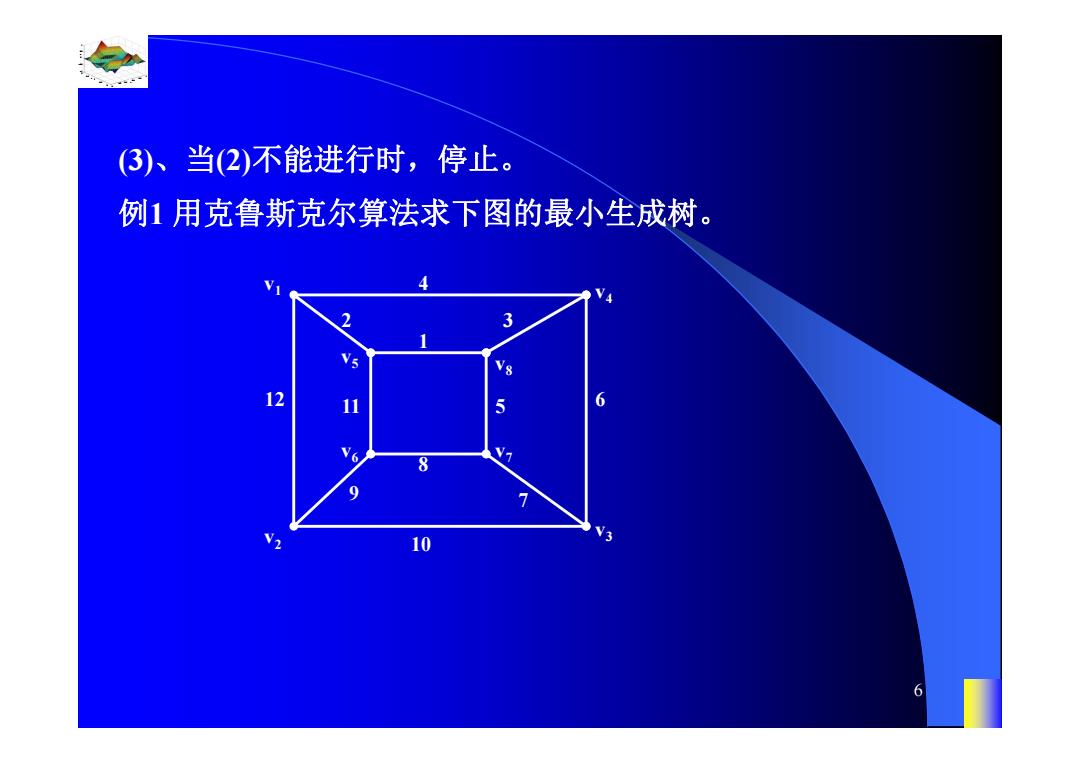
(3)、当(2)不能进行时,停止。 例1用克鲁斯克尔算法求下图的最小生成树。 3 12 6 10 6
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 (3)、当(2)不能进行时,停止。 例1 用克鲁斯克尔算法求下图的最小生成树。 3 v7 2 1 5 4 6 7 8 9 10 11 12 v1 v2 v3 v4 v5 v6 v8

解:过程如下: 3 Vs 3 3 5 5 5 6 7
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 解:过程如下: 1 v5 v8 2 1 v1 v5 v8 2 3 1 v1 v4 v5 v8 3 v7 2 1 5 v1 v4 v5 v8 3 v7 2 1 5 6 v1 v4 v5 v8 v3

6 6 8 定理1由克鲁斯克尔算法得到的任何生成树一定是最小 生成树。(证明略) 8
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 3 v7 2 1 5 6 v1 v4 v5 v8 v3 v6 8 3 v7 2 1 5 6 v1 v4 v5 v8 v3 v6 8 v2 9 定理1 由克鲁斯克尔算法得到的任何生成树一定是最小 生成树。(证明略)

例2在一个边赋权G中,下面算法是否可以产生有最小 权值的生成路?为什么? 算法:(I)选一条边e,使得w(e)尽可能小; (2)若边e1,e2…,e已经选定,则用下述方法从D(e1,e;}中 选取边e+1: (a)G(e1e2,e:,et1)]为不相交路之并; (b)w(e+i)是满足(a)的尽可能小的权。 (3)当(2)不能继续执行时停止。 解:该方法不能得到一条最小生成路
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 例2 在一个边赋权G中,下面算法是否可以产生有最小 权值的生成路?为什么? 算法: (1) 选一条边e1,使得w(e1)尽可能小; (2) 若边e1,e2,…,ei已经选定,则用下述方法从E\{e1,..,ei}中 选取边ei+1: (a) G[{ e1,e2,…,ei ,ei+1}]为不相交路之并; (b) w(ei+1)是满足(a)的尽可能小的权。 (3)当 (2)不能继续执行时停止。 解:该方法不能得到一条最小生成路

例如,在下图G中我们用算法求生成路: 用算法求出的生成路为: 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 例如,在下图G中我们用算法求生成路: 3 1 2 2 3 4 3 6 6 7 9 10 用算法求出的生成路为: 1 2 2 6 9 3

直接在图中选出的一条生成路为: 后者的权值小于前者。 (二)、管梅谷的破圈法 在克鲁斯克尔算法基础上,我国著名数学家管梅谷 教授于1975年提出了最小生成树的破圈法
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 直接在图中选出的一条生成路为: 1 2 3 3 6 6 后者的权值小于前者。 (二)、管梅谷的破圈法 在克鲁斯克尔算法基础上,我国著名数学家管梅谷 教授于1975年提出了最小生成树的破圈法