
本次课主要内容 拉姆齐问题简介 (一) 独立集与覆盖 (二)、 边独立集与边覆盖 (三)、点临界图与边临界图 (四)、拉姆齐数r(m,n)
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (二)、边独立集与边覆盖 拉姆齐问题简介 (一)、 独立集与覆盖 (四)、拉姆齐数r (m, n) (三)、点临界图与边临界图

(一)、独立集与覆盖 1、概念 定义1设G=(V,E)是一个图。V的一个非空顶点子集V 称为G的一个点独立集,如果V,中的顶点互不邻接; G的一个包含顶点数最多的独立集称为G的最大独立集。 最大独立集包含的顶点数,称为G的点独立数,记为α(G) G的一个独立集 G的一个最大独立集
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 1、概念 定义1 设G=(V ,E)是一个图。V的一个非空顶点子集V1 称为G的一个点独立集,如果V1中的顶点互不邻接; (一)、独立集与覆盖 G的一个包含顶点数最多的独立集称为G的最大独立集。 最大独立集包含的顶点数,称为G的点独立数,记为α(G)。 v v2 1 v6 v5 v4 v3 v7 v8 G的一个独立集 v v2 1 v6 v5 v4 v3 v7 v8 G的一个最大独立集
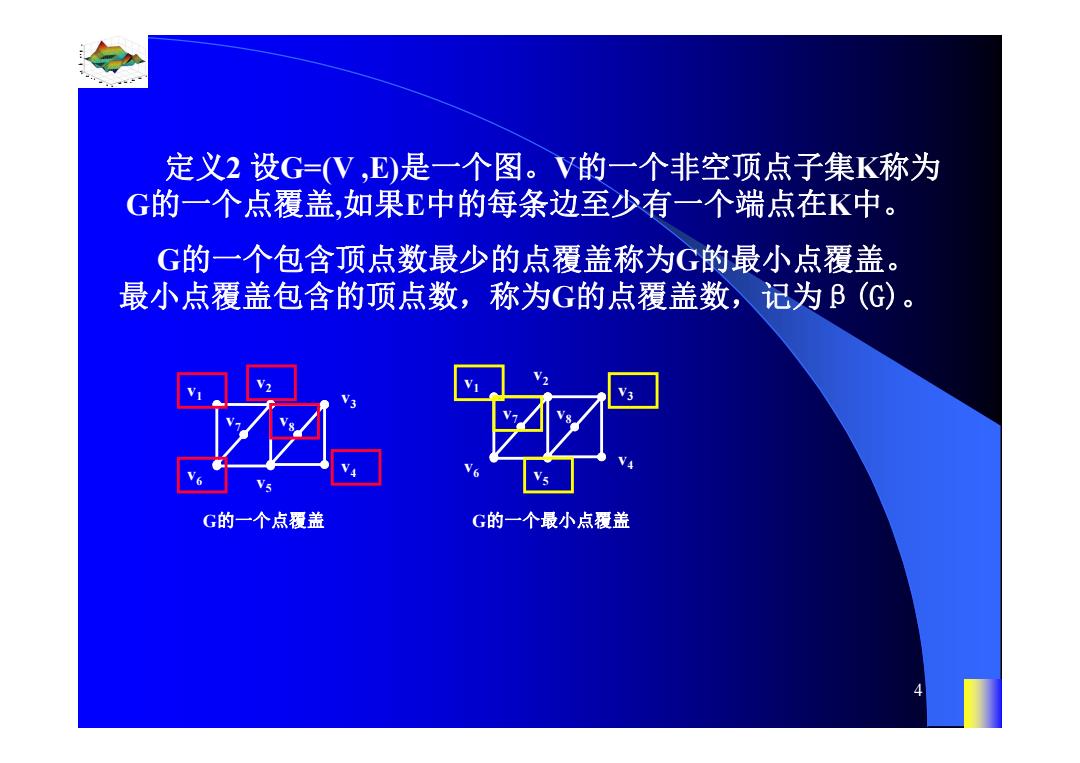
定义2设G=V,E)是一个图。V的一个非空顶点子集K称为 G的一个点覆盖,如果E中的每条边至少有一个端点在K中。 G的一个包含顶点数最少的点覆盖称为G的最小点覆盖。 最小点覆盖包含的顶点数,称为G的点覆盖数,记为B(G)。 G的一个点覆盖 G的一个最小点覆盖
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 定义2 设G=(V ,E)是一个图。V的一个非空顶点子集K称为 G的一个点覆盖,如果E中的每条边至少有一个端点在K中。 G的一个包含顶点数最少的点覆盖称为G的最小点覆盖。 最小点覆盖包含的顶点数,称为G的点覆盖数,记为β(G)。 v v2 1 v6 v5 v4 v3 v7 v8 G的一个最小点覆盖 v2 v6 v5 v4 v3 v7 v8 G的一个点覆盖 v1

2、加莱恒等式 定理1(加莱)对任意不含孤立点的n阶图G,有: a(G)+(G)=n 证明:一方面,设V,是G的最大点独立集。因为G中 每条边的端点最多一个在V中,所以G中每条边的端点 至少有一个在V-V中。即V-V构成G的一个点覆盖,于 是有: B(G)V-V =n-a(G) 另一方面,设K是G的最小点覆盖。因为G中每条边的 端点至少有一个在K中,所以G中每条边的端点至多有 个在V-K中。即V-K构成G的一个点独立集,于是有:
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 定理1 (加莱) 对任意不含孤立点的n阶图G,有: 2、加莱恒等式 α(G)+ β(G)= n 证明:一方面,设V1是G的最大点独立集。因为G中 每条边的端点最多一个在V1中,所以G中每条边的端点 至少有一个在V-V1中。即V-V1构成G的一个点覆盖,于 是有: β(G)≦|V-V1|=n - α(G) 另一方面,设K是G的最小点覆盖。因为G中每条边的 端点至少有一个在K中,所以G中每条边的端点至多有一 个在V-K中。即V-K构成G的一个点独立集,于是有:

a(G≥1V-K|=n-(G) 由上面两个不等式,得到: α(G+(G)=n (二)、边独立集与边覆盖 1、概念 定义3设G=(V,E)是一个图。E的一个边子集E,称为G 的一个边独立集,如果E,中的边互不邻接; G的一个包含边数最多的边独立集称为G的最大边独立 集。最大边独立集包含的边数,称为G的边独立数,记为 m'(G
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 α(G) ≥|V-K|=n - β(G) 由上面两个不等式,得到: α(G)+ β(G)= n (二)、边独立集与边覆盖 1、概念 定义3 设G=(V ,E)是一个图。E的一个边子集E1称为G 的一个边独立集,如果E1中的边互不邻接; G的一个包含边数最多的边独立集称为G的最大边独立 集。最大边独立集包含的边数,称为G的边独立数,记为 α‵(G)

G的一个边独立集 G的一个最大边独立集 注:单图的一个边独立集实际上就是图的个匹配, 一个最大边独立集就是其一个最大匹配。 定义4设G=V,E)是一个图。E的一个边子集L称为G的 一个边覆盖,如果G中的每个顶点均是L中某条边的端点。 G的一个包含边数最少的边覆盖称为G的最小边覆盖。最 小边覆盖包含的边数,称为G的边覆盖数,记为邹(G)
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 注:单图的一个边独立集实际上就是图的一个匹配, 一个最大边独立集就是其一个最大匹配。 G的一个边独立集 G的一个最大边独立集 定义4 设G=(V ,E)是一个图。E的一个边子集 L 称为G的 一个边覆盖,如果G中的每个顶点均是L中某条边的端点。 G的一个包含边数最少的边覆盖称为G的最小边覆盖。最 小边覆盖包含的边数,称为G的边覆盖数,记为β‵(G)
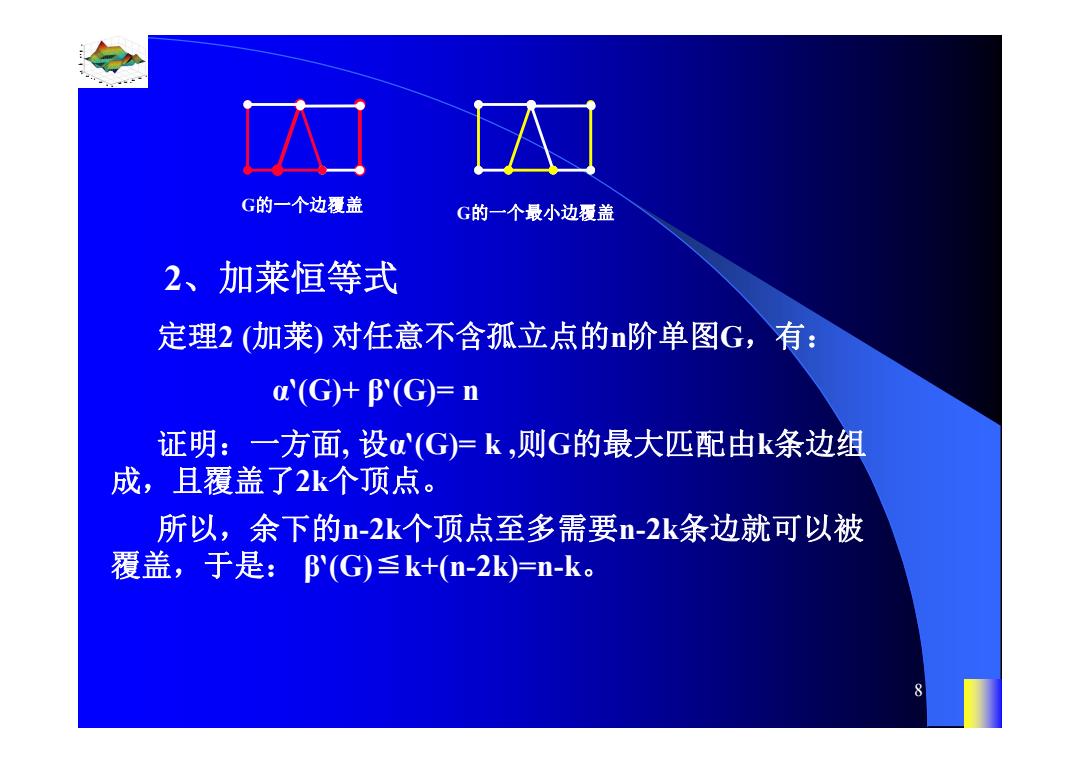
G的一个边覆盖 G的一个最小边覆盖 2、加莱恒等式 定理2(加莱)对任意不含孤立点的阶单图G,有: a(G)+(G)=n 证明:一方面,设α(G)=k,则G的最大匹配由k条边组 成,且覆盖了2k个顶点。 所以,余下的m-2k个顶点至多需要-2k条边就可以被 覆盖,于是:(G)≤k+(n-2k)=-k
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 G的一个边覆盖 G的一个最小边覆盖 2、加莱恒等式 定理2 (加莱) 对任意不含孤立点的n阶单图G,有: α‵(G)+ β‵(G)= n 证明:一方面, 设α‵(G)= k ,则G的最大匹配由k条边组 成,且覆盖了2k个顶点。 所以,余下的n-2k个顶点至多需要n-2k条边就可以被 覆盖,于是: β‵(G)≦k+(n-2k)=n-k

所以,m(G)+(G)≤k+(m-k)尸n 另一方面,设X是G的一个最小边覆盖,则IX|=(G)。 考虑导出子图F=GX。可以证明F中不会包含长度为3的迹。 若不然,设F中包含长度为3的迹。取该迹的中间边e,显 然,X-e仍然构成G的边覆盖,与X的最小性矛盾。 所以,F中不包含长度为3和大于3的迹。也不包含圈。 所以,F中的每个连通分支必然为星图。F是森林。 因为,阶数为n,边数为m-k的森林包含k个连通分支。 而F的边数为n-(n-(G),所以F有n-(G)个分支
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 所以,α‵(G)+ β‵(G)≦ k+ (n - k)= n 另一方面, 设X是G的一个最小边覆盖,则 |X|= β‵(G)。 考虑导出子图F = G[X]。可以证明F中不会包含长度为3的迹。 若不然,设F中包含长度为3的迹。取该迹的中间边e,显 然,X-e仍然构成G的边覆盖,与X的最小性矛盾。 所以,F中不包含长度为3和大于3的迹。也不包含圈。 所以,F中的每个连通分支必然为星图。F是森林。 因为,阶数为n,边数为n-k的森林包含k个连通分支。 而F的边数为n - (n- β‵(G)) ,所以F有n- β‵(G)个分支

从F的每个分支中选取一条边,可作成G的一个匹配, 所以a(G)≥n-(G)。 由上面两个不等式,得到:a(G)+G)=n。 例1确定下图G的a(G),(G),a(G),(G。 G 解:顶点2的左右两部分均是K,所以可以推知α(G)=2, 再由加莱恒等式得:(G)=5。 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 从F的每个分支中选取一条边,可作成G的一个匹配, 所以α‵(G) ≥ n- β‵(G)。 由上面两个不等式,得到: α‵(G)+ β‵(G)= n。 例1 确定下图G的 α(G), β(G), α‵(G) , β‵(G)。 1 4 3 2 5 6 7 G 解:顶点2的左右两部分均是K4, 所以可以推知α(G)=2, 再由加莱恒等式得: β(G) = 5
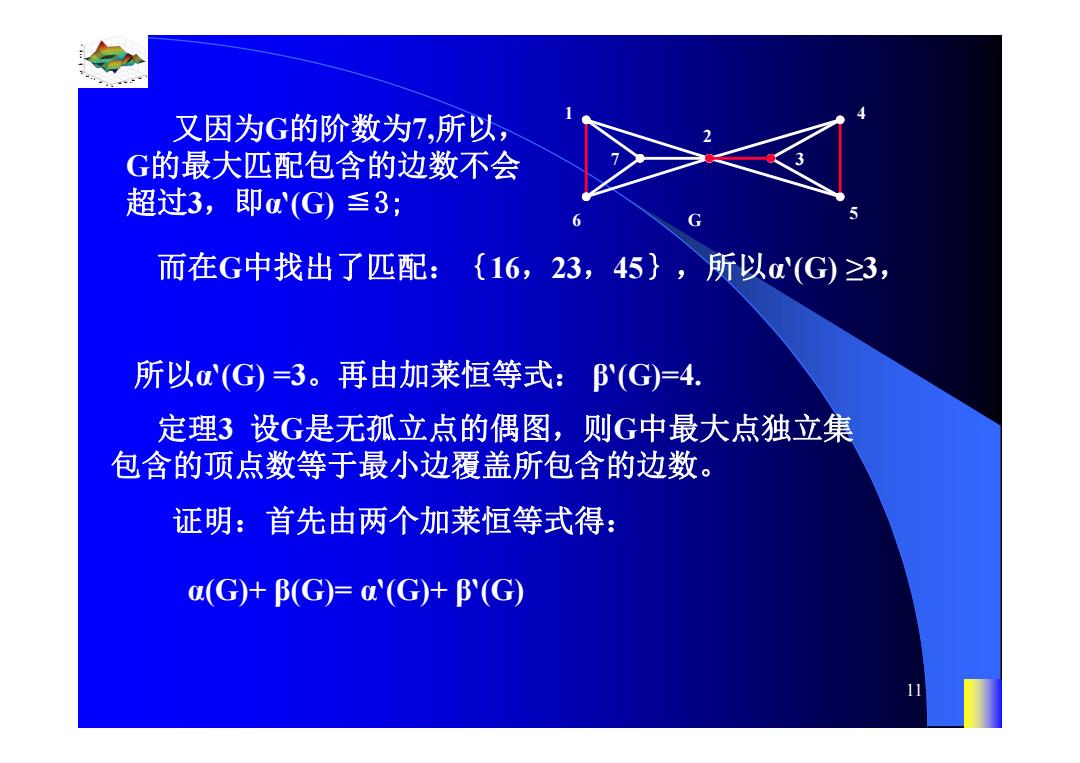
又因为G的阶数为7,所以, G的最大匹配包含的边数不会 超过3,即m(G)≤3; 而在G中找出了匹配:{16,23,45},所以α(G)≥3, 所以(G)=3。再由加莱恒等式: '(G)=4. 定理3设G是无孤立点的偶图,则G中最大点独立集 包含的顶点数等于最小边覆盖所包含的边数。 证明:首先由两个加莱恒等式得: α(G)+(G)=Q'(G)+(G
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 定理3 设G是无孤立点的偶图,则G中最大点独立集 包含的顶点数等于最小边覆盖所包含的边数。 1 4 3 2 5 6 7 G 又因为G的阶数为7,所以, G的最大匹配包含的边数不会 超过3,即α‵(G) ≦3; 而在G中找出了匹配:{16,23,45},所以α‵(G) ≥3, 所以α‵(G) =3。再由加莱恒等式: β‵(G)=4. 证明:首先由两个加莱恒等式得: α(G)+ β(G)= α‵(G)+ β‵(G)