
本次课主要内容 度极大非哈密尔顿图与TSP问题 (一)、度极大非哈密尔顿图 (二)、TSP问题
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (一)、度极大非哈密尔顿图 (二)、TSP问题 度极大非哈密尔顿图与TSP问题

(一)、度极大非哈密尔顿图 1、定义 定义1图G称为度极大非H图,如果它的度不弱 于其它非H图。 2、Cmn图 定义2对于1≤m<n/2,Cmn图定义为: Cmn=KmV(区m+Kn2m〉 例如,作出C1s与C25
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 1、定义 (一)、度极大非哈密尔顿图 定义1 图G称为度极大非H图,如果它的度不弱 于其它非H图。 2、C m, n图 定义2 对于1≦ m <n/2 , C m, n 图定义为: , 2 ( ) C K KK mn m m n m 例如,作出C1,5与C2,5

图☒ K C25 3、Cn的性质 引理1对于1≤mS=m,所以, 由H图的性质知,G是非H图。 4、度极大非H图的特征
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 3、Cm, n的性质 K1 K1 K3 C1,5 K2 K2 K1 C2,5 引理1 对于1≦m |S|=m,所以, 由H图的性质知,G是非H图。 4、度极大非H图的特征

定理1(Chyatal,1972 若G是n≥3的非H单图,则G度弱于某个Cmn图。 证明:设G是度序列为(4,4,,dn)的非H单图, 且d1≤d2≤..≤dn,n≥3。 由度序列判定法:存在m<n/2,使得dm≤m,且dnm. 于是,G的度序列必弱于如下序列: n-2m (m,m,m,n-m-1,n-m-1,,n-m-1,n-1,n-l,,n-1 而上面序列正好是图Cm,的度序列。 注:(1)定理1刻画了非H单图的特征:从度序列角度 看,C%n图族中某个图是某个阶非H单图的极图
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 定理1 (Chvátal,1972) 若G是n≧3的非H单图,则G度弱于某个C m, n图。 证明: 设G是度序列为 (d1,d2,…,dn)的非H单图, 且d1≦d2≦…≦dn, n≧3。 由度序列判定法:存在m<n/2,使得dm≦m,且dn-m<n-m. 于是,G的度序列必弱于如下序列: 2 ( , ,..., , 1, 1,..., 1, 1, 1,..., 1 m nm m mm mn m n m n m n n n 64 7 48 6 4 4 4 44 7 4 4 4 4 48 6 4 447 4 448 而上面序列正好是图Cm,n的度序列。 注: (1) 定理1刻画了非H单图的特征:从度序列角度 看,Cm, n图族中某个图是某个n阶非H单图的极图
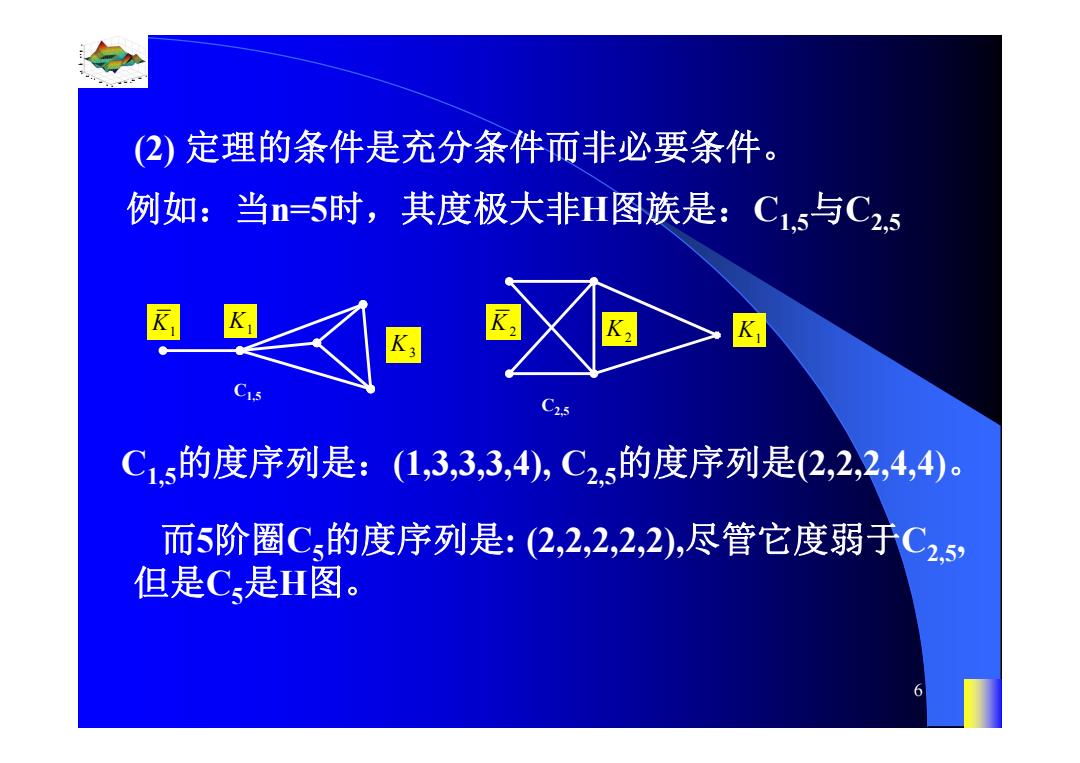
(2)定理的条件是充分条件而非必要条件。 例如:当n=5时,其度极大非H图族是:C1s与C25 K2 C1s的度序列是:(1,3,3,3,4),C25的度序列是(2,2,2,4,4)。 而5阶圈C的度序列是:(2,2,2,2,2),尽管它度弱于C25) 但是C是H图。 6
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 (2) 定理的条件是充分条件而非必要条件。 例如:当n=5时,其度极大非H图族是:C1,5与C2,5 K1 K1 K3 C1,5 K2 K2 K1 C2,5 C1,5的度序列是:(1,3,3,3,4), C2,5的度序列是(2,2,2,4,4)。 而5阶圈C5的度序列是: (2,2,2,2,2),尽管它度弱于C2,5, 但是C5是H图

(3)如果n阶单图G度优于所有的Cmn图族,则G 是H图。 例如: G G的度序列是(2,3,3,4,4),优于C1s的度序列 (1,3,3,3,4)和C2.s的度序列(2,2,2,4,4)。所以可以断 定G是H图。 推论设G是n阶单图。若n≥3且 E(G川
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 (3) 如果n阶单图G度优于所有的Cm, n图族,则G 是H图。 G的度序列是(2,3,3,4,4),优于C1,5的度序列 (1,3,3,3,4)和C2,5的度序列 (2,2,2,4,4)。所以可以断 定G是H图。 例如: G 推论 设G是n阶单图。若n≧3且 1 () 1 2 n E G

则G是H图;并且,具有个顶点 2 条边 的非H图只有C1n以及C2.5 证明:(1)先证明G是H图。 若不然,由定理1,G度弱于某个Cm,于是有: E(G川≤E(C.=[m2+(n-2m)(n-m-1)+m(n-1)] (”21-安(m-1Xm-2y-m-10a-2m-) 这与条件矛盾!所以G是H图
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 则G是H图;并且,具有n个顶点 条边 的非H图只有C1,n以及C2,5. 1 1 2 n 证明: (1) 先证明G是H图。 若不然,由定理1,G度弱于某个Cm, n ,于是有: 2 , 1 ( ) ( ) ( 2 )( 1) ( 1) 2 1 1 1 ( 1)( 2) ( 1)( 2 1) 2 2 1 1 . 2 EG EC m n m n m mn m n n m m m nm n 这与条件矛盾!所以G是H图

(2)对于Cn,有: E(o=l5c="2+1 除此之外,只有当m=2且n=5时有: E(G=E(C)= +1 这就证明了(2)。 注:推论的条件是充分而非必要的
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 (2) 对于C1,n,有: 除此之外,只有当m=2且n=5时有: 1 , 1 ( ) ( ) 1. 2 n n EG EC 这就证明了(2)。 , 1 ( ) ( ) 1. 2 m n n EG EC 注:推论的条件是充分而非必要的

例如,在下图中,尽管C2.十v的边数不满足推 论不等式,可它是H图。 C2.7tuv 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 例如,在下图中,尽管C2,7+uv的边数不满足推 论不等式,可它是H图。 u v C2,7+uv

例1设G是度序列为(d1,d2,dn)的非平凡单图,且 d1≤d2≤.≤dn。证明:若G不存在小于(m+1)/2的正 整数m,使得:dm<m且dn-m+1<n-m,则G有H路。 证明:在G之外加上一个新点¥,把它和G的其余各 点连接得图G1 G G,的度序列为:(d1+1,d2+1,…,dn+1,n) 由条件:不存在小于(n+1)/2的正整数m,使得 dm十1≤m,且dmm1+1<n-m+1=(n+1)-m。于是由度序列 判定定理知:G是H图,得G有H路
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 例1 设G是度序列为(d1,d2,…,dn)的非平凡单图,且 d1≦d2≦…≦dn。证明:若G不存在小于(n+1)/2的正 整数m,使得:dm<m且dn-m+1<n-m,则G有H路。 证明:在G之外加上一个新点v,把它和G的其余各 点连接得图G1 G G1 v G1的度序列为: (d1+1,d2+1,…,dn+1, n) 由条件:不存在小于(n+1)/2的正整数m,使得 dm+1≦m,且dn-m+1+1<n-m+1=(n+1)-m。于是由度序列 判定定理知:G1是H图,得G有H路