
本次课主要内容 特殊平面图与平面图的对偶图 (一)、特殊平面图 1、极大平面图及其性质 2、极大外平面图及其性质 (二)、平面图的对偶图
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (一)、特殊平面图 (二)、平面图的对偶图 特殊平面图与平面图的对偶图 1、极大平面图及其性质 2、极大外平面图及其性质

(一)、特殊平面图 1、极大平面图及其性质 对于一个简单平面图来说,在不邻接顶点对间加边, 当边数增加到一定数量时,就会变成非平面图。这样, 就启发我们研究平面图的极图问题。 定义1设G是简单可平面图,如果G是K(1≤i≤4),或 者在G的任意非邻接顶点间添加一条边后,得到的图均是 非可平面图,则称G是极大可平面图。 极大可平面图的平面嵌入称为极大平面图
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 1、极大平面图及其性质 (一)、特殊平面图 对于一个简单平面图来说,在不邻接顶点对间加边, 当边数增加到一定数量时,就会变成非平面图。这样, 就启发我们研究平面图的极图问题。 定义1 设G是简单可平面图,如果G是Ki (1≦i≦4),或 者在G的任意非邻接顶点间添加一条边后,得到的图均是 非可平面图,则称G是极大可平面图。 极大可平面图的平面嵌入称为极大平面图
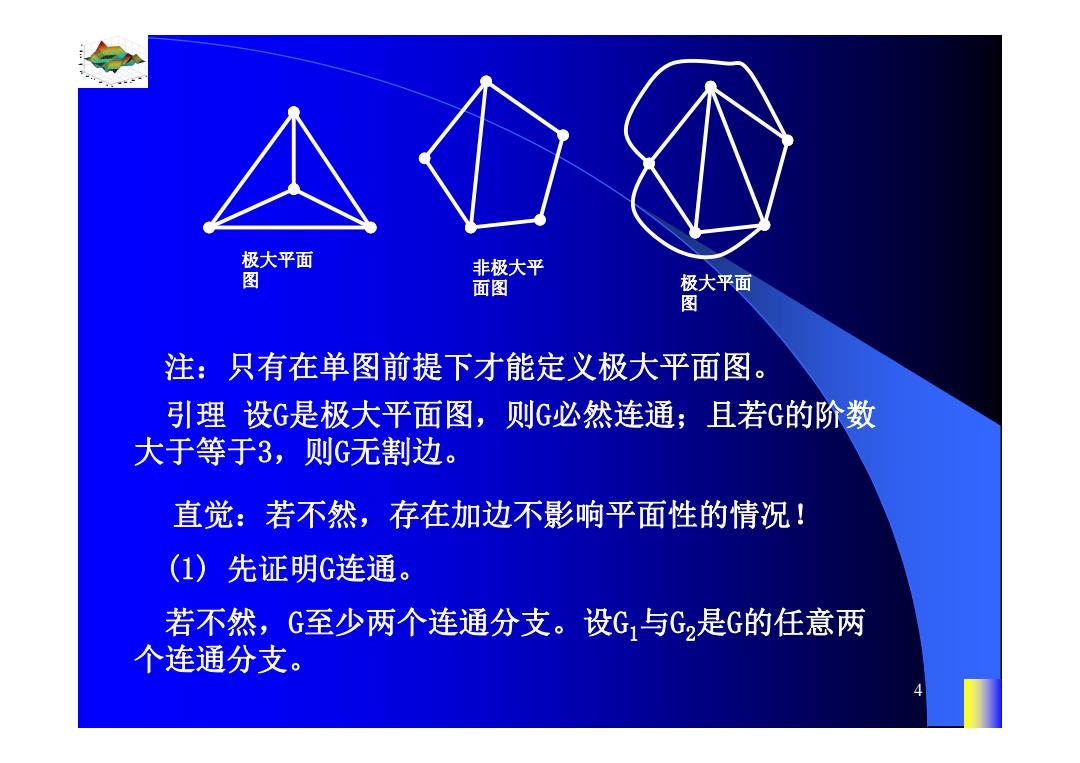
极大平面 非极大平 面图 极大平面 图 注:只有在单图前提下才能定义极大平面图。 引理设G是极大平面图,则G必然连通;且若G的阶数 大于等于3,则G无边。 直觉:若不然,存在加边不影响平面性的情况! (1)先证明G连通。 若不然,G至少两个连通分支。设G与G2是G的任意两 个连通分支
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 注:只有在单图前提下才能定义极大平面图。 引理 设G是极大平面图,则G必然连通;且若G的阶数 大于等于3,则G无割边。 极大平面 图 非极大平 面图 极大平面 图 (1) 先证明G连通。 若不然,G至少两个连通分支。设G1与G2是G的任意两 个连通分支。 直觉:若不然,存在加边不影响平面性的情况!
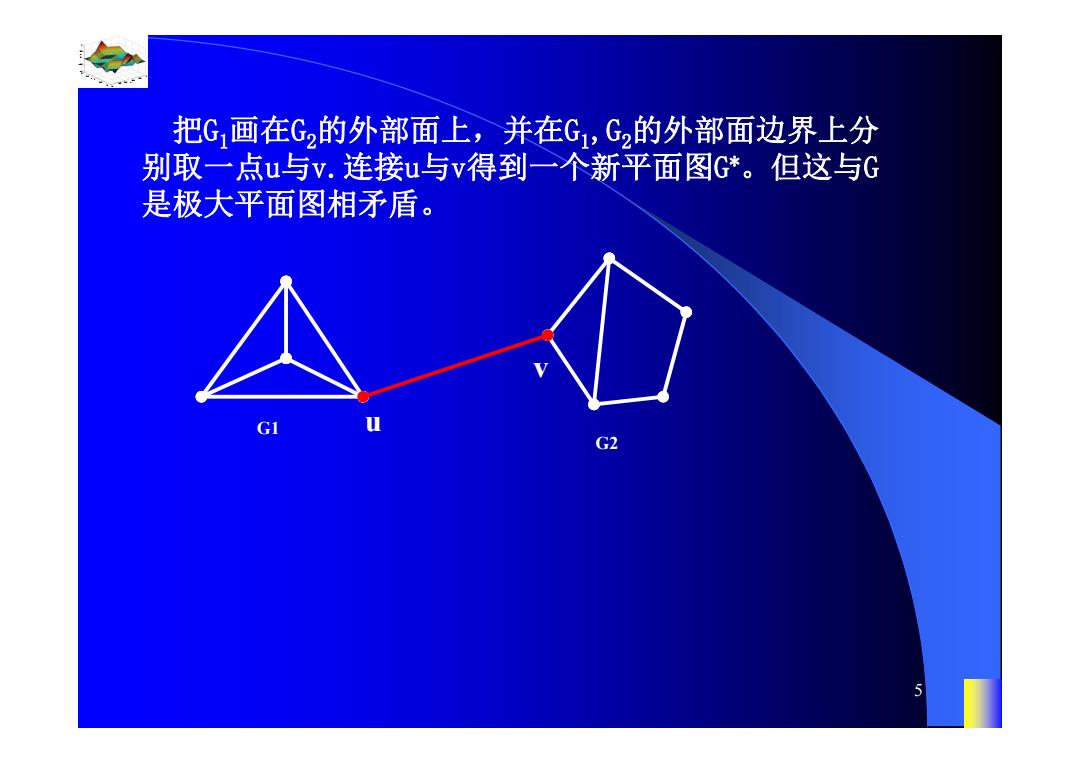
把G,画在G2的外部面上,并在G1,G2的外部面边界上分 别取一点u与v.连接u与v得到一个新平面图G*。但这与G 是极大平面图相矛盾。 G1 G2
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 把G1画在G2的外部面上,并在G1,G2的外部面边界上分 别取一点u与v.连接u与v得到一个新平面图G*。但这与G 是极大平面图相矛盾。 G1 G2 v u
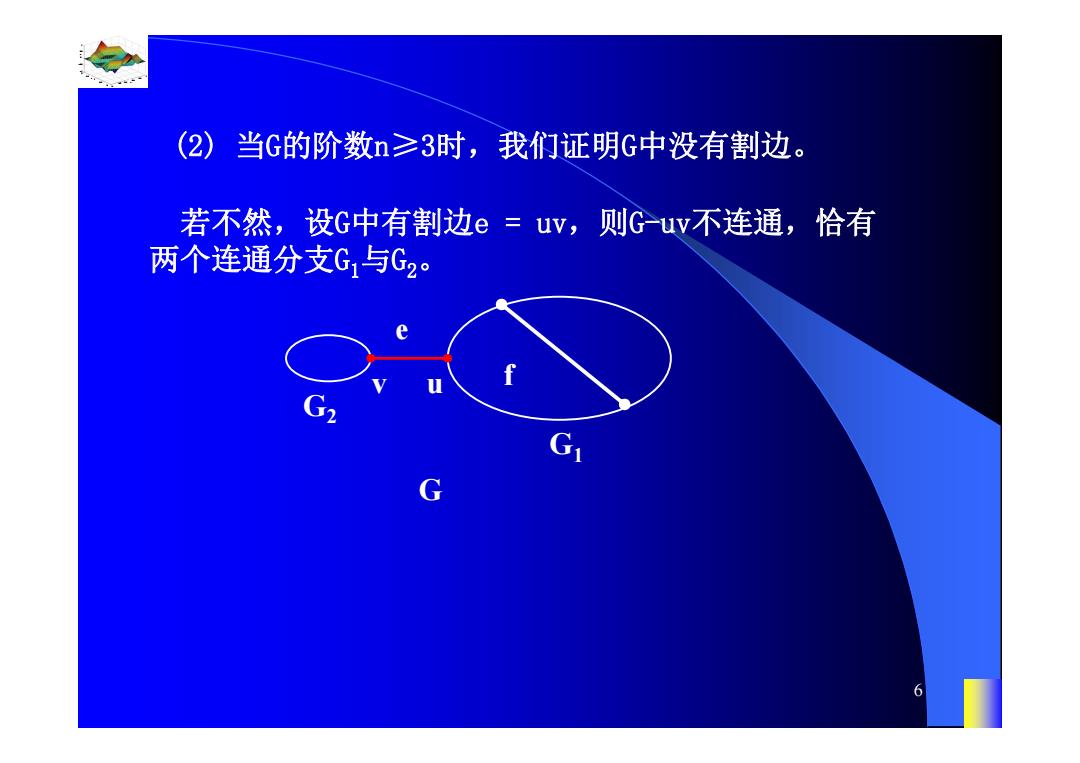
(2)当G的阶数n≥3时, 我们证明G中没有割边。 若不然,设G中有割边e=uv,则Guv不连通,恰有 两个连通分支G1与G2。 G 6
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 (2) 当G的阶数n≥3时,我们证明G中没有割边。 若不然,设G中有割边e = uv,则G-uv不连通,恰有 两个连通分支G1与G2。 v u e G1 G2 G f
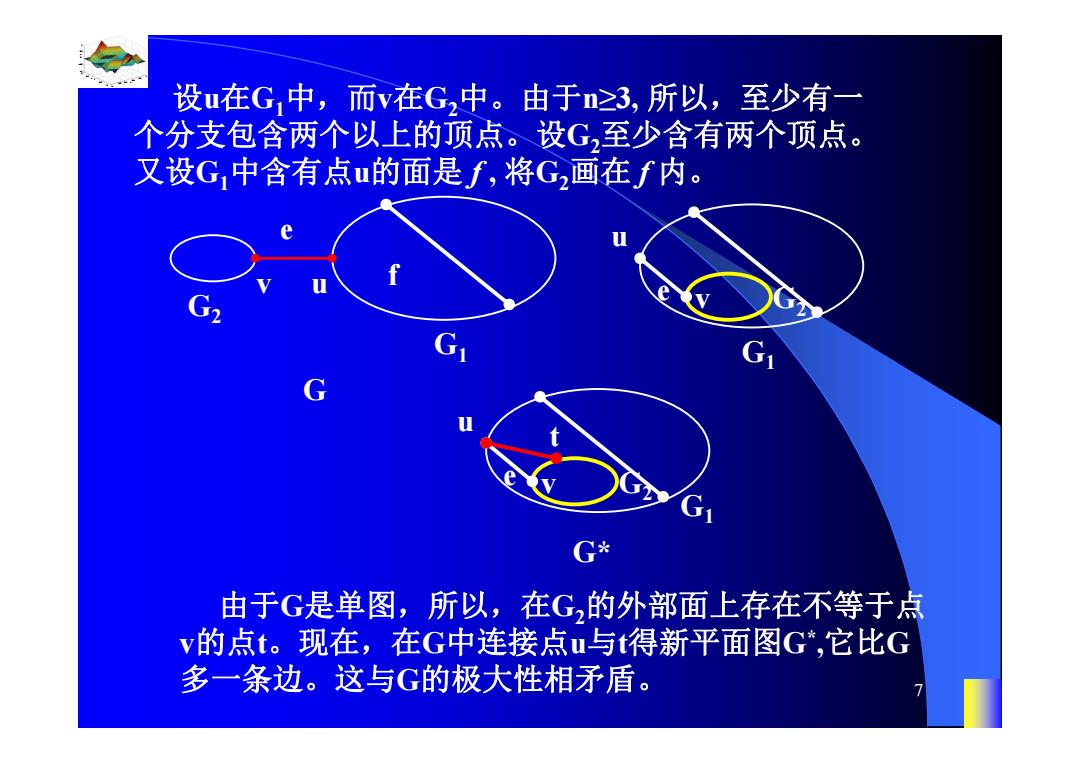
设u在G,中,而v在G2中。由于n≥3,所以,至少有一 个分支包含两个以上的顶点。设G,至少含有两个顶点。 又设G,中含有点u的面是f,将G2画在f内。 G* 由于G是单图,所以,在G,的外部面上存在不等于点 v的点t。现在,在G中连接点u与t得新平面图G*,它比G 多一条边。这与G的极大性相矛盾
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 设u在G1中,而v在G2中。由于n≥3, 所以,至少有一 个分支包含两个以上的顶点。设G2至少含有两个顶点。 又设G1中含有点u的面是 f , 将G2画在 f 内。 由于G是单图,所以,在G2的外部面上存在不等于点 v的点t。现在,在G中连接点u与t得新平面图G*,它比G 多一条边。这与G的极大性相矛盾。 v u e G1 G2 v u e G1 G2 G f v u e G1 G2 t G*
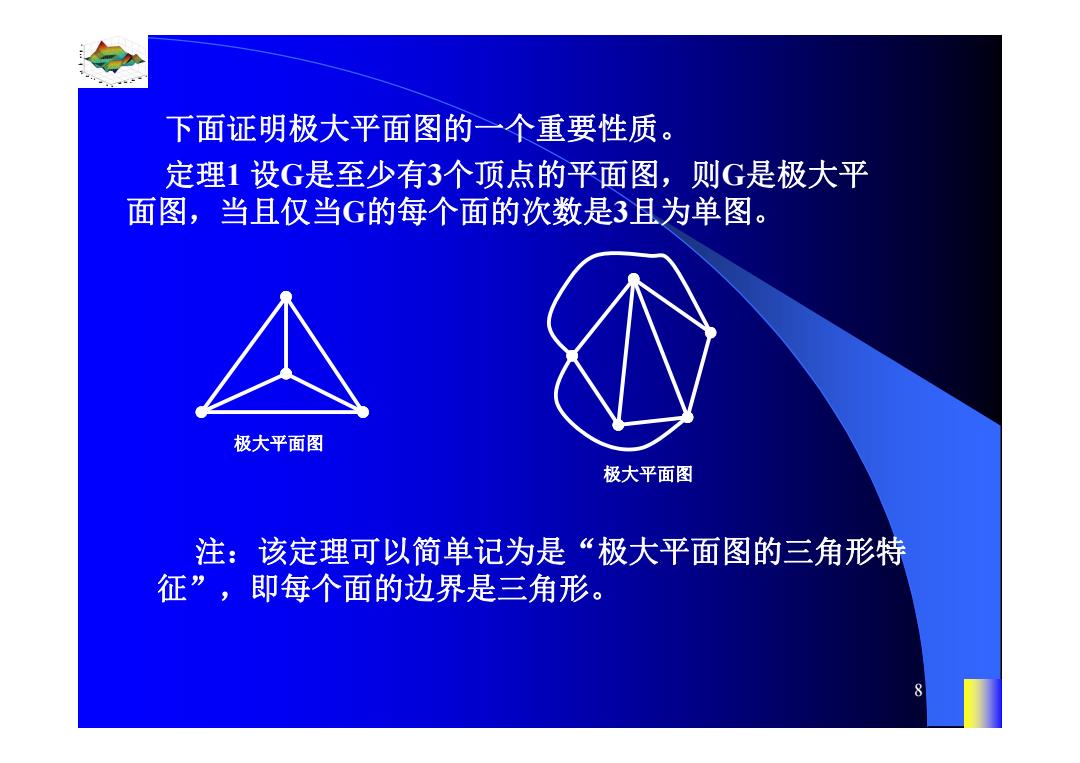
下面证明极大平面图的一个重要性质。 定理1设G是至少有3个顶点的平面图,则G是极大平 面图,当且仅当G的每个面的次数是3且为单图。 极大平面图 极大平面图 注:该定理可以简单记为是“极大平面图的三角形特 征”,即每个面的边界是三角形
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 下面证明极大平面图的一个重要性质。 定理1 设G是至少有3个顶点的平面图,则G是极大平 面图,当且仅当G的每个面的次数是3且为单图。 注:该定理可以简单记为是“极大平面图的三角形特 征”,即每个面的边界是三角形。 极大平面图 极大平面图
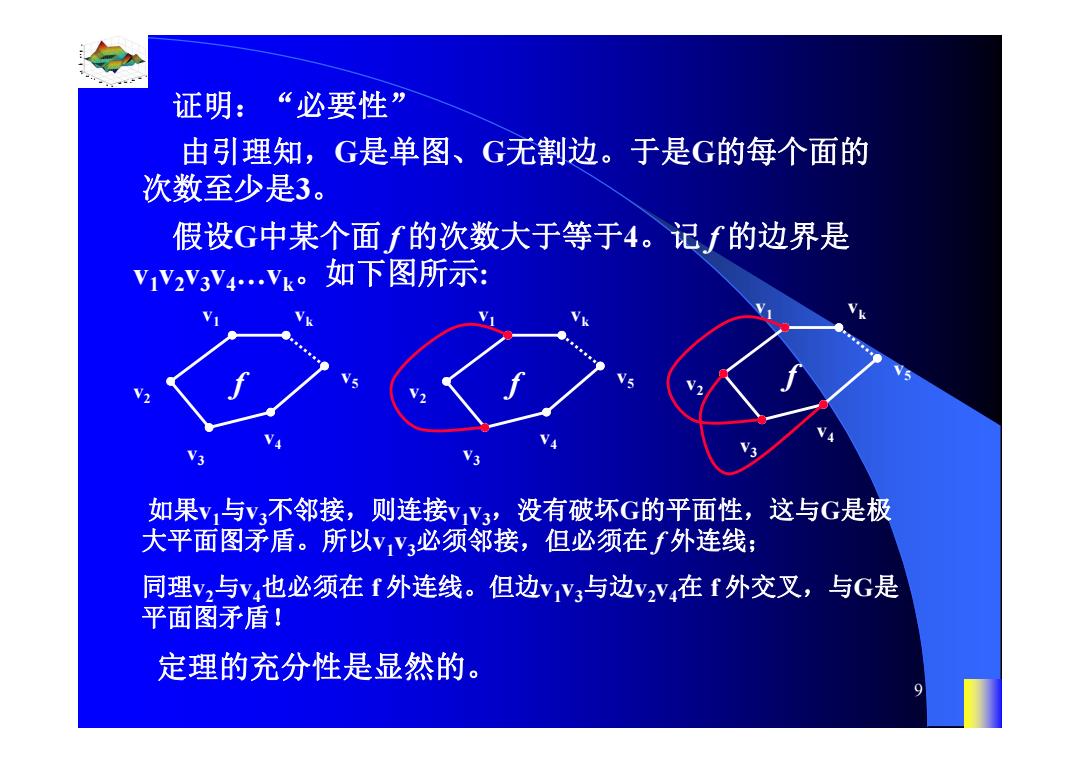
证明:“必要性 由引理知,G是单图、 G无割边。于是G的每个面的 次数至少是3。 假设G中某个面f的次数大于等于4。记f的边界是 VV2Y3V4Vk。如下图所示: 如果v,与v3不邻接,则连接vV3,没有破坏G的平面性,这与G是极 大平面图矛盾。所以vY3必须邻接,但必须在f外连线; 同理v2与v也必须在f外连线。但边yV3与边v2Y在f外交叉,与G是 平面图矛盾! 定理的充分性是显然的
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 证明:“必要性” 由引理知,G是单图、G无割边。于是G的每个面的 次数至少是3。 假设G中某个面 f 的次数大于等于4。记 f 的边界是 v1v2v3v4…vk。如下图所示: v1 v2 v3 v4 v5 vk f 如果v1与v3不邻接,则连接v1v3,没有破坏G的平面性,这与G是极 大平面图矛盾。所以v1v3必须邻接,但必须在 f 外连线; 定理的充分性是显然的。 v1 v2 v3 v4 v5 vk f v1 v2 v3 v4 v5 vk f 同理v2与v4也必须在 f 外连线。但边v1v3与边v2v4在 f 外交叉,与G是 平面图矛盾!

推论:设G是n个点,m条边和中个面的极大平面图, 且n≥3.则:(1)m=3n-6;(2) Φ=2n-4. 证明:因为G是极大平面图,所以,每个面的次数为3. 由次数公式: 21m= ∑deg(f)=3 由欧拉公式: 0=2-n+m 所以得: 2 m=2-1n+n 3 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 推论:设G是n个点,m条边和ф个面的极大平面图, 且n≥3.则:(1) m=3n-6; (2) ф=2n-4. 证明:因为G是极大平面图,所以,每个面的次数为3. 由次数公式: 2 deg( ) 3 f m f 由欧拉公式: 2 n m 所以得: 2 2 3 m nm
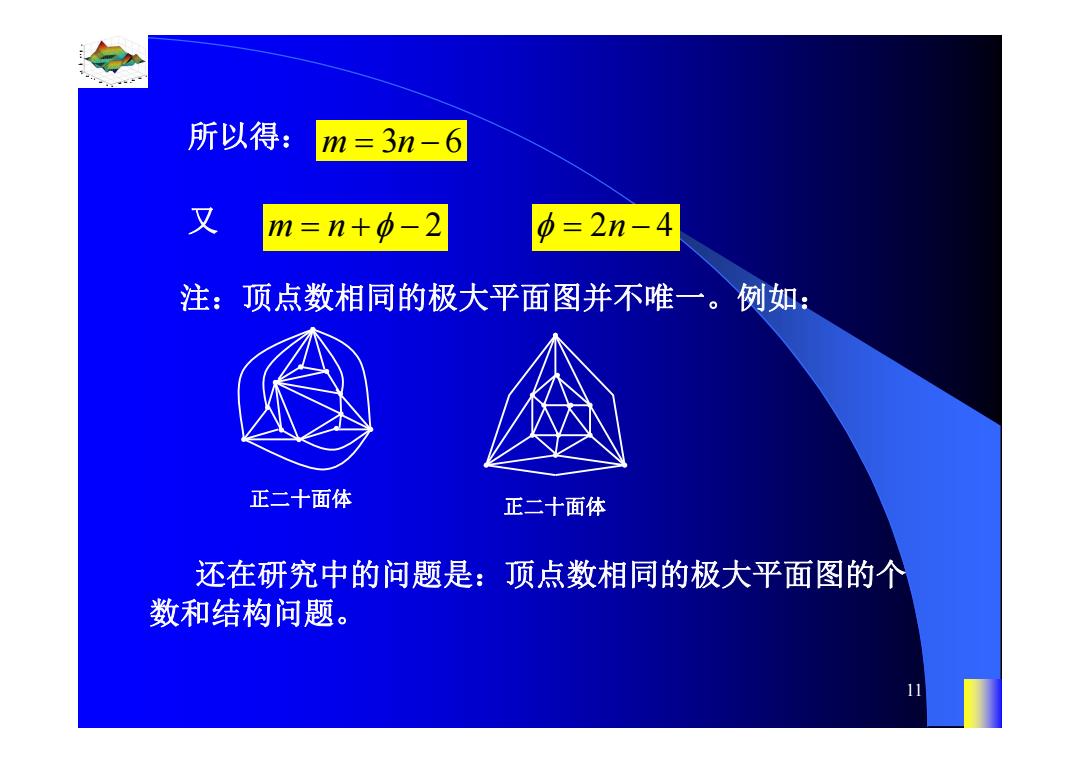
所以得: m=3n-6 又 m=n+-2 =2n-4 注:顶点数相同的极大平面图并不唯一。例如: 正二十面体 正二十面体 还在研究中的问题是:顶点数相同的极大平面图的个 数和结构问题
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 所以得: m n 3 6 又 m n 2 2 4 n 注:顶点数相同的极大平面图并不唯一。例如: 正二十面体 正二十面体 还在研究中的问题是:顶点数相同的极大平面图的个 数和结构问题