
本次课主要内容 偶图的匹配问题 (一)、: 图的匹配与贝尔热定理 (二)、偶图的匹配与覆盖
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 本次课主要内容 (一)、图的匹配与贝尔热定理 (二)、偶图的匹配与覆盖 偶图的匹配问题

关于偶图的基础回顾 1、定义:所谓具有二分类(X,Y的偶图(或二部图)是 指一个图,它的点集可以分解为两个(非空)子集X和Y,使得 每条边的一个端点在X中,另一个端点在中. 注:1、偶图不能有环,偶图可以有重边; 2、偶图刻画的是两类事物之间的某种联系状态
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 关于偶图的基础回顾 1、定义:所谓具有二分类(X, Y)的偶图(或二部图)是 指一个图,它的点集可以分解为两个(非空)子集X和Y,使得 每条边的一个端点在X中,另一个端点在Y中. A G B C D E F a b c d efg 注:1、偶图不能有环,偶图可以有重边; 2、偶图刻画的是两类事物之间的某种联系状态

2、k-正则偶图 每个顶点度数均为k的偶图称为k-正则偶图。 2-正则偶图 性质:k-正则偶图的两个顶点子集包含顶点个数相等 3、图G是偶图当且仅当G不含奇圈【判定定理】
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 2、k-正则偶图 每个顶点度数均为k的偶图称为k-正则偶图。 2-正则偶图 性质:k-正则偶图的两个顶点子集包含顶点个数相等。 3、图G是偶图当且仅当G不含奇圈【判定定理】
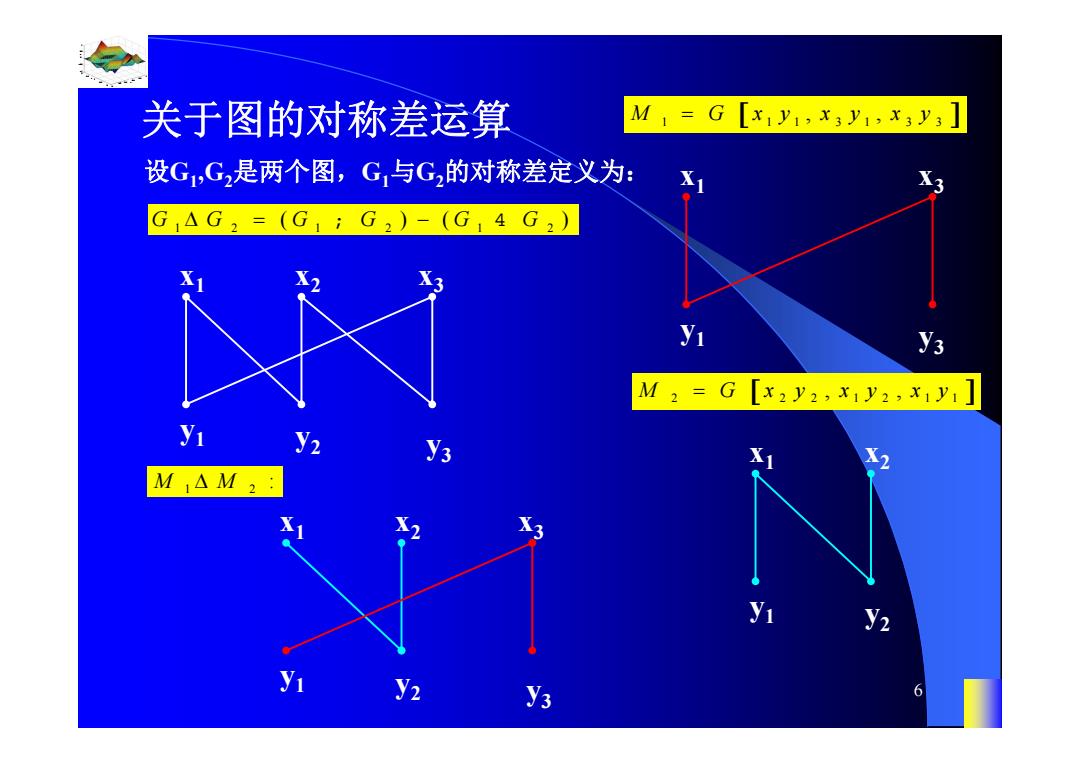
关于图的对称差运算 M1=G[x1y1,x3y1,x;y3] 设G1,G,是两个图,G,与G的对称差定义为: G,△G2=(G1;G2)-(G14G2) M2=G[x2y2,x1y2,x1y1] Y1 y2 Y3 M1△M2: y2 y y2 Ve 6
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 关于图的对称差运算 设G1,G2是两个图,G1与G2的对称差定义为: 12 1 2 1 2 GG G G G G ( )( ) U I y3 y2 y1 x1 x2 x3 M 1 11 31 3 3 G xy xy xy , , M 2 2 2 1 2 11 G x y xy xy , , y1 x1 x3 y3 y2 y1 x1 x2 y3 y2 y1 x1 x2 x3 1 2 M M :

(一)、 图的匹配与贝尔热定理 1、图的匹配相关概念 (1)、匹配M-如果M是图G的边子集(不含环),且 M中的任意两条边没有共同顶点,则称M是G的一个匹 配或对集或边独立集。 如果G中顶点v是G的匹配M中某条边的端点,称它 为M饱和点,否则为M非饱和点。 M={vov-} M=VoV7,VIVs} M3={VGV7,VIVs,V3V4} M1,M2,M3等都是G的匹配
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 1、图的匹配相关概念 (1)、匹配 M--- 如果M是图G的边子集(不含环),且 M中的任意两条边没有共同顶点,则称M是G的一个匹 配或对集或边独立集。 (一)、图的匹配与贝尔热定理 如果G中顶点v是G的匹配 M中某条边的端点,称它 为M饱和点,否则为M非饱和点。 v1 v7 v6 G v8 v2 v3 v5 v4 M1={v6v7} M2={v6v7, v1v8} M3={v6v7, v1v8, v3v4} M1,M2,M3等都是G的匹配
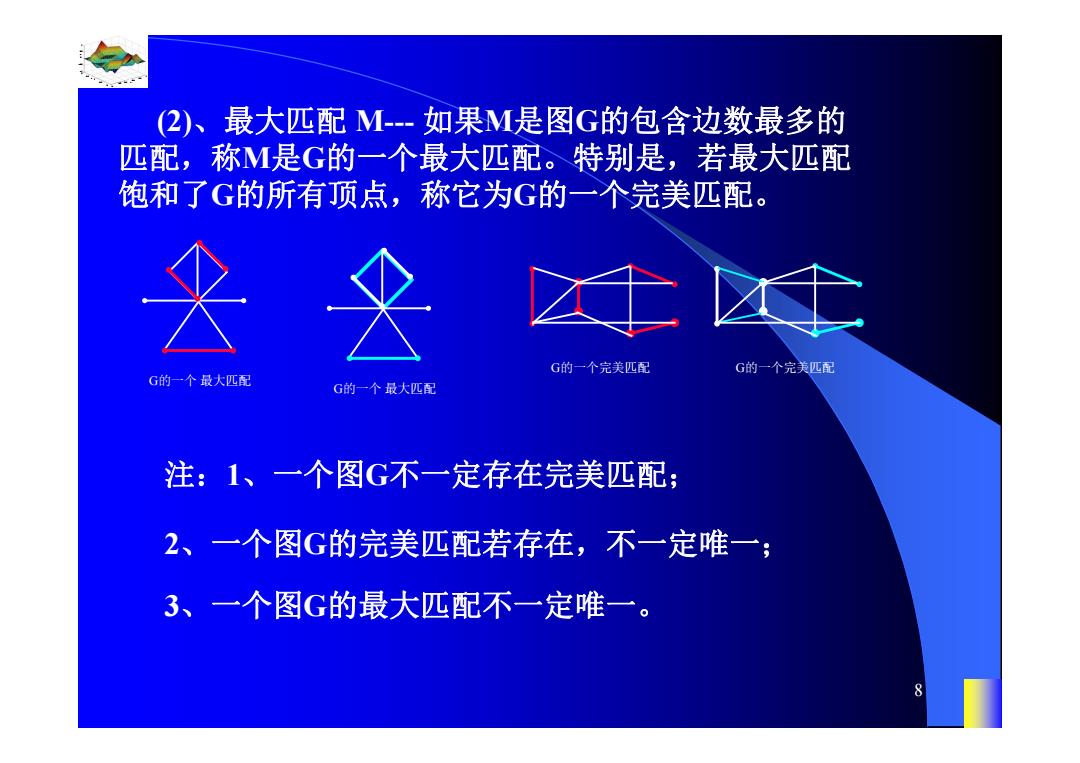
(2)、最大匹配M--如果M是图G的包含边数最多的 匹配,称M是G的一个最大匹配。特别是,若最大匹配 饱和了G的所有顶点,称它为G的一个完美匹配。 G的一个完美匹配 G的一个完美匹配 G的一个最大匹配 G的一个最大匹配 注:1、一个图G不一定存在完美匹配; 2、一个图G的完美匹配若存在,不一定唯一; 3、一个图G的最大匹配不一定唯一。 8
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 (2)、最大匹配 M--- 如果M是图G的包含边数最多的 匹配,称M是G的一个最大匹配。特别是,若最大匹配 饱和了G的所有顶点,称它为G的一个完美匹配。 G的一个 最大匹配 G的一个完美匹配 注:1、一个图G不一定存在完美匹配; G的一个 最大匹配 G的一个完美匹配 2、一个图G的完美匹配若存在,不一定唯一; 3、一个图G的最大匹配不一定唯一

(③)、M交错路- 如果M是图G的匹配,G中一条由M 中的边和非M中的边交错形成的路,称为G中的一条M 交错路。特别地,若M交错路的起点与终点是M非饱和 点,称这种M交错路为M可扩路。 在下图中: 设M=(vV8,V3Y4},则: 路VGV-VsV3Y与IV-V8V2都是M交错路。其中后者是M 可扩路。 注意:M=(vYg)M=(vY4等,也叫M交错路
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 (3)、M交错路--- 如果M是图G的匹配,G中一条由M 中的边和非M中的边交错形成的路,称为G中的一条M 交错路。特别地,若M交错路的起点与终点是M非饱和 点,称这种M交错路为M可扩路。 在下图中: v1 v7 v6 G v8 v2 v3 v5 v4 设M={v7v8 , v3v4},则: 路v6v7v8v3v4与v1v7v8v2都是M交错路。其中后者是M 可扩路。 注意:M ={v7v8 } M ={v3v4 }等,也叫M交错路

2、贝尔热定理 定理1(贝尔热,1957G的匹配M是最大匹配,当且 仅当G不包含M可扩路。 证明:“必要性” 若G包含一条M可扩路P,则可令该可扩路为: P VOVIV26 V2kV2k+1 V2k-1 2k+1 显然,P中M中的边比非M中的边少一条。于是作新的匹配 M,它当中的边由P中非M中边组成。M,中边比M中多一条, 这与M是G的最大匹配矛盾。 V2k-1 V2k+1 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 2、贝尔热定理 定理1 (贝尔热,1957) G的匹配M是最大匹配,当且 仅当G不包含M可扩路。 证明:“必要性” 若G包含一条M可扩路P,则可令该可扩路为: P 012 2 2 1 k k v vv v v L 显然,P中M中的边比非M中的边少一条。于是作新的匹配 M1,它当中的边由P中非M中边组成。M1中边比M中多一条, 这与M是G的最大匹配矛盾。 v0 v1 v2 v v2k-1 3 v4 v2k v2k+1 v0 v1 v2 v v2k-1 3 v4 v2k v2k+1
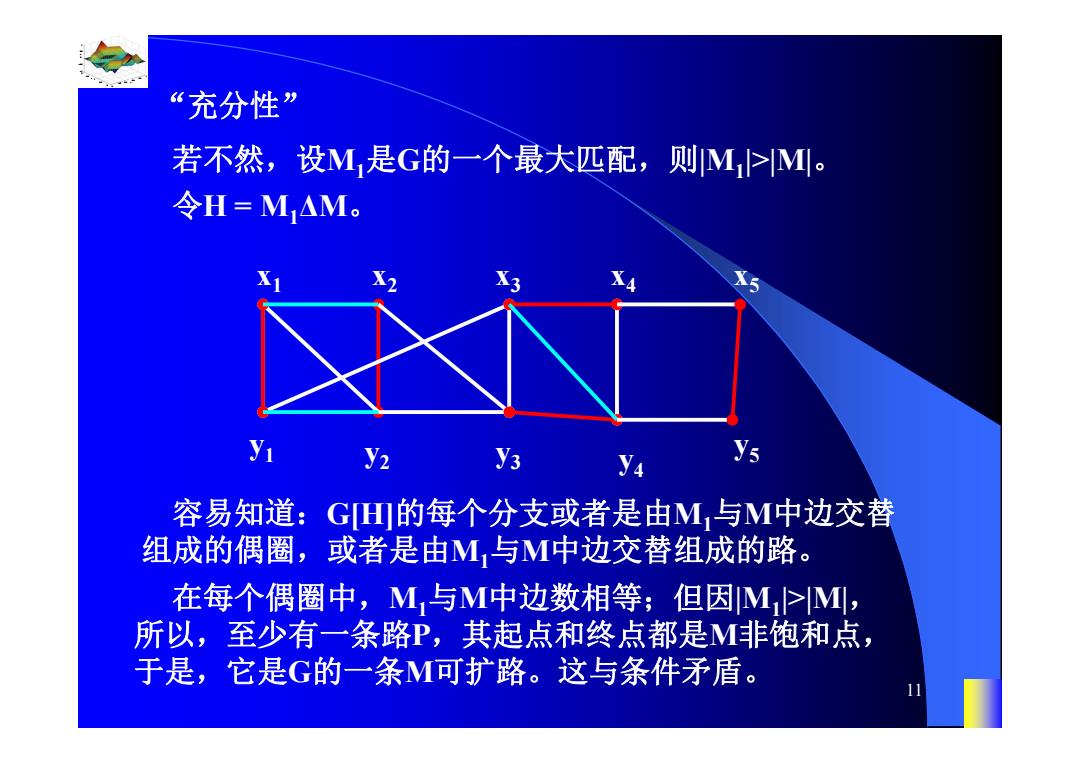
“充分性” 若不然,设M,是G的一个最大匹配,则M1>M。 令H=M△M。 Y1 Y2 Y3 Ya ys 容易知道:G山的每个分支或者是由M,与M中边交替 组成的偶圈,或者是由M与M中边交替组成的路。 在每个偶圈中,M,与M中边数相等;但因M>M, 所以,至少有一条路P,其起点和终点都是M非饱和点, 于是,它是G的一条M可扩路。这与条件矛盾
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 “充分性” 若不然,设M1是G的一个最大匹配,则|M1|>|M|。 令H = M1ΔM。 y2 y3 y1 x1 x2 x3 x4 y4 x5 y5 容易知道:G[H]的每个分支或者是由M1与M中边交替 组成的偶圈,或者是由M1与M中边交替组成的路。 在每个偶圈中,M1与M中边数相等;但因|M1|>|M|, 所以,至少有一条路P,其起点和终点都是M非饱和点, 于是,它是G的一条M可扩路。这与条件矛盾

注:贝尔热定理给我们提供了扩充G的匹配的思路。 贝尔热(1926--2002)法国著名数学家。他的《无限图 理论及其应用》(1958)是继哥尼之后的图论历史上的第 二本图论专著。他不仅在图论领域做出了许多贡献,而 且四处奔波传播图论,推动了图论的普及和发展。 1993年,他获得组合与图论领域颁发的欧拉奖章。 贝尔热在博弈论、拓扑学领域里也有杰出贡献。在 博弈领域,他引入了Nash均衡之外的另一种均衡系统。 Nash的生活被改编成电影《美丽的心灵》,获02年奥 斯卡金像奖。 贝尔热对中国的手工艺很感兴趣。他也是一位象棋 高手,还创作过小说《谁杀害了Densmore公爵》
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 12 注:贝尔热定理给我们提供了扩充G的匹配的思路。 贝尔热(1926---2002) 法国著名数学家。他的《无限图 理论及其应用》(1958) 是继哥尼之后的图论历史上的第 二本图论专著。他不仅在图论领域做出了许多贡献,而 且四处奔波传播图论,推动了图论的普及和发展。 1993年,他获得组合与图论领域颁发的欧拉奖章。 贝尔热在博弈论、拓扑学领域里也有杰出贡献。在 博弈领域,他引入了Nash均衡之外的另一种均衡系统。 Nash的生活被改编成电影《美丽的心灵》,获02年奥 斯卡金像奖。 贝尔热对中国的手工艺很感兴趣。他也是一位象棋 高手,还创作过小说《谁杀害了Densmore公爵》