
本次课主要内容 哈密尔顿图 (一)、哈密尔顿图的概念 (二)、性质与判定
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (一)、哈密尔顿图的概念 (二)、性质与判定 哈密尔顿图

(一)、哈密尔顿图的概念 1、背景 l857年,哈密尔顿发明了一个游戏cosian Game), 它是由一个木制的正十二面体构成,在它的每个棱角 处标有当时很有名的城市。游戏目的是“环球旅行 ” 为了容易记住被旅游过的城市,在每个棱角上放上 个钉子,再用一根线绕在那些旅游过的城市上(钉子) 由此可以获得旅程的直观表示。 十二面体
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 1、背景 (一)、哈密尔顿图的概念 1857年, 哈密尔顿发明了一个游戏(Icosian Game). 它是由一个木制的正十二面体构成,在它的每个棱角 处标有当时很有名的城市。游戏目的是“环球旅行”。 为了容易记住被旅游过的城市 ,在每个棱角上放上一 个钉子,再用一根线绕在那些旅游过的城市上(钉子), 由此可以获得旅程的直观表示。 十二面体

哈密尔顿把该游戏以25英镑的价格买给了J.Jacques and Sons公司(该公司如今以制造国际象棋设备而著 名),1859年获得专利权。但商业运作失败了。 该游戏促使人们思考点线连接的图的结构特征。这 就是图论历史上著名的哈密尔顿问题。 哈密尔顿(1805--1865,爱尔兰数学家。个人生活很 不幸,但兴趣广泛:诗歌、光学、天文学和数学无所 不能。他的主要贡献是在代数领域,发现了四元数(第 一个非交换代数),他认为数学是最美丽的花朵。 2、哈密尔顿图与哈密尔顿路 定义1如果经过图G的每个顶点恰好一次后能够回到 出发点,称这样的图为哈密尔顿图,简称H图。所经过 的闭途径是G的一个生成圈,称为G的哈密尔顿圈
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 哈密尔顿(1805---1865),爱尔兰数学家。个人生活很 不幸,但兴趣广泛:诗歌、光学、天文学和数学无所 不能。他的主要贡献是在代数领域,发现了四元数(第 一个非交换代数),他认为数学是最美丽的花朵。 哈密尔顿把该游戏以25英镑的价格买给了J.Jacques and Sons公司 (该公司如今以制造国际象棋设备而著 名) ,1859年获得专利权。但商业运作失败了。 该游戏促使人们思考点线连接的图的结构特征。这 就是图论历史上著名的哈密尔顿问题。 2、哈密尔顿图与哈密尔顿路 定义1 如果经过图G的每个顶点恰好一次后能够回到 出发点,称这样的图为哈密尔顿图,简称H图。所经过 的闭途径是G的一个生成圈,称为G的哈密尔顿圈
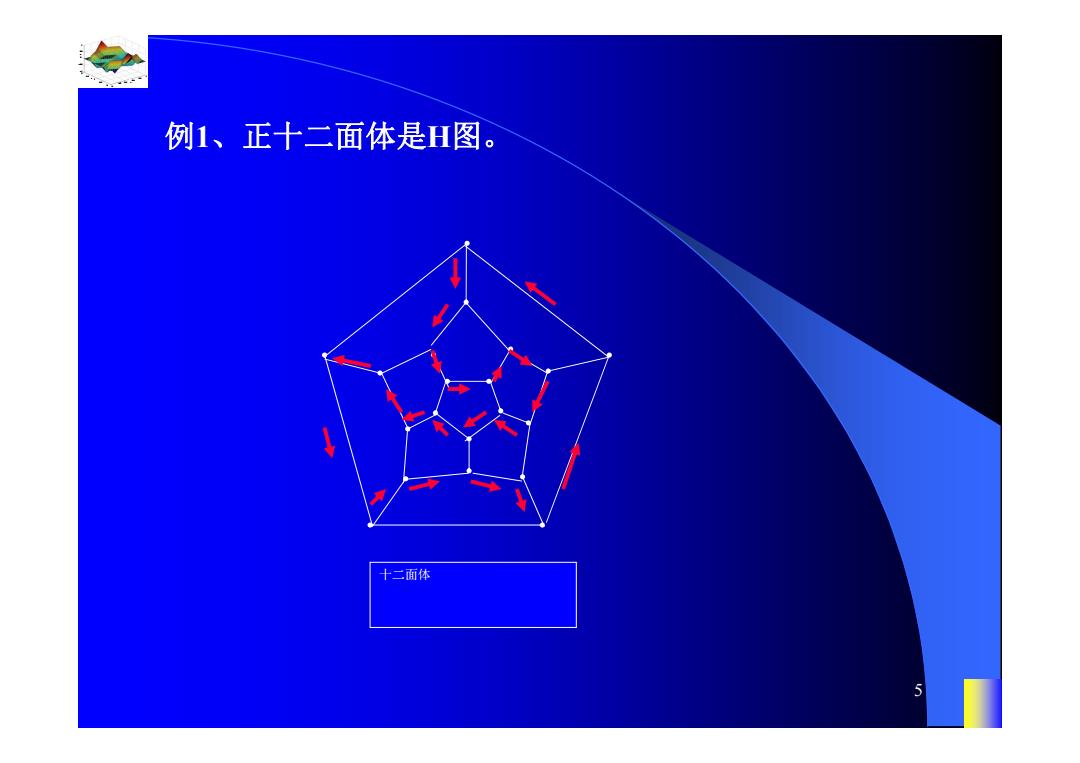
例1、正十二面体是H图。 十二面体
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 例1、正十二面体是H图。 十二面体
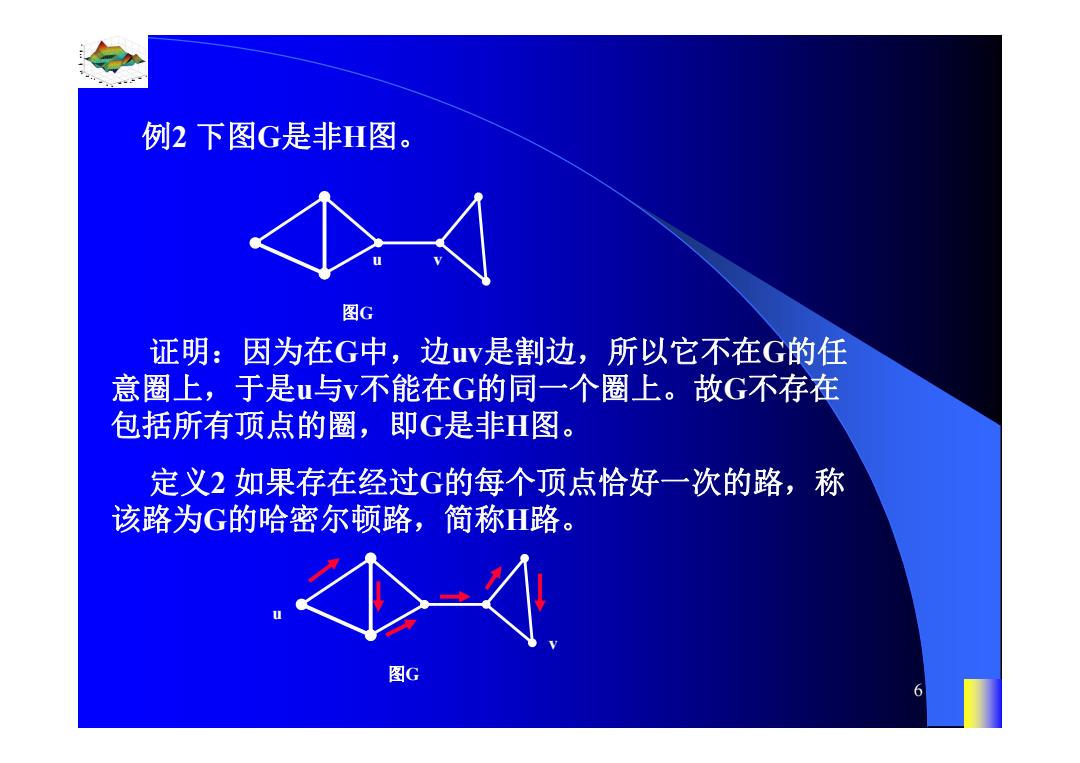
例2下图G是非H图。 图G 证明:因为在G中,边v是割边,所以它不在G的任 意圈上,于是u与v不能在G的同一个圈上。故G不存在 包括所有顶点的圈,即G是非H图。 定义2如果存在经过G的每个顶点恰好一次的路,称 该路为G的哈密尔顿路,简称H路。 图G
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 例2 下图G是非H图。 证明:因为在G中,边uv是割边,所以它不在G的任 意圈上,于是u与v不能在G的同一个圈上。故G不存在 包括所有顶点的圈,即G是非H图。 图G u v 定义2 如果存在经过G的每个顶点恰好一次的路,称 该路为G的哈密尔顿路,简称H路。 u v 图G

(二)、性质与判定 1、性质 定理1(必要条件)若G为H图,则对V(G)的任一非空 顶点子集S,有: o(G-S)≤lS 证明:G是H图,设C是G的H圈。则对V(G)的任意 非空子集S,容易知道: o(C-S)≤lS到 所以,有: o(G-S)≤o(C-S)≤S
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 (二)、性质与判定 1、性质 定理1 (必要条件) 若G为H图,则对V(G)的任一非空 顶点子集S,有: ( ) GS S 证明:G是H图,设C是G的H圈。则对V(G)的任意 非空子集S, 容易知道: ( ) CS S 所以,有: ( )( ) GS CS S

注:不等式为G是H图的必要条件,即不等式不满足 时,可断定对应图是非H图。 例3求证下图是非H图。 G 证明:取S={2,7,6},则有:o(G-S)=4>S=3 所以由定理1知,G为非H图。 8
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 注:不等式为G是H图的必要条件,即不等式不满足 时,可断定对应图是非H图。 例3 求证下图是非H图。 证明:取S={2, 7, 6},则有: 4 5 3 2 1 8 7 6 9 ( )4 3 GS S 所以由定理1知,G为非H图。 G

注意:满足定理1不等式的图不一定是H图。 例如:著名的彼德森图是非H图,但它满足定理1的 不等式。 Peterson图 彼得森(1839--1910),丹麦哥本哈根大学数学教授。 家境贫寒,因此而辍过学。但19岁就出版了关于对数的 专著。他作过中学教师,32岁获哥本哈根大学数学博士 学位,然后一直在该大学作数学教授
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 注意:满足定理1不等式的图不一定是H图。 例如:著名的彼德森图是非H图,但它满足定理1的 不等式。 Peterson图 彼得森(1839----1910),丹麦哥本哈根大学数学教授。 家境贫寒,因此而辍过学。但19岁就出版了关于对数的 专著。他作过中学教师,32岁获哥本哈根大学数学博士 学位,然后一直在该大学作数学教授

彼得森是一位出色的名教师。他讲课遇到推理困难时, 总是说:“这是显而易见的”,并让学生自己查阅他的著 作。同时,他是一位有经验的作家,论述问题很形象,讲 究形式的优雅。 1891年,彼得森发表了一篇奠定他图论历史地位的长达 28页的论文。这篇文章被公认是第一篇包含图论基本结论 的文章。同时也是第一次在文章中使用“图”术语。 1898年,彼得森又发表了一篇只有3页的论文,在这篇文 章中,为举反例构造了著名的彼得森图。 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 彼得森是一位出色的名教师。他讲课遇到推理困难时, 总是说:“这是显而易见的”,并让学生自己查阅他的著 作。同时,他是一位有经验的作家,论述问题很形象,讲 究形式的优雅。 1891年,彼得森发表了一篇奠定他图论历史地位的长达 28页的论文。这篇文章被公认是第一篇包含图论基本结论 的文章。同时也是第一次在文章中使用“图”术语。 1898年,彼得森又发表了一篇只有3页的论文,在这篇文 章中,为举反例构造了著名的彼得森图

2、判定 图的H性判定是NP困难问题。到目前为止,有关的 定理有300多个,但没有一个是理想的。拓展H图的实 用特征仍然被图论领域认为是重大而没有解决的问题。 图的哈密尔顿问题和四色问题被谓为挑战图论领域 150年智力极限的总和。三位数学“诺奖”获得者 ErdOs、Whitney、Lovasz以及Dirac、Ore等在哈密 尔顿问题上有过杰出贡献。 下面,介绍几个著名的定理
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 2、判定 图的H性判定是NP-困难问题。到目前为止,有关的 定理有300多个,但没有一个是理想的。拓展H图的实 用特征仍然被图论领域认为是重大而没有解决的问题。 图的哈密尔顿问题和四色问题被谓为挑战图论领域 150年智力极限的总和。三位数学“诺奖”获得者 ErdÖs、Whitney 、 Lovász 以及Dirac、Ore等在哈密 尔顿问题上有过杰出贡献。 下面,介绍几个著名的定理