
本次课主要内容 (一)、生成树的概念与性质 (二)、生成树的计数 (三)、回路系统简介
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (一)、生成树的概念与性质 (二)、生成树的计数 (三)、回路系统简介

(一)、生成树的概念与性质 1、生成树的概念 定义1图G的一个生成子图T如果是树,称它为G的一棵 生成树;若T为森林,称它为G的一个生成森林。 生成树的边称为树枝,G中非生成树的边称为弦。 例如: 图G 粗边构成的子图为G的生成树
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 1、生成树的概念 (一)、生成树的概念与性质 定义1 图G的一个生成子图T如果是树,称它为G的一棵 生成树;若T为森林,称它为G的一个生成森林。 生成树的边称为树枝,G中非生成树的边称为弦。 例如: 粗边构成的子图为G的生成树。 图G

2、生成树的性质 定理1每个连通图至少包含一棵生成树 证明:如果连通图G是树,则其本身是一棵生成树; 若连通图G中有圈C,则去掉C中一条边后得到的图仍 然是连通的,这样不断去掉G中圈,最后得到一个G的 无圈连通子图T,它为G的一棵生成树。 定理1的证明实际上给出了连通图G的生成树的求法, 该方法称为破圈法。 利用破圈法,显然也可以求出任意图的一个生成森林
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 2、生成树的性质 定理1 每个连通图至少包含一棵生成树。 证明:如果连通图G是树,则其本身是一棵生成树; 若连通图G中有圈C,则去掉C中一条边后得到的图仍 然是连通的,这样不断去掉G中圈,最后得到一个G的 无圈连通子图T,它为G的一棵生成树。 定理1的证明实际上给出了连通图G的生成树的求法, 该方法称为破圈法。 利用破圈法,显然也可以求出任意图的一个生成森林

推论若G是(n,m)连通图,则m≥nl 连通图G的生成树一般不唯一! (二)、生成树的计数 1、凯莱递推计数法 凯莱(Cayley1821一1895):剑桥大学数学教授,著名 代数学家,发表论文数仅次于Erdos,Euler,,Cauchy.著 名成果是1854年定义了抽象群,并且得到著名定理:任 意一个群都和一个变换群同构。同时,他也是一名出色 的律师,作律师14年期间,发表200多篇数学论文,著 名定理也是在该期间发表的。 凯莱生成树递推计数公式是他在1889年建立的
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 推论 若G是(n, m)连通图,则m≧n-1 连通图G的生成树一般不唯一! (二)、生成树的计数 1、凯莱递推计数法 凯莱(Cayley 1821—1895): 剑桥大学数学教授,著名 代数学家,发表论文数仅次于Erdos ,Euler, Cauchy. 著 名成果是1854年定义了抽象群,并且得到著名定理:任 意一个群都和一个变换群同构。同时,他也是一名出色 的律师,作律师14年期间,发表200多篇数学论文,著 名定理也是在该期间发表的。 凯莱生成树递推计数公式是他在1889年建立的
定义2图G的边e称为被收缩,是指删掉e后,把e的两 个端点重合,如此得到的图记为G.e 用τ(G)表示G的生成树棵数。 定理2(Cayley)设e是G的一条边,则有: (G)=t(G-e)+t(G e) 证明:对于G的一条边e来说,G的生成树中包含边e的 棵数为t(G.e),而不包含e的棵数为r(G-e)
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 定义2 图G的边e称为被收缩,是指删掉e后,把e的两 个端点重合,如此得到的图记为G.e e1 e5 e2 e4 e3 用τ(G)表示G的生成树棵数。 定理2 (Cayley) 设e是G的一条边,则有: () ( ) ( ) G G e Ge 证明:对于G的一条边e来说,G的生成树中包含边e的 棵数为τ(G.e ),而不包含e的棵数为τ (G-e)

例1,利用凯莱递推法求下图生成树的棵数。 共8棵生成树
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 例1,利用凯莱递推法求下图生成树的棵数。 共8棵生成树

凯莱公式的缺点之一是计算量很大,其次是不能具 体指出每棵生成树。 2、关联矩阵计数法 定义3:n×m矩阵的一个阶数为mim{n,m}的子方阵, 称为它的一个主子阵;主子阵的行列式称为主子行列式。 显然,当n<m时,nXm矩阵 个主子阵。 定理3设Am是连通图G的基本关联矩阵的主子阵,则 Am非奇异的充分必要条件是相应于Am的列的那些边构 成G的一棵生成树。 证明:略
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 凯莱公式的缺点之一是计算量很大,其次是不能具 体指出每棵生成树。 2、关联矩阵计数法 定义3 :n×m矩阵的一个阶数为min{n, m}的子方阵, 称为它的一个主子阵;主子阵的行列式称为主子行列式。 显然,当n<m时,n×m矩阵 个主子阵。 n C m 定理3 设Am是连通图G的基本关联矩阵的主子阵,则 Am非奇异的充分必要条件是相应于Am的列的那些边构 成G的一棵生成树。 证明:略

该定理给出了求连通图G的所有生成树的方法: (1)写出G的关联矩阵,进一步写出基本关联矩阵, 记住参考点; (2)找出基本关联矩阵的非奇异主子阵,对每个这样 的主子阵,画出相应的生成树
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 该定理给出了求连通图G的所有生成树的方法: (1) 写出G的关联矩阵,进一步写出基本关联矩阵, 记住参考点; (2) 找出基本关联矩阵的非奇异主子阵,对每个这样 的主子阵,画出相应的生成树

(2)找出基本关联矩阵的非奇异主子阵,对每个这样 的主子阵,画出相应的生成树。 例2,画出下图G的所有不同的生成树。 G 解:取4为参考点,G的基本关联矩阵为: d 0 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 (2) 找出基本关联矩阵的非奇异主子阵,对每个这样 的主子阵,画出相应的生成树。 例2,画出下图G的所有不同的生成树。 1 2 3 4 a b c d e G 解:取4为参考点,G的基本关联矩阵为: 11000 01110 00011 Af abcde 1 2 3
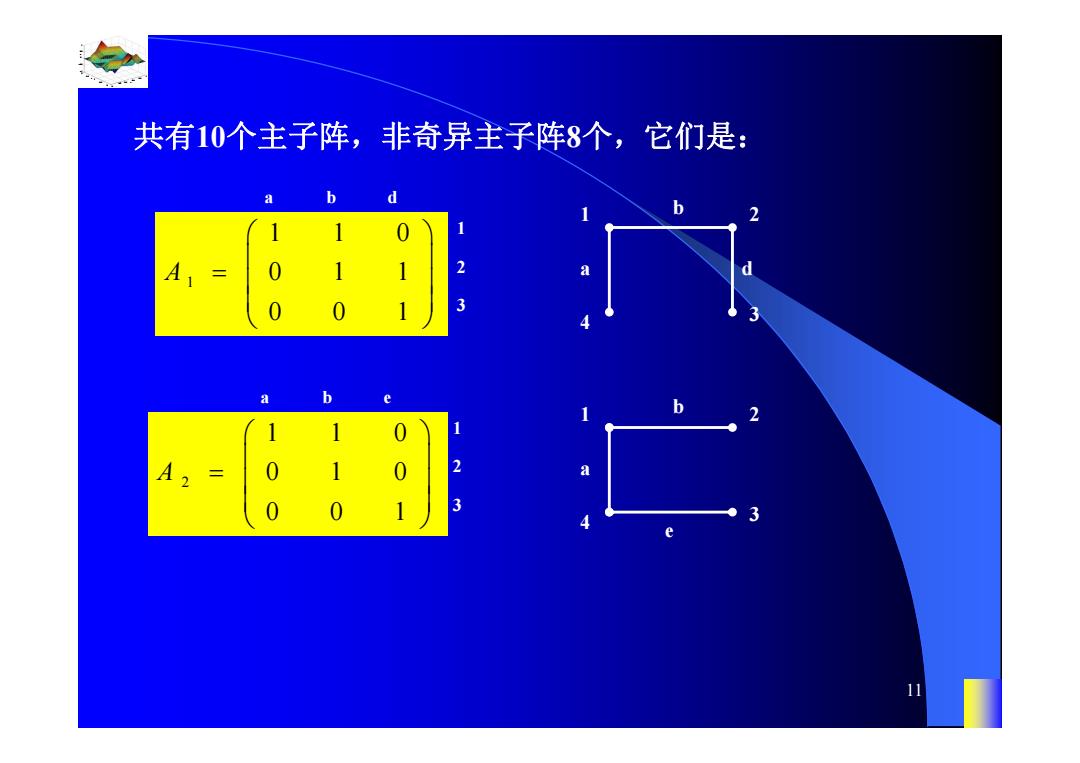
共有10个主子阵,非奇异主子阵8个,它们是: 11 11
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 共有10个主子阵,非奇异主子阵8个,它们是: 1 2 3 4 a b d 1 110 011 001 A abd 1 2 3 2 110 010 001 A abe 1 2 3 1 2 3 4 a b e