
Advanced Algorithms Concentration of Measure 尹一通Nanjing University,2022Fall
尹⼀通 Nanjing University, 2022 Fall Advanced Algorithms Concentration of Measure
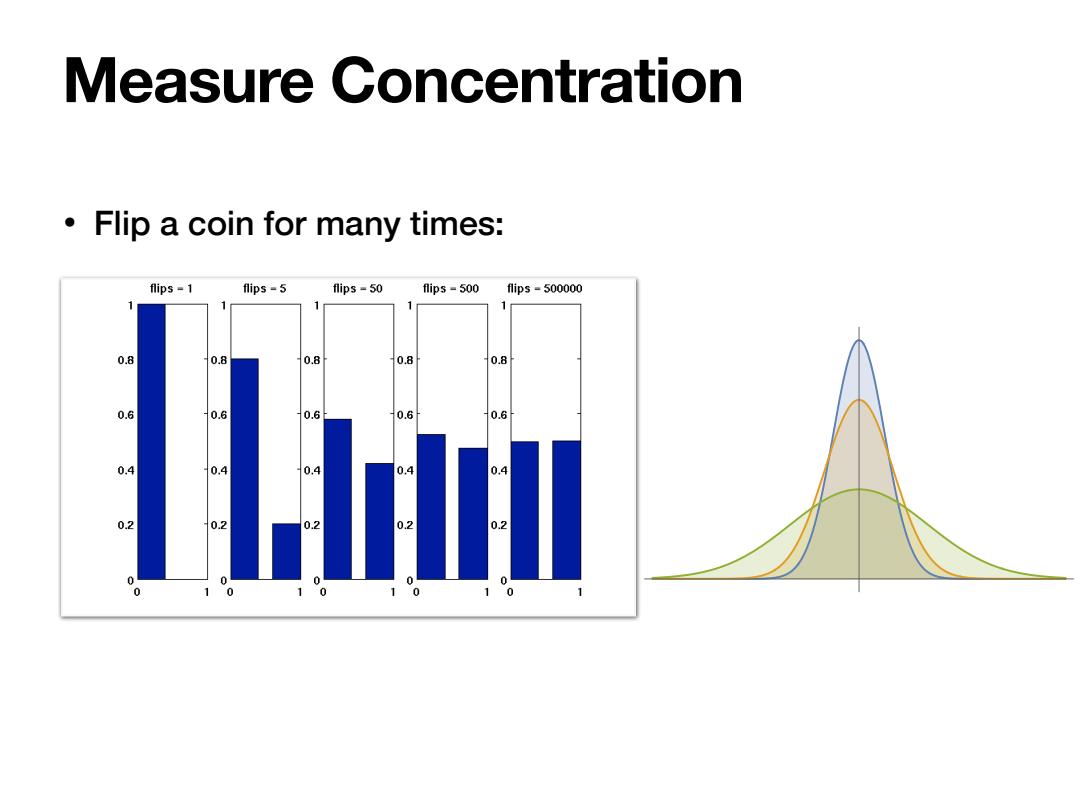
Measure Concentration Flip a coin for many times: flips-1 flips -5 flips 50 flips -500 fips-500000 0.8 10.8 0.8 0.8 0.8 0.6 0.6 0.6 0.6 0.6 0.4 0.4 0.4 0.4 0.4 0.2 0.2 0.2 0.2 0.2 0 0 0 0 0 0 0 0
• Flip a coin for many times: Measure Concentration

Chernoff-Hoeffding Bounds
Chernoff-Hoeffding Bounds

Chernoff Bound (Bernstein Inequalities) Life in Los Angeles 价 PLOY 《RBAN STRES T RATE MED MED. Herman Chernoff 品 Chernoff face
Chernoff Bound (Bernstein Inequalities) Herman Chernoff Chernoff face
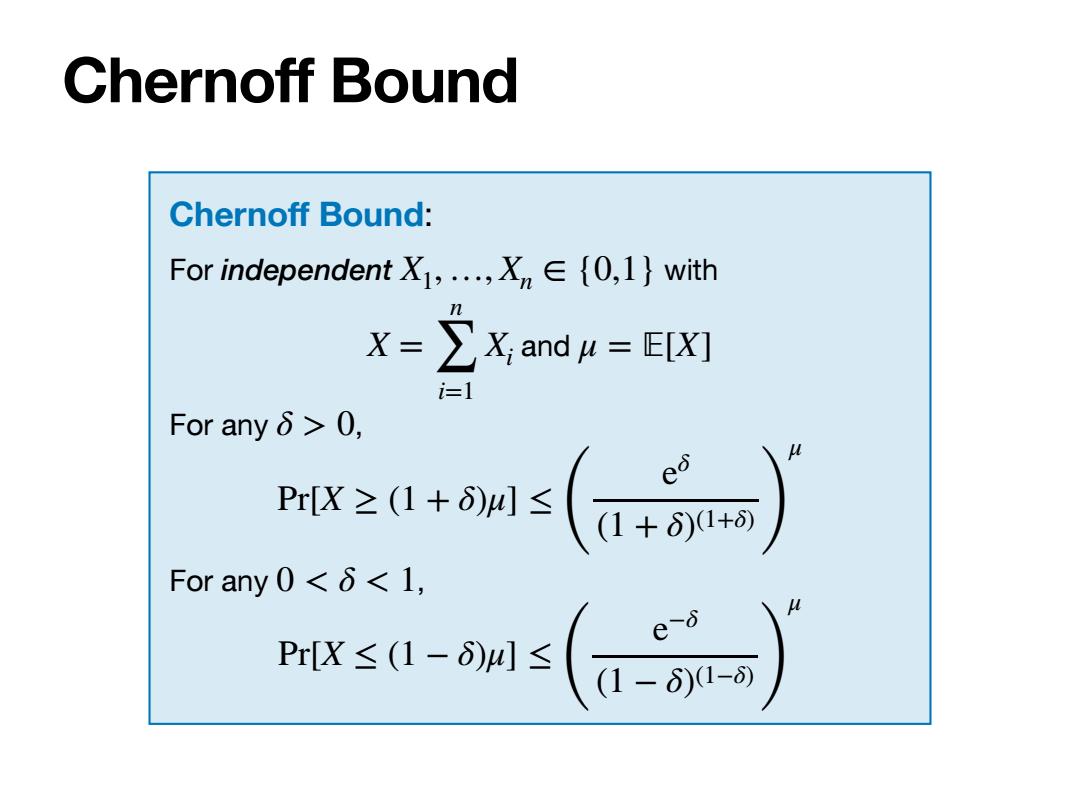
Chernoff Bound Chernoff Bound: For independent X,,Xn∈{0,l}with X=∑X,andu=E[X灯 i=1 For anyδ>0, e1os(可) For any 0<<1, Hirs0-(a-苏可》
Chernoff Bound Chernoff Bound: For independent with and For any , For any , X1, …, Xn ∈ {0,1} X = n ∑ i=1 Xi μ = 피[X] δ > 0 Pr[X ≥ (1 + δ)μ] ≤ ( eδ (1 + δ)(1+δ) ) μ 0 < δ < 1 Pr[X ≤ (1 − δ)μ] ≤ ( e−δ (1 − δ)(1−δ) ) μ
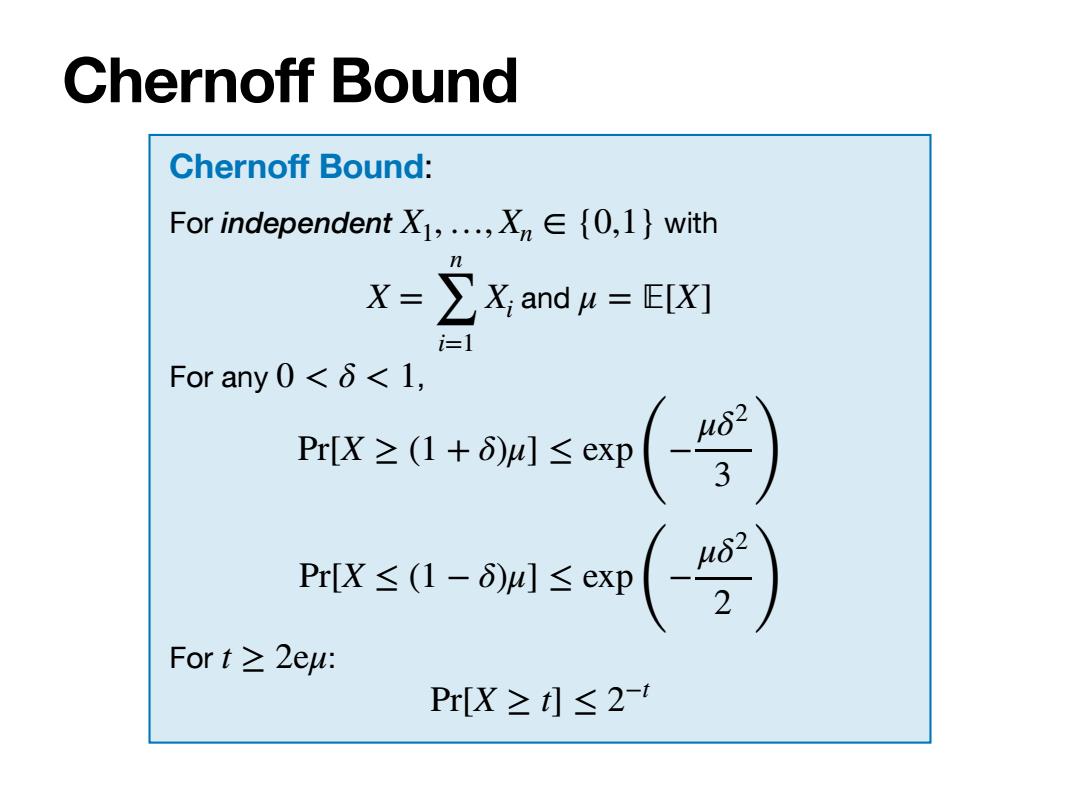
Chernoff Bound Chernoff Bound: For independent X1,,Xn∈{0,l}with X=∑X;andu=E[X] i=1 For any 0<<1, Pr[X≥(1+6)W≤ex (〉 Pr[X≤(1-δ)W川]≤exp Fort≥2eu: Pr[X≥1≤2-t
Chernoff Bound Chernoff Bound: For independent with and For any , For : X1, …, Xn ∈ {0,1} X = n ∑ i=1 Xi μ = 피[X] 0 < δ < 1 Pr[X ≥ (1 + δ)μ] ≤ exp (−μδ2 3 ) Pr[X ≤ (1 − δ)μ] ≤ exp (−μδ2 2 ) t ≥ 2eμ Pr[X ≥ t] ≤ 2−t

Balls into Bins m balls are thrown into n bins. X;:number of balls in the i-th bin [1 withprob,,为 whnereX 17 1 j=1 with prob.1 n m Xi~Bin(m,1/n) =E[X]= n Chernoff Bound:For 6>0, PrX,≥(1+4≤ ed a+
Balls into Bins m balls are thrown into n bins. X number of balls in the i-th bin i : X where i = m ∑ j=1 Xij Xij = 1 with prob. 1 n 0 with prob. 1 − 1 n Chernoff Bound: For δ > 0, Pr[Xi ≥ (1 + δ)μ] ≤ ( eδ (1 + δ)(1+δ) ) μ μ = 피[Xi ] = m n Xi ∼ Bin(m,1/n)
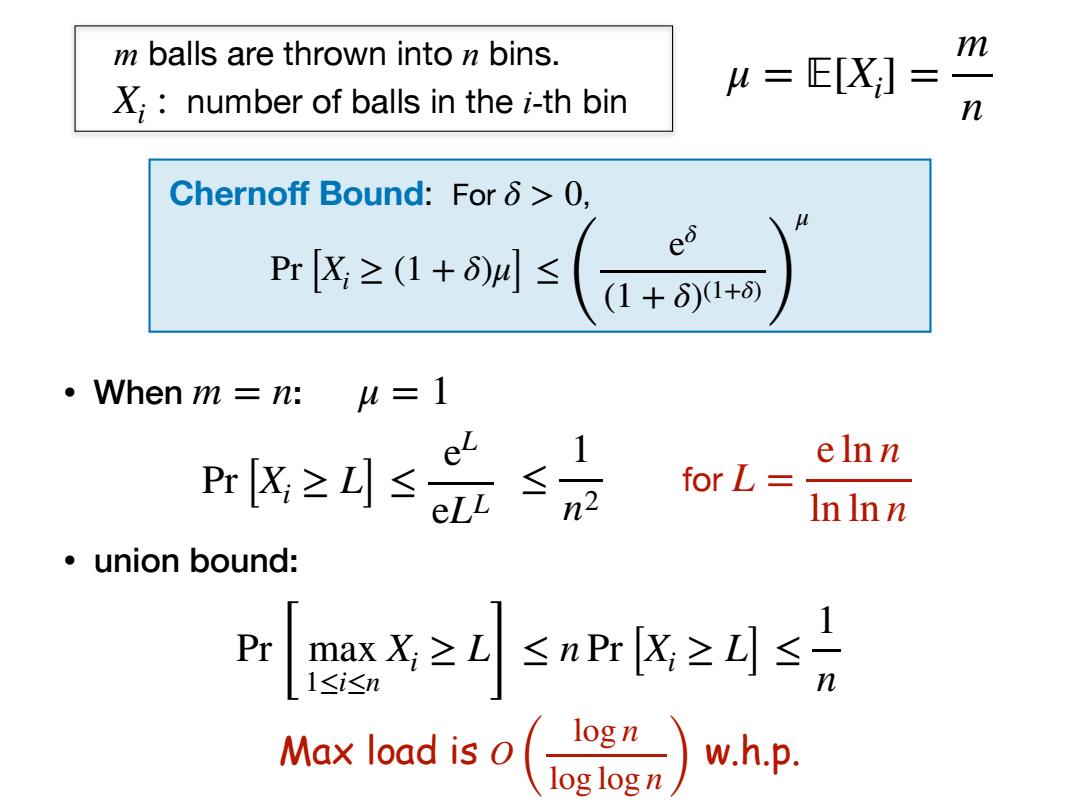
m balls are thrown into n bins. m E[X;]= X;:number of balls in the i-th bin n Chernoff Bound:For 6>0, Pr[X,≥(1+δ)4≤ ·When m=n:u=l ≥法 elnn for L= n2 In Inn 。union bound: n婴x≥sn民≥小s分 1<i≤n Max load is o logn loglogn w.h.p
m balls are thrown into n bins. X number of balls in the i-th bin i : μ = 피[Xi ] = m n • When : • union bound: m = n μ = 1 Pr[Xi ≥ L] ≤ eL eLL ≤ 1 n2 for L = e ln n ln ln n Pr [ max 1≤i≤n Xi ≥ L ] ≤ n Pr[Xi ≥ L] ≤ 1 n Max load is O w.h.p. ( log n log log n ) Chernoff Bound: For δ > 0, Pr[Xi ≥ (1 + δ)μ] ≤ ( eδ (1 + δ)(1+δ) ) μ

m balls are thrown into n bins. m =E[X]= X;:number of balls in the i-th bin n Chernoff Bound:For L>2eu, PrX≥L≤2b ·When m≥nlnn:u≥lnn k≥-mk≥s2w≤2" 1 n2 ·union bound: Pr 1≤i≤n 二 Max load is w.h.p
m balls are thrown into n bins. X number of balls in the i-th bin i : μ = 피[Xi ] = m n Chernoff Bound: For L ≥ 2eμ, Pr[Xi ≥ L] ≤ 2−L • When : • union bound: m ≥ n ln n μ ≥ ln n Pr [ Xi ≥ 2em n ] = Pr[Xi ≥ 2eμ] ≤ 1 n2 Pr [ max 1≤i≤n Xi ≥ 2em n ] ≤ n Pr [ Xi ≥ 2em n ] ≤ 1 n Max load is O w.h.p. ( m n ) ≤ 2−2eμ ≤ 2−2e ln n
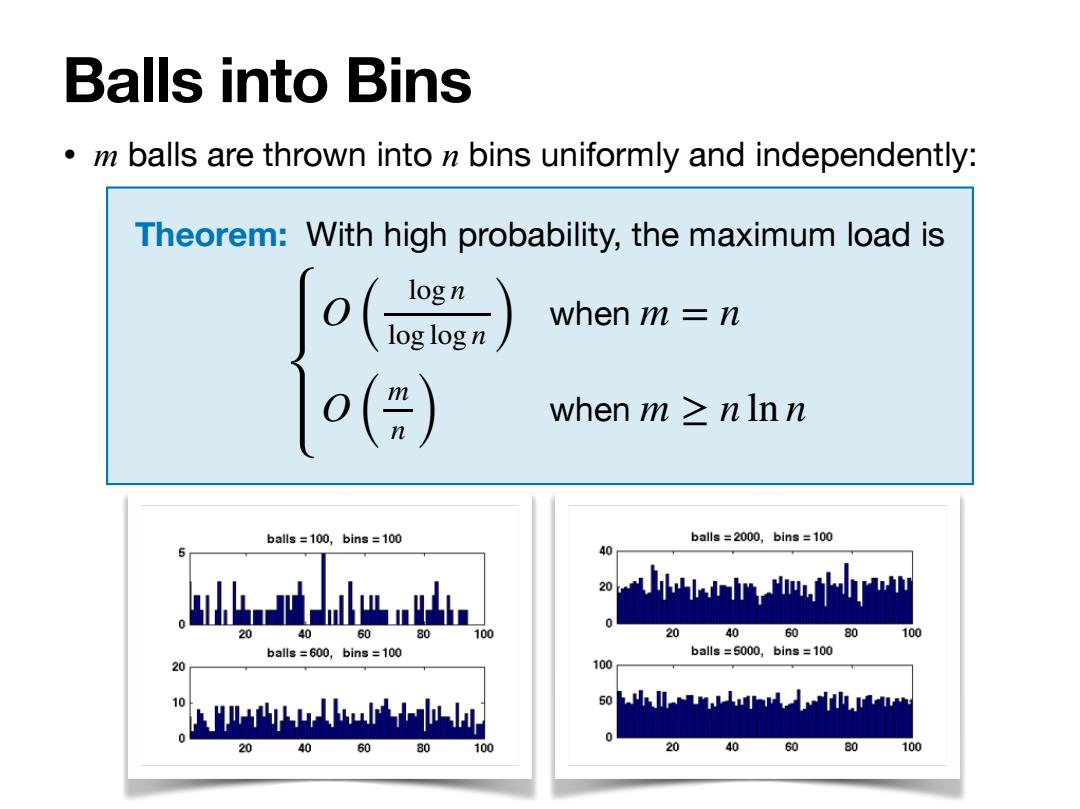
Balls into Bins m balls are thrown into n bins uniformly and independently: Theorem:With high probability,the maximum load is ∫o(=) when m =n o() when m≥nlnn balls =100,bins =100 balls =2000,bins =100 40 ek 20 dbkor wwlww 0 40 60 80 100 20 40 60 80 100 balls =600,bins =100 balls =5000,bins =100 20 100 10 arthb soLlaLitiuu 0 20 40 60 80 100 20 40 60 80 100
Theorem: With high probability, the maximum load is O ( log n log log n) when m = n O ( m n ) when m ≥ n ln n • m balls are thrown into n bins uniformly and independently: Balls into Bins