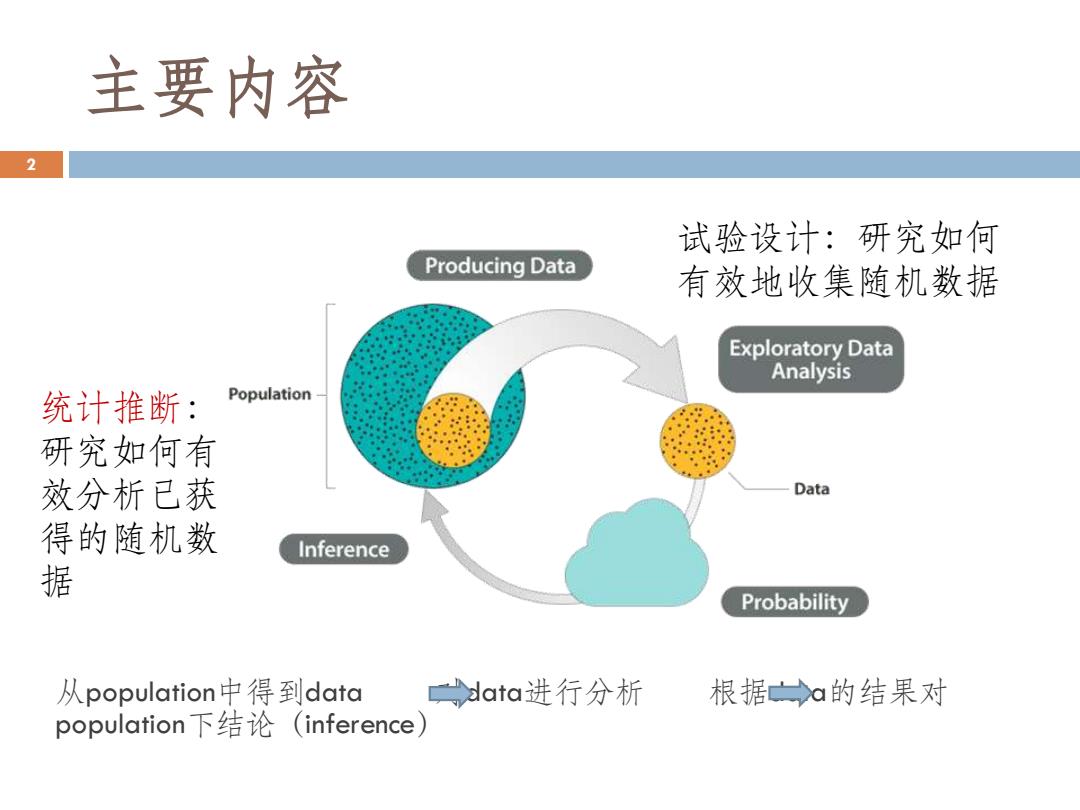
主要内容 2 试验设计:研究如何 Producing Data 有效地收集随机数据 Exploratory Data Analysis 统计推断: Population 研究如何有 效分析已获 Data 得的随机数 Inference 据 Probability 从population中得到data data进行分析 根据a的结果对 population下结论(inference)
2 从population中得到data 对data进行分析 根据data的结果对 population下结论(inference) 试验设计:研究如何 有效地收集随机数据 统计推断: 研究如何有 效分析已获 得的随机数 据 主要内容

关于试验设计 3 1936年罗斯福(Roosevelt)任总统第一任期满,共和党候选人当 登(Landon).绝大多数观察家认为罗斯福会不费力获胜.“文学摘 要”自1916年以来历届总统选举中,都正确地预测获胜者,这次根 据240万人的民意测验,预测兰登会以57%对43%获胜.但是,最后罗斯 福以62%对38%获胜.此后不久“文学摘要”就垮台了: 尽管样本足够大,但“文学摘要”预测误差大的惊人.盖洛普(Gallup)刚 刚成立调查机构,他在“文学摘要”之前,仅用3000人的样本,以一个百 分点的误差预言了“文学摘要”的结果.另外利用来源不同的5万人的 样本,正确地预测罗斯福获胜.盖洛普预测56%赞成罗斯福,误差=62% -56%=6%
关于试验设计 3

关于试验设计 4 “文学摘要”的差错在哪? (1)选择偏倚.他们抽取样本的程序:将问卷邮寄给1千万人,这1千 万人的名单和地址来自电话薄和俱乐部名册.这导致筛掉不属于俱 乐部和没有电话的穷人(当时1/4的家庭有电话).因此,有选择偏差. 1936年,绝大多数穷人投罗斯福的票,而富人投兰登的票. ②)不回答偏筑不回答者可能非常不同于回答者,“文学摘要收 到1千万人中的240万人的回答.调查得知:低收入和高收入的人倾向 不回答,中等收入阶层的回答居多. 现代调查机构更喜欢采用亲自询问代替邮寄问卷.亲自询问的典 型回答率是65%,而邮寄的典型回答率是25%
关于试验设计 4

统计推断的主要内容 5 ▣统计量与抽样分布 口参数估计 ▣假设检验
统计推断的主要内容 统计量与抽样分布 参数估计 假设检验 5

6 统计量与抽样分布
统计量与抽样分布 6

提纲 7 口基本概念 口正态总体的抽样分布 口有些分布对于统计意义较大 口正态分布、x分布、分布、F分布
提纲 基本概念 正态总体的抽样分布 有些分布对于统计意义较大 正态分布、χ 2分布、t分布、F分布 7

基本概念:总体与个体 8 总体:研究对象的某项数量指标的值的全体。 个体:总体中的每个元素为个体。 例如:某厂生产的灯泡寿命是总体,每一个灯泡的 寿命是个体;某学校全体男生的身高是总体,每个 男生的身高是个体。 研究对象的数量指标X的取值在客观上有一定 的分布,因此,可将其看做随机变量,它的分 布称为总体分布
基本概念:总体与个体 8 总体:研究对象的某项数量指标的值的全体。 个体:总体中的每个元素为个体。 例如:某厂生产的灯泡寿命是总体,每一个灯泡的 寿命是个体;某学校全体男生的身高是总体,每个 男生的身高是个体。 研究对象的数量指标𝑿的取值在客观上有一定 的分布,因此,可将其看做随机变量,它的分 布称为总体分布

基本概念:样本 样本:从总体中随机抽取的一些个体 抽样:抽得样本的过程 样本容量:样本中个体的数量 样本值:对样本观察得到的数值 样本的二重性: >就一次具体观察而言,样本值是确定的数 > 在不同的抽样下,样本值会发生变化,因 此可看做是随机变量
基本概念:样本 9 样本:从总体中随机抽取的一些个体 抽样:抽得样本的过程 样本容量:样本中个体的数量 样本值:对样本观察得到的数值 样本的二重性: ➢ 就一次具体观察而言,样本值是确定的数 ➢ 在不同的抽样下,样本值会发生变化,因 此可看做是随机变量

基本概念:样本 10 定义:设随机变量X的分布函数是F(因),若X1,,X, 是具有同一分布函数F的相互独立的随机变量, 则称X1,,Xm为从总体X中得到的容量为n的简 单随机样本,简称为样本,其观察值x1,,xm 称为样本值。 样本的两个特性(对抽样的要求): > 代表性:样本的每个分量X:与总体X具有 相同的分布 > 独立性:X1,X2,…,Xn相互独立
基本概念:样本 10 定义:设随机变量X的分布函数是F(x),若 1 , , X X n 是具有同一分布函数F的相互独立的随机变量, 则称 为从总体X中得到的容量为n的简 单随机样本,简称为样本,其观察值 称为样本值。 1 , , n x x 1 , , X X n 样本的两个特性(对抽样的要求): ➢ 代表性:样本的每个分量𝑿𝒊与总体𝑿具有 相同的分布 ➢ 独立性:𝑿𝟏,𝑿𝟐, … ,𝑿𝒏相互独立

基本概念:样本联合分布/密度 由定义知:若X,,Xn为X的一个样本,则X,,X, 的联合分布函数为: F(x,x)=ΠF(x) i=1 设X的密度为P(☒,则X1,,X,的联合概率 密度为: p(x,xn)=Πp(x) i=1
基本概念:样本联合分布/密度 11 由定义知:若 为X的一个样本, 则 的联合分布函数为: 1 , , X X n 1 , , X X n * 1 1 ( , , ) ( ) n n i i F x x F x = = 设X的密度为p(x),则 的联合概率 密度为: 1 , , X X n * 1 1 ( , , ) ( ) n n i i p x x p x = =