
1 生成树
生成树 1

回顾 2 口内容1:表达式的(逆)波兰记法 口内容2:二叉搜索树 口内容3:前缀码与Huffman编码
内容1:表达式的(逆)波兰记法 内容2:二叉搜索树 内容3:前缀码与Huffman编码 2 回顾

本节提要 口内容1:生成树及其构造方法 口内容2:最小生成树算法
内容1:生成树及其构造方法 内容2:最小生成树算法 本节提要

生成树 口定义:若图G的生成子图是树,则该子图称为G的 生成树。 口注:含有G的所有顶点的子图称为G的生成子图 口无向图G连通当且仅当G有生成树 口证明(充分性显然): →注意:若G是有简单回路的连通图,删除回路上的 一条边,G中的回路一定减少。(因此,用“破圈法” 总可以构造连通图的生成树) 口简单无向图G是树当且仅当G有唯一的生成树
生成树 定义:若图G的生成子图是树,则该子图称为G的 生成树。 注:含有G的所有顶点的子图称为G的生成子图 无向图G连通当且仅当G有生成树 证明(充分性显然): 注意:若G是有简单回路的连通图,删除回路上的 一条边,G中的回路一定减少。(因此,用“破圈法” 总可以构造连通图的生成树) 简单无向图G是树当且仅当 G有唯一的生成树

构造生成树:深度优先搜索 b b a a e d e d
构造生成树:深度优先搜索 a c b e d f a c b e d f

深度优先搜索算法 Procedure DFS(G:带顶点y,,yn的连通图) T:=只包含顶点y1的树; visit(v); Procedure visit(:G的J顶点) forv每个邻居w{ ifw不在T中then{ 加入顶点w和边{yw}到T; visit(w); }
深度优先搜索算法 Procedure DFS(G: 带顶点v1 ,…,vn的连通图) T:=只包含顶点v1的树; visit(v1 ); Procedure visit(v: G的顶点) for v每个邻居w { if w不在T中then { 加入顶点w和边{v,w}到T; visit(w); } }
回溯(八皇后) 在n×n格的棋盘上放置彼此不受攻击的n个皇后。 a b c d e f g h 从空棋盘开始 8 尝试第1列,第1行,n行; 曾 6 曾 尝试第2列,第1行,n行; 4 4 3 3 鬯 c3 尝试第k+1列,第1行,…n行; 警 1 d e
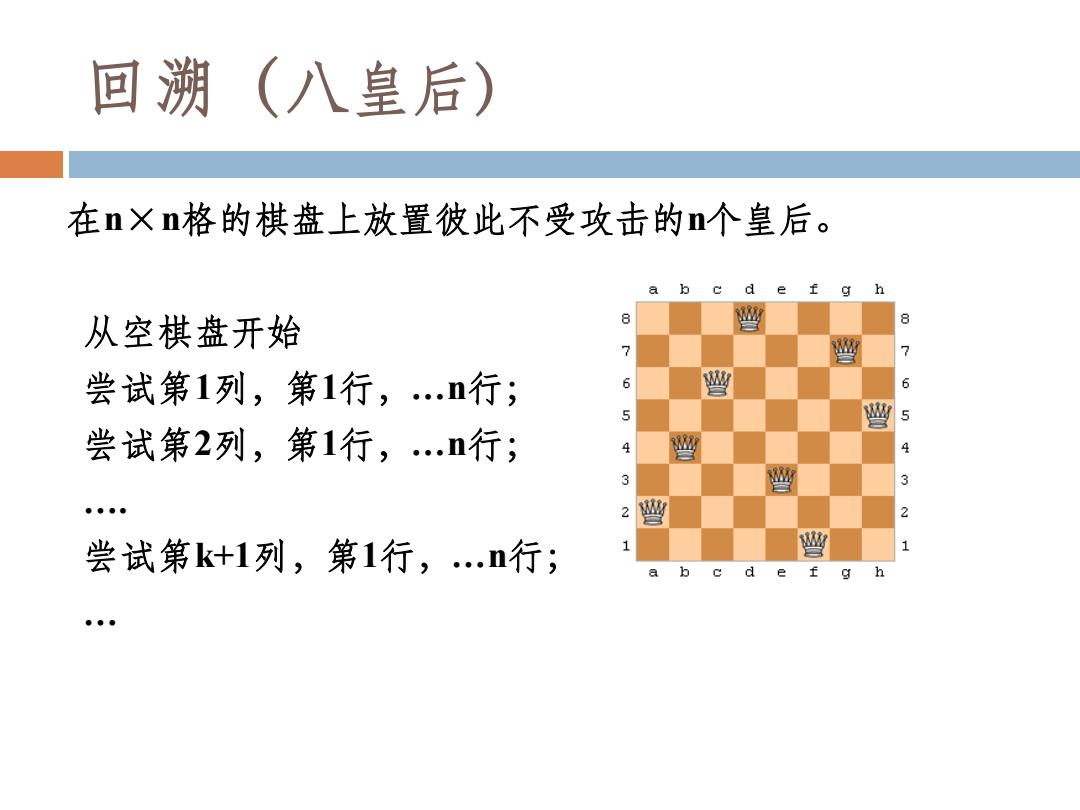
回溯(八皇后) 在n×n格的棋盘上放置彼此不受攻击的n个皇后。 从空棋盘开始 尝试第1列,第1行,…n行; 尝试第2列,第1行,…n行; …. 尝试第k+1列,第1行,…n行; …

回溯(子集和) 给定一组正整数x1,,Xn,和为M的一个子集? 从空子集开始 尝试添加一项, 和等于M,结束; 和不超过M,子集包含它; 没有合适添加项,去掉最后一项
回溯(子集和) 给定一组正整数x1 , …, xn,和为M的一个子集? 从空子集开始 尝试添加一项, 和等于M,结束; 和不超过M,子集包含它; 没有合适添加项,去掉最后一项
回溯(子集和) 举例:{31,27,15,11,7,5},和为39的子集? 31 {27乃 31,7} {31,5}{27,11} {27,7} 27,7,5}
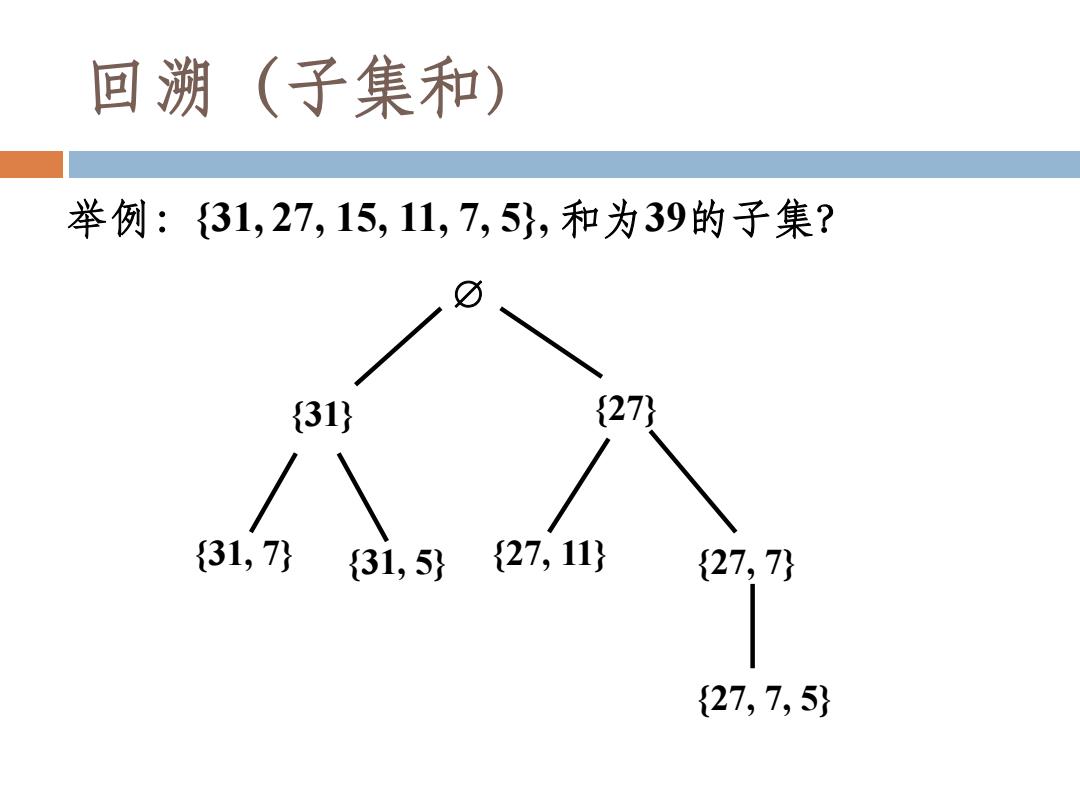
回溯(子集和) 举例:{31, 27, 15, 11, 7, 5}, 和为39的子集? {31} {27} {27, 7} {27, 11} {31, 5} {31, 7} {27, 7, 5}
构造生成树:广度优先搜索 b b a d a e e d
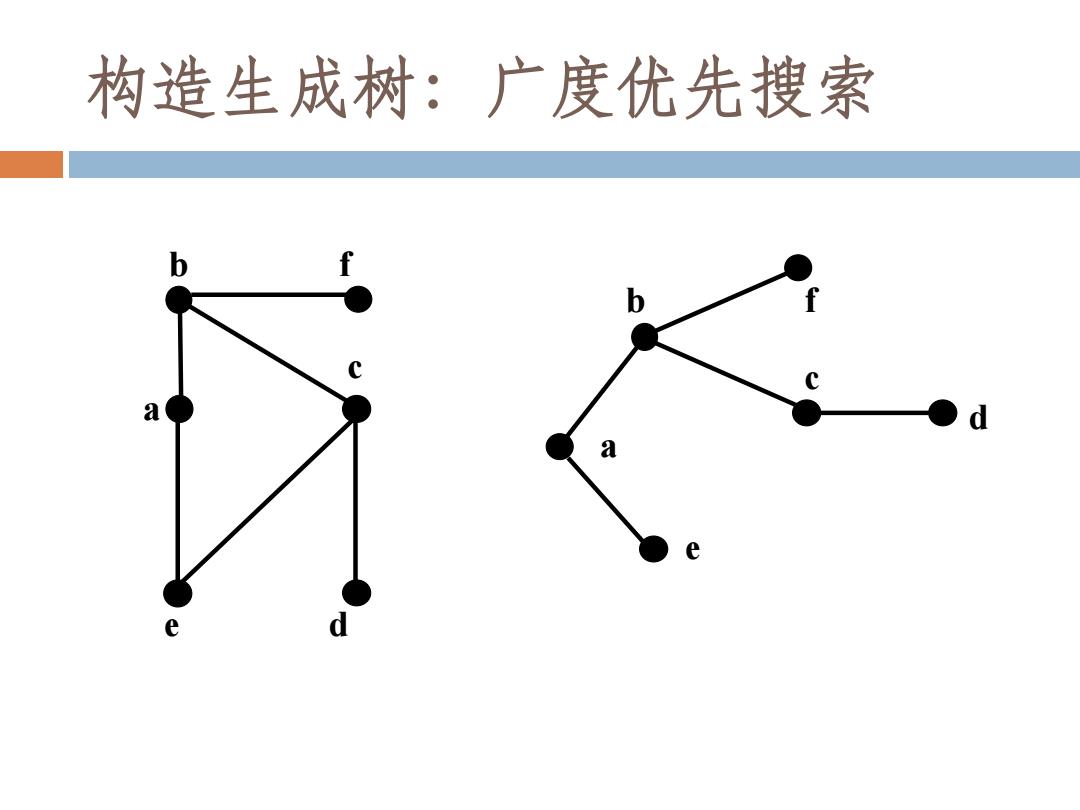
构造生成树:广度优先搜索 a b e d c f a c b e d f