
1 离散概率
离散概率 1

回顾 口内容1:容斥原理 ▣|AUBUC=|A|+|B+|C-|A⌒B|-|A⌒C |B∩C+|A⌒B∩C 口内容2:鸽笼原理 口n只鸽子放到m个笼子中,且m<n则至少有一个笼子 要装2个或多个 口内容3:排列与组合 口组合与二项式定理、组合计数方法、圆排列、不可区分 物的排列、是否允许重复等
内容1:容斥原理 |ABC|=|A|+|B|+|C|-|AB|-|AC|- |BC|+|ABC| 内容2:鸽笼原理 n 只鸽子放到m 个笼子中, 且 m<n, 则至少有一个笼子 要装2个或多个 内容3:排列与组合 组合与二项式定理、组合计数方法、圆排列、不可区分 物的排列、是否允许重复等 回顾

本节提要 口内容1:概率论 ▣内容2:贝叶斯定理 口内容3:随机变量及其期望与方差
内容1:概率论 内容2:贝叶斯定理 内容3:随机变量及其期望与方差 本节提要

例:生日问题 4 有k个人,设每个人的生日是365天的任何一天 是等可能的,求至少两人生日相同的概率。 解:令E={至少两人生日相同},则 E=k个人生日均不同} 显然,Pr(E)= (365)k 365k 故Pr(E)=1-Pr(E)=1- (365)k 365k
例:生日问题 有𝒌个人,设每个人的生日是365天的任何一天 是等可能的,求至少两人生日相同的概率。 解:令𝑬 = {至少两人生日相同},则 𝑬ഥ = 𝒌个人生日均不同 . 显然,𝑷𝒓 𝑬ഥ = 𝟑𝟔𝟓 𝒌 𝟑𝟔𝟓𝒌 . 故𝑷𝒓 𝑬 = 𝟏 − 𝑷𝒓 𝑬ഥ = 𝟏 − 𝟑𝟔𝟓 𝒌 𝟑𝟔𝟓𝒌 . 4
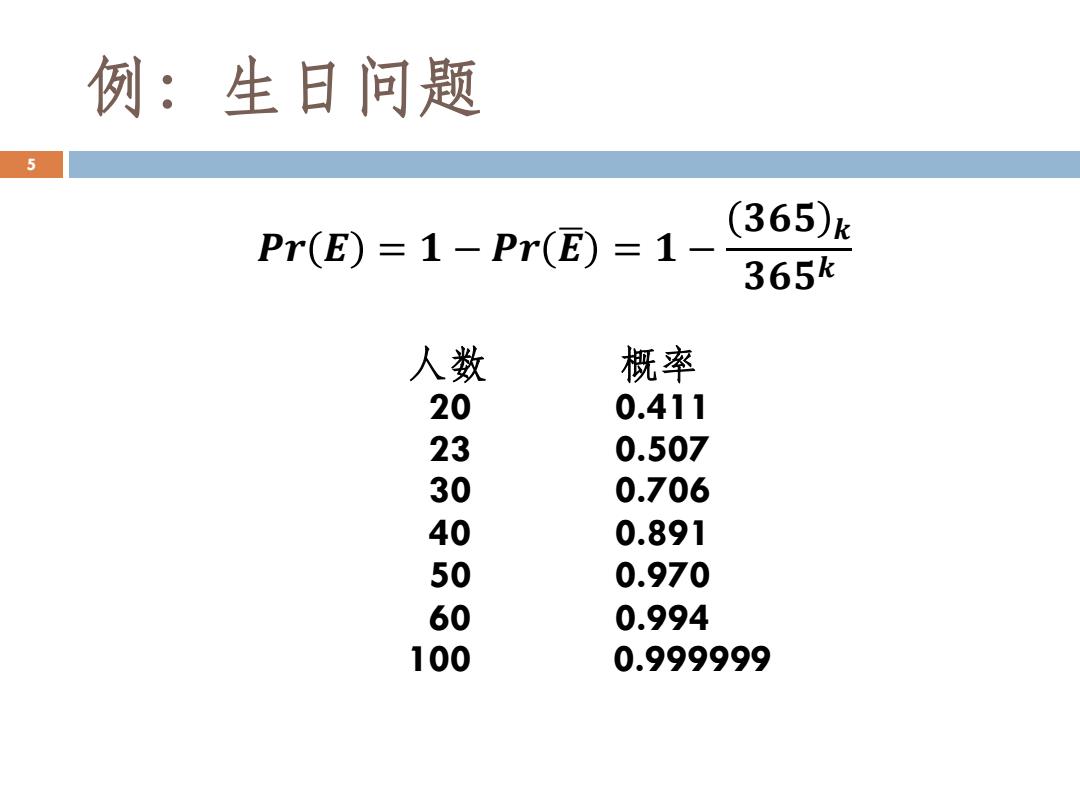
例:生日问题 5 Pr(E)=1-Pr(E)=1- (365)k 365k 人数 概率 20 0.411 23 0.507 30 0.706 40 0.891 50 0.970 60 0.994 100 0.999999
例:生日问题 𝑷𝒓 𝑬 = 𝟏 − 𝑷𝒓 𝑬ഥ = 𝟏 − 𝟑𝟔𝟓 𝒌 𝟑𝟔𝟓 𝒌 人数 概率 20 0.411 23 0.507 30 0.706 40 0.891 50 0.970 60 0.994 100 0.999999 5

基于集合论给概率以数学定义 口定义:可数样本空间S乃一个可数集合。 口S的每一个元素ω称为一个结果。 口定义:满足下列条件的函数Pr:S→R称为样本 空间S上的一个概率函数: Vwes Pr[w]≥0,且 ▣∑o∈5Pr[w]=1. ▣定义:S的一个子集E≤S称为一个事件。 口事件E的概率Pr[E]:=∑o∈EPr[ω]
定义:可数样本空间 𝒮 乃一个可数集合。 𝒮 的每一个元素 𝜔 称为一个结果。 定义:满足下列条件的函数 Pr: 𝒮 → ℝ 称为样本 空间 𝒮 上的一个概率函数: ∀𝜔∈𝒮 Pr 𝜔 ≥ 0 ,且 Σ𝜔∈𝒮 Pr 𝜔 = 1. 定义:𝒮 的一个子集 𝐸 ⊆ 𝒮 称为一个事件。 事件 E 的概率 Pr 𝐸 ∷= σ𝜔∈𝐸 Pr[𝜔] 基于集合论给概率以数学定义

基于集合论的概率计算 定理1:设E是样本空间S中的一个事件,事 件E(事件E的补事件)的概率为: Pr[E]=1-Pr[E] 定理2:设E1和E2是样本空间S中的事件, 那么: Pr[EUE2]=Pr[E]Pr[E2]Pr[E1 0 E2]
定理 1:设 𝐸 是样本空间 𝒮 中的一个事件,事 件 𝐸ത(事件 𝐸 的补事件)的概率为: Pr 𝐸ത = 1 − Pr[𝐸] 定理2:设 𝐸1 和 𝐸2 是样本空间 𝒮 中的事件, 那么: Pr 𝐸1 ∪ 𝐸2 = Pr 𝐸1 + Pr 𝐸2 − Pr[𝐸1 ∩ 𝐸2 ] 基于集合论的概率计算

均匀分布 定义:假设S是一个含n个元素的样本空间.均 匀分布(uniform distribution)赋给S中每个结果 1/n的概率. a举例:对于均匀的硬币Pr[团=PmT= ▣举例:公平的散子PrW=名,X=1…6 均匀分布下事件的概率可通过对其中的元素计 数求得
定义:假设𝒮是一个含 n 个元素的样本空间. 均 匀分布 (uniform distribution) 赋给 𝒮 中每个结果 1/n 的概率. 举例:对于均匀的硬币 Pr 𝐻 = Pr 𝑇 = 1 2 举例:公平的骰子Pr 𝑋 = 1 6 , 𝑋 = 1 ⋯ 6 均匀分布下事件的概率可通过对其中的元素计 数求得 均匀分布
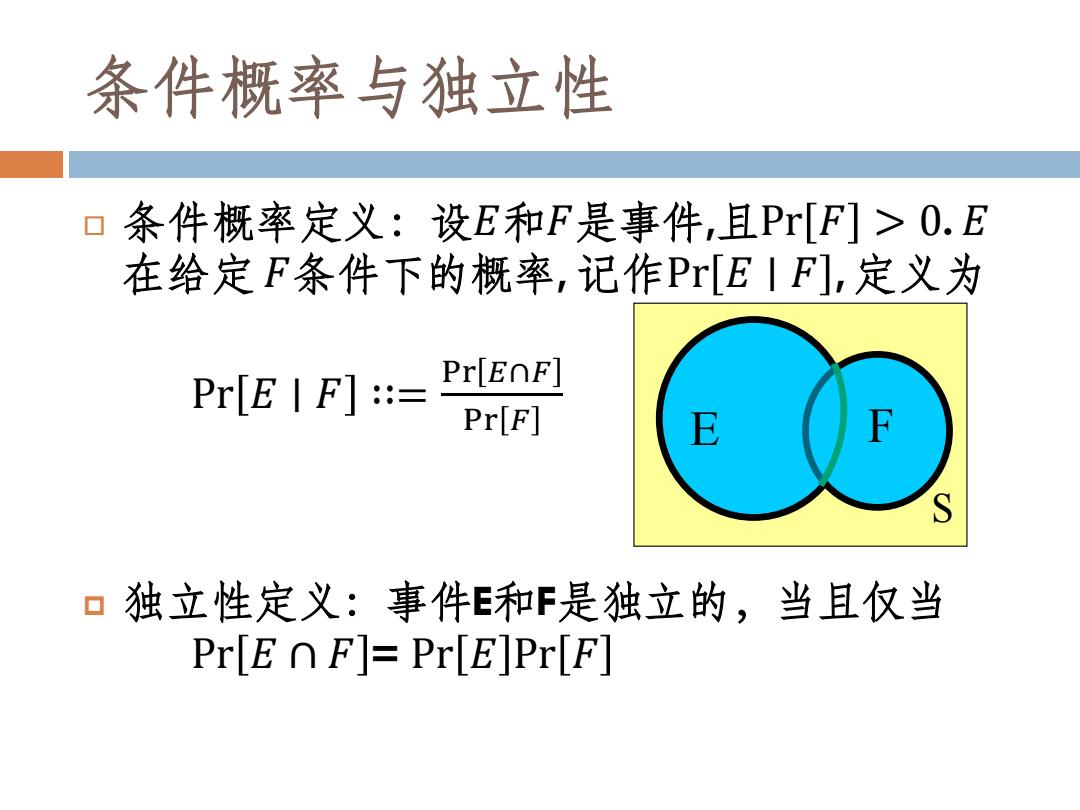
条件概率与独立性 条件概率定义:设E和F是事件,且Pr[F]>0.E 在给定F条件下的概率,记作Pr[E|F],定义为 Pr[E |F]:= Pr[EOF] Pr(F] S 口独立性定义:事件E和F是独立的,当且仅当 PrE nF]=PrE]Pr F]
条件概率定义:设𝐸和𝐹是事件,且Pr 𝐹 > 0. 𝐸 在给定 𝐹条件下的概率, 记作Pr 𝐸 ∣ 𝐹 , 定义为 Pr 𝐸 ∣ 𝐹 ∷= Pr 𝐸∩𝐹 Pr 𝐹 独立性定义:事件E和F是独立的,当且仅当 Pr 𝐸 ∩ 𝐹 = Pr 𝐸 Pr 𝐹 条件概率与独立性 S E F

例 10 在至少有一个男孩的条件下,有两个孩子的家 庭正好均是男孩的条件概率?假设BB,BG,GB, 和GG是等可能的。 解:令E是家庭有两个男孩的事件,F是家庭至少有一 个男孩的事件。我们有E={BB,F={BB,BG,GB}, E∩F={BB. ▣p(F)=3/4,p(EnF)=1/4. 因此,p(EE)= p(EnF) 1/4 1 p(F) 3/4=3
例 在至少有一个男孩的条件下,有两个孩子的家 庭正好均是男孩的条件概率?假设BB, BG, GB, 和GG是等可能的。 10