
1 树的应用
树的应用 1

回顾 口内容1:树的定义及其性质 口树就是不包含简单回路的连通无向图 口树是边最少的连通图;也是边最多的无简单回路的图 口内容2:根树以及有序根树的遍历 口根数:一个入度为0的顶点,其它顶点入度均为1 口完全树、平衡树、有序树 口有序根树的前中后遍历
内容1:树的定义及其性质 树就是不包含简单回路的连通无向图 树是边最少的连通图;也是边最多的无简单回路的图 内容2:根树以及有序根树的遍历 根数:一个入度为0的顶点,其它顶点入度均为1 完全树、平衡树、有序树 有序根树的前中后遍历 回顾

本节提要 3 口内容1:表达式的(逆)波兰记法 口内容2:二叉搜索树 口内容3:前缀码与Huffman编码
内容1:表达式的(逆)波兰记法 内容2:二叉搜索树 内容3:前缀码与Huffman编码 3 本节提要
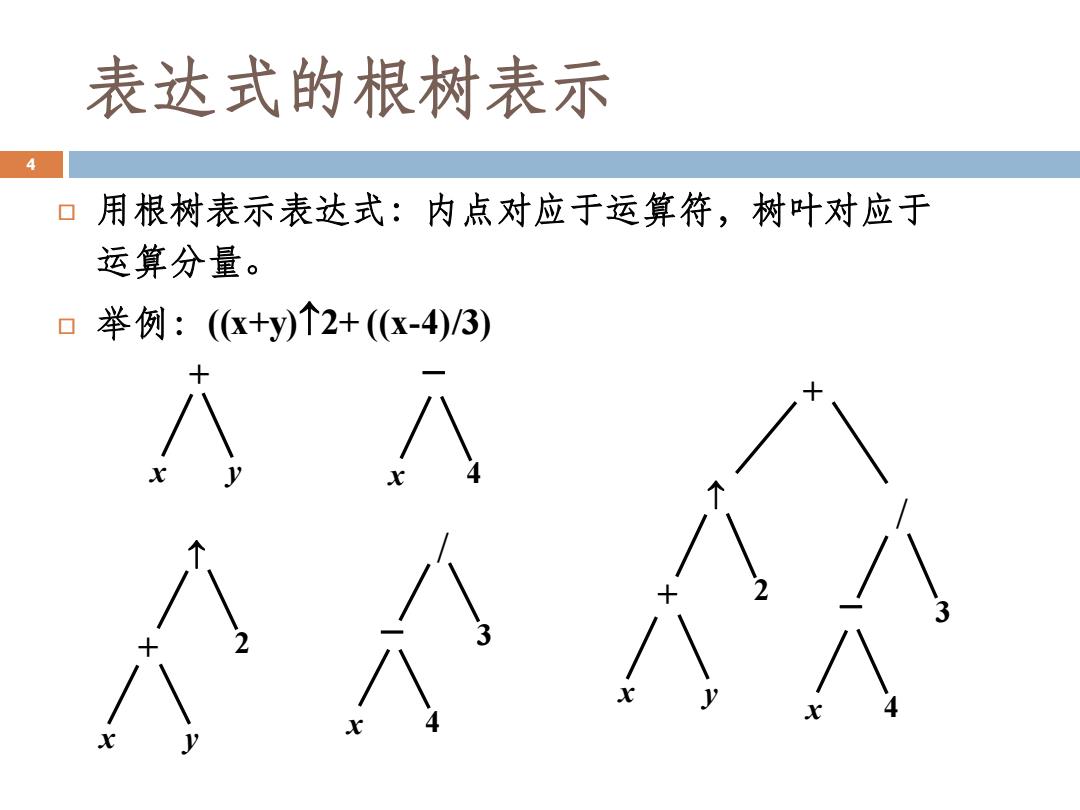
表达式的根树表示 用根树表示表达式:内点对应于运算符,树叶对应于 运算分量。 ▣举例:(x+y)个2+(x-4)/3)
用根树表示表达式:内点对应于运算符,树叶对应于 运算分量。 举例:((x+y)2+ ((x-4)/3) x y + 2 x + y x 4 − x 4 − 3 / 2 x + y x 4 − 3 / + 4 表达式的根树表示
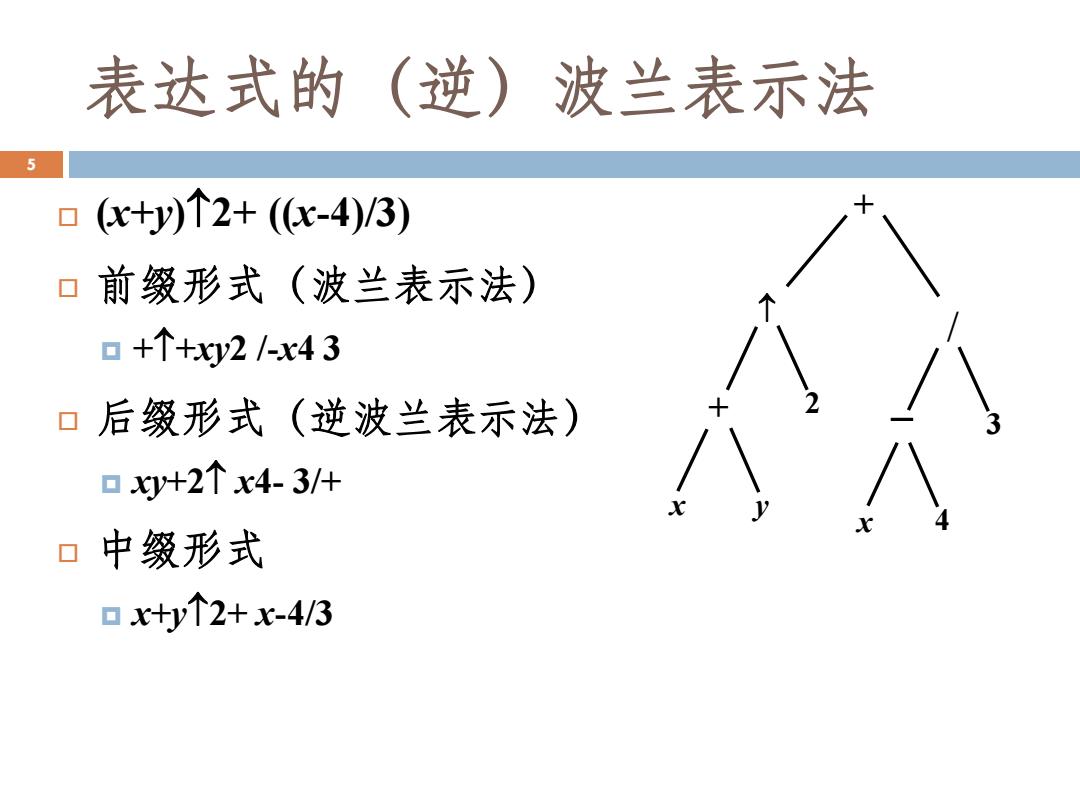
表达式的(逆)波兰表示法 5 口x+y)个2+(c-4)/3) 口前缀形式(波兰表示法) 口+个+y2/-x43 口后缀形式(逆波兰表示法) 口y+2个x4-3/+ 口中缀形式 口x+y个2+-4/3
(x+y)2+ ((x-4)/3) 前缀形式(波兰表示法) ++xy2 /-x4 3 后缀形式(逆波兰表示法) xy+2 x4- 3/+ 中缀形式 x+y2+ x-4/3 2 x + y x 4 − 3 / + 5 表达式的(逆)波兰表示法
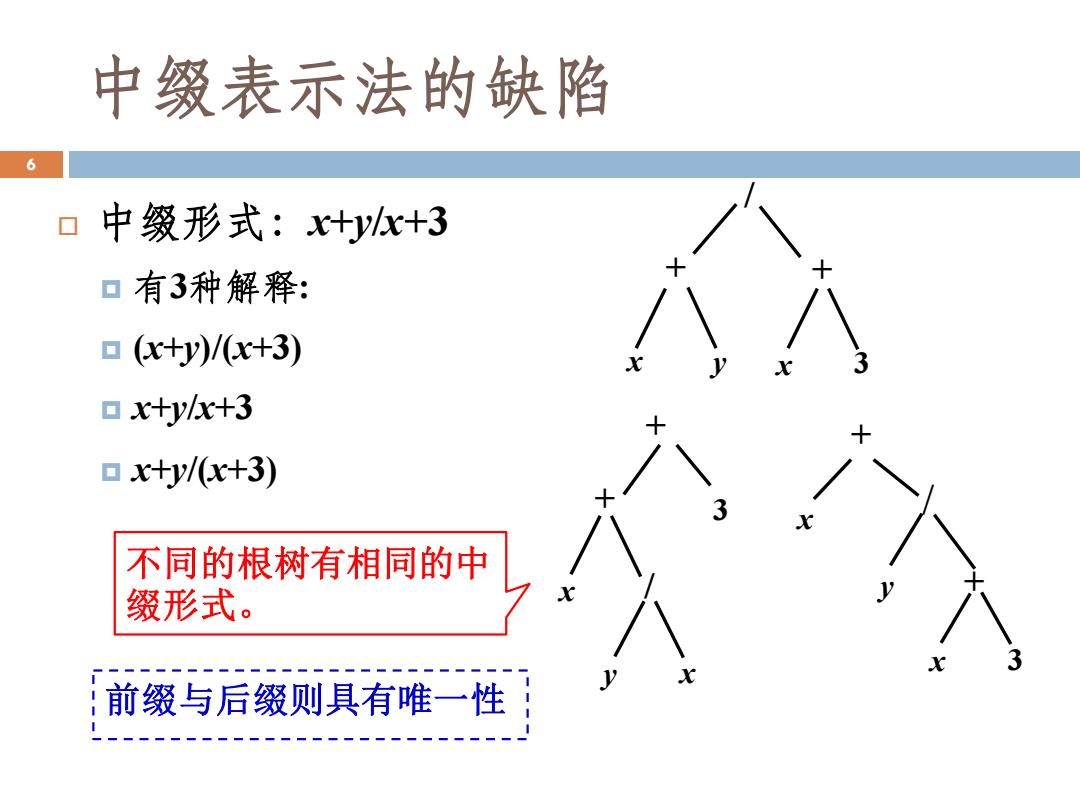
中缀表示法的缺陷 6 口中缀形式:x+yk+3 口有3种解释: ▣(x+y)/(x+3) ▣x+yx+3 ▣x+y/(x+3) 不同的根树有相同的中 缀形式。 X 3 前缀与后缀则具有唯一性
中缀形式:x+y/x+3 有3种解释: (x+y)/(x+3) x+y/x+3 x+y/(x+3) x + y / x 3 + 3 x + y x / + x 3 + / y x + 不同的根树有相同的中 缀形式。 前缀与后缀则具有唯一性 6 中缀表示法的缺陷
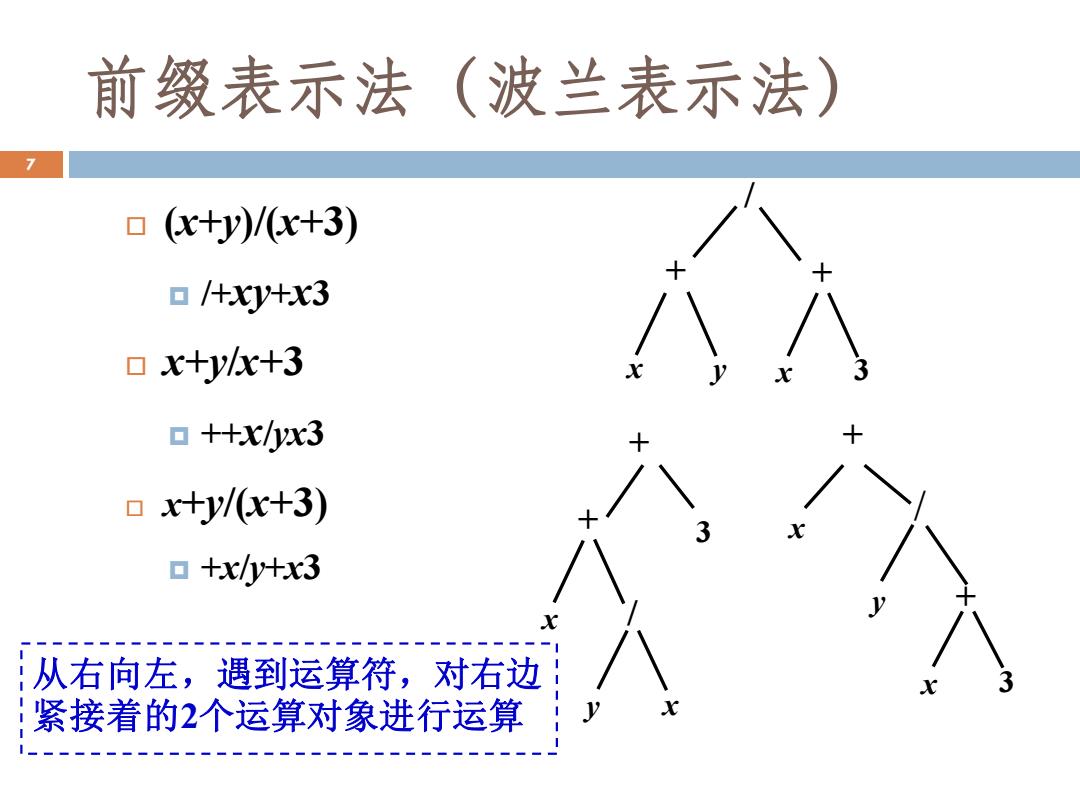
前缀表示法(波兰表示法) ▣(c+y)/(x+3) ▣/+Xy+x3 ▣x+yx+3 ▣++Xhx3 ▣x+y/(x+3) ▣+xy+x3 从右向左,遇到运算符,对右边 紧接着的2个运算对象进行运算
(x+y)/(x+3) /+xy+x3 x+y/x+3 ++x/yx3 x+y/(x+3) +x/y+x3 x + y / x 3 + 3 x + y x / + x 3 + / y x + 从右向左,遇到运算符,对右边 紧接着的2个运算对象进行运算 7 前缀表示法(波兰表示法)
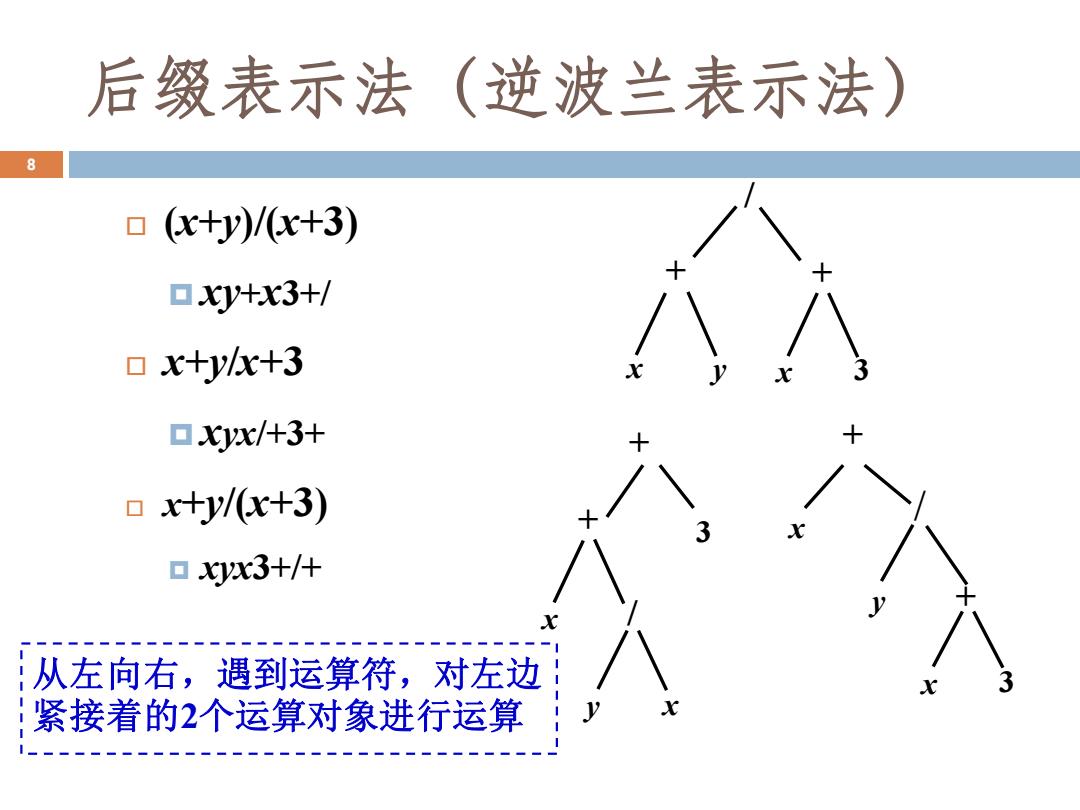
后缀表示法(逆波兰表示法) 8 ▣(c+y)/(x+3) ▣Xy+x3+/ ▣x+yx+3 ▣Xx/+3+ ▣x+y/(x+3) ▣x3+/+ 从左向右,遇到运算符,对左边 紧接着的2个运算对象进行运算
(x+y)/(x+3) xy+x3+/ x+y/x+3 xyx/+3+ x+y/(x+3) xyx3+/+ x + y / x 3 + 3 x + y x / + x 3 + / y x + 从左向右,遇到运算符,对左边 紧接着的2个运算对象进行运算 8 后缀表示法(逆波兰表示法)
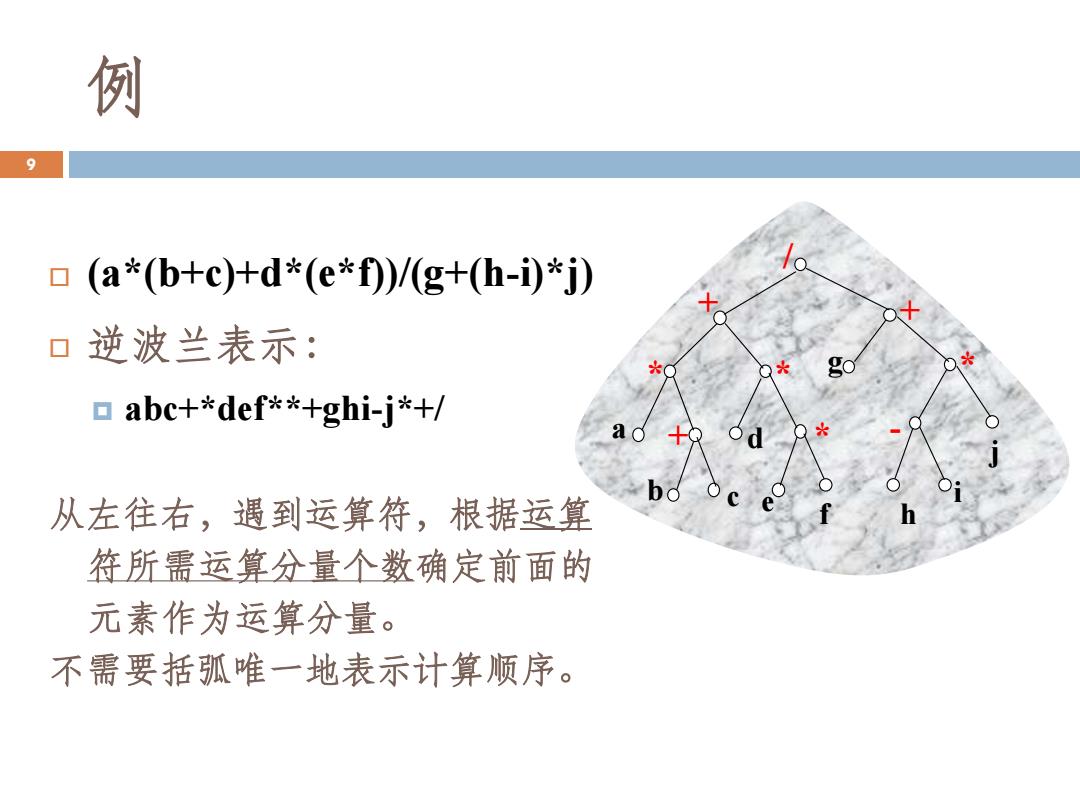
例 9 o (a*(b+c+d*(e*f)/g+(h-i)*j) 0 逆波兰表示: abc+*def**+ghi-j*+/ 从左往右,遇到运算符,根据运算 符所需运算分量个数确定前面的 元素作为运算分量。 不需要括弧唯一地表示计算顺序
(a*(b+c)+d*(e*f))/(g+(h-i)*j) 逆波兰表示: abc+*def**+ghi-j*+/ 从左往右,遇到运算符,根据运算 符所需运算分量个数确定前面的 元素作为运算分量。 不需要括弧唯一地表示计算顺序。 j i a g b c d e f h / + + * * * + * - 9 例

例 10 后缀表达式求值:723*4个93/+ 26二4个931+ L4个931+ 193/+ 4
7 2 3 * - 4 9 3 / + 7 6 - 4 9 3 / + 1 4 9 3 / + 4 1 9 3 / + 1 3 + 10 例 后缀表达式求值: