南京大学：《离散数学》课程教学资源（PPT课件讲稿）Lecture 09 计数

1 计数

计数 1

本节提要 口内容1：容斥原理 口内容2：鸽笼原理 口内容3：排列与组合

 内容1：容斥原理  内容2：鸽笼原理  内容3：排列与组合 本节提要

两个有限集合并集的计数 已知某个班级学英语的50 人，学法语的30人，分别 E 记为： E⌒F |E=50,1F|=30 问这个班级一共多少人？ 显然，只要E⌒F地，班级 人数就并非80人。 既学英语，又学法语的同学 EUF|=(IE|+|FI)-IE⌒F

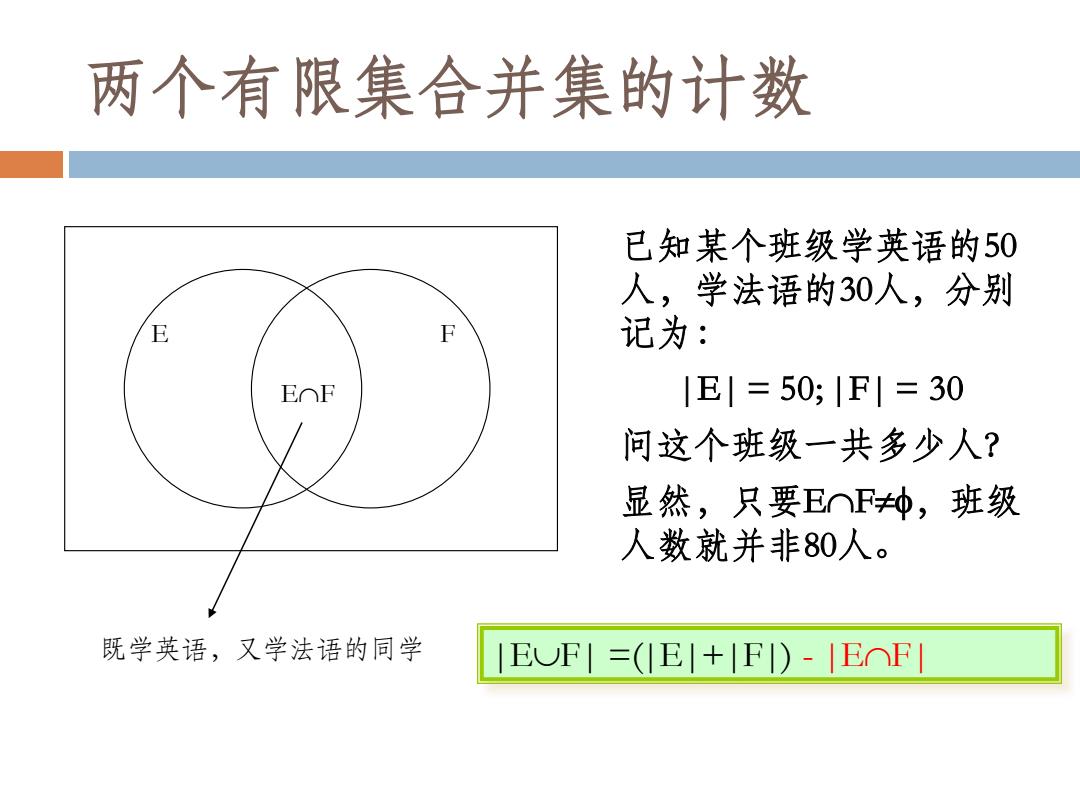
两个有限集合并集的计数 既学英语，又学法语的同学 E F EF 已知某个班级学英语的50 人，学法语的30人，分别 记为： |E| = 50; |F| = 30 问这个班级一共多少人？ 显然，只要EF，班级 人数就并非80人。 |EF| =(|E|+|F|) - |EF|

数字排列的例子 将0,1,2，，9排成一列，要求第1个数字大于1，最后一 个数字小于8，共有多少种排法？ 口这10个数字所有的排法构成全集U,|U1=10! 口第1个数字不大于1的排法构成子集A(即所有以0或者1开头的排法)， |A=29I 口最后一个数字不小于8的排法构成子集B(即所有以8或者9结束的 排法)，|B|=29列 ▣|A⌒B|=228! 口题目要求的排法构成子集(~A⌒~B) ▣I(~A⌒~B)1=IU|-IAUB|=IU|-|A|-|B|+IA∩B|=10I -4◆91+4◆81=2,338,560

数字排列的例子  将0,1,2,...,9排成一列，要求第1个数字大于1，最后一 个数字小于8，共有多少种排法？  这10个数字所有的排法构成全集U, |U|=10!  第1个数字不大于1的排法构成子集A(即所有以0或者1开头的排法), |A|=29!  最后一个数字不小于8的排法构成子集B(即所有以8或者9结束的 排法), |B|=29!  |AB|=228!  题目要求的排法构成子集(~A~B)  |(~A~B)| = |U| - |AB| = |U| -|A| - |B| + |AB| = 10! - 49! + 48! = 2,338,560

三个有限集合并集的计数 口假设定义全集的三个子集A,B,C。则： AUBOCI=|A|+IB|+|C-|A∩B|-IA⌒C-|B⌒CI+|A⌒B⌒CI 证明： IAUBUCI=AUB+CI-(AUB)OC =|A|+IB|-|A⌒B|+ICl-I(A⌒C)火UB⌒C)I =|A|+|B|-|A⌒B|+ICl-I(A⌒C)川-IB⌒C)|+I(A⌒B∽C)I =|A|+|B|+|C-|A⌒B|-|A⌒C-IB⌒C+|A⌒B∽C

三个有限集合并集的计数  假设定义全集的三个子集A,B,C。则： |ABC|=|A|+|B|+|C|-|AB|-|AC|-|BC|+|ABC| 证明： |ABC|=|AB|+|C|-|(AB)C| =|A|+|B|-|AB|+|C|-|(AC)(BC)| =|A|+|B|-|AB|+|C| - |(AC)|-|(BC)|+|(ABC)| =|A|+|B|+|C|-|AB|-|AC|-|BC|+|ABC|

选课的例子 口全班共有160个学生 口选数学课64人，选计算机课94人，选金融课58人 口选数学与金融的28人，选数学与计算机的26人，选 计算机与金融的22人 口三种课全选的14人。 问：这三种课都没选的是多少？只选一门计算 机的有多少？

选课的例子  全班共有160个学生  选数学课64人，选计算机课94人，选金融课58人  选数学与金融的28人，选数学与计算机的26人，选 计算机与金融的22人  三种课全选的14人。  问：这三种课都没选的是多少？只选一门计算 机的有多少？

选课的例子 8 M-数学、C-计算机、F金融 口容斥原理 6 M 24 MUCUF=M+C+F- M⌒F|-|M∽Cl-ICF|+ IM⌒C⌒FI 12 14 14 =64+94+58-28-26-22+14 =154 60 8 22 因此，6人未选课。 只选了计算机课的60人

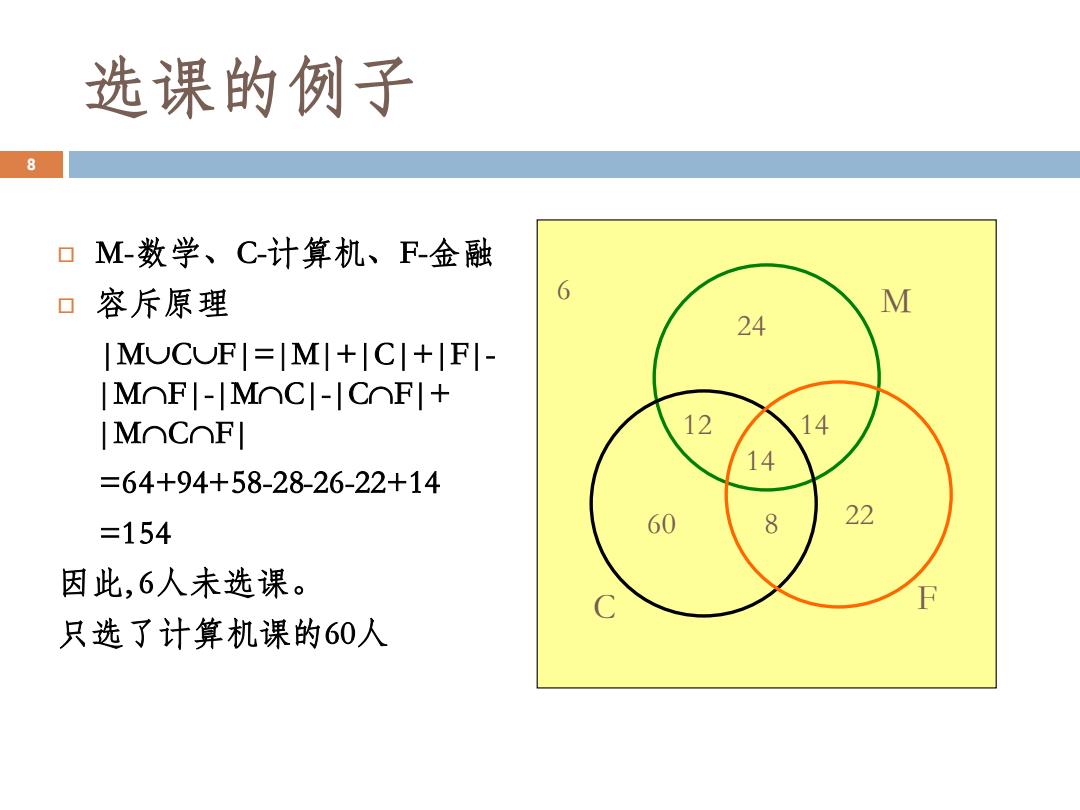
选课的例子 8  M-数学、C-计算机、F-金融  容斥原理 |MCF|=|M|+|C|+|F|- |MF|-|MC|-|CF|+ |MCF| =64+94+58-28-26-22+14 =154 因此, 6人未选课。 只选了计算机课的60人 M C F 14 12 14 8 24 60 22 6

容斥原理 (Principle of Inclusion and Exclusion) 假设A,A2,,A是个有限集合，则它们的并集的元素个数是： 0-S-8+S,+(-3++-5. 其中，S=】 ∑1A∩A,n∩A|k=1,2…,n l≤i1≤i2≤.≤ik≤n 例如：4个子集的公式为： 1A1+1A21+1A31+1A4T (A1∩A2l+|A1∩A3|+|A1∩A4|+1A2A3|+|A2A4l+|A3∩A4l) +(IA1OA2∩A3+|A1∩A2∩A4l+|A1∩A3∩A4|+|A2∩A3∩A4l) -|A1∩A2∩A3∩A4l

容斥原理 (Principle of Inclusion and Exclusion )      = =    = = + + − + + − i i i n k i i i n n k k n k k S A A A k n S S S S S A A A 1 ... -1 -1 1 2 3 n i 1 i 1 2 1 2 1 2 | ... | 1,2,..., A - -... ( 1) ... ( 1) , ,..., n 其中， 假设 是 个有限集合，则它们的并集的元素个数是：  例如：4个子集的公式为： |A1|+ |A2|+ |A3|+ |A4| - (|A1A2|+|A1A3|+|A1A4|+|A2A3|+|A2A4|+|A3A4|) + (|A1A2A3|+|A1A2A4|+|A1A3A4|+|A2A3A4|) - |A1A2A3A4|

容斥原理的证明 ▣公式：UA=S,-S2+S,-+(-1)S++(-1)Sn i=1 口我们证明并集中的元素在右边式子中恰好被计数1次 口设并集中对象a出现在m个集合A中 则它在在S中被计数m次，在S2中被计数C2”次 口 ■以n=4,m=3为例： S1:1Al+1A21+1A3l+1Al S2: -(IA1∩A2I+|A1∩A3|+|A1∩A4|+|A2∩A3|+|A2∩A4I+|A3∩A4I) S3: +(IA1∩A2∩A3+|A1∩A2∩A4|+|A1∩A3∩A4|+|A2∩A3∩A4) S4: -|A1∩A2∩A3∩A4

容斥原理的证明  公式：  我们证明并集中的元素在右边式子中恰好被计数1次  设并集中对象a出现在m个集合Ai中  则它在在S1中被计数m 次，在S2中被计数 次 ◼ 以n=4，m=3为例： n n k k S S S S S -1 -1 1 2 3 n i 1 i A = - + -...+ (−1) +...+ (−1) =  m C2 |A1|+ |A2|+ |A3|+ |A4| - (|A1A2|+|A1A3|+|A1A4|+|A2A3|+|A2A4|+|A3A4|) + (|A1A2A3|+|A1A2A4|+|A1A3A4|+|A2A3A4|) - |A1A2A3A4| S1 ： S2 ： S3 ： S4 ：

容斥原理的证明 口公式：UA=S,-S2+S-+(-1)S++(-1)Sn 口我们证明并集中的元素在右边式子中恰好被计数1次 口设并集中对象a出现在m个集合A中 则它在在S,中被计数m次，在S中被计数C次 a 口将上述分析带入计数公式可得a在右式中计数次数： Cm-C2+.+(-1)-C+.+(-1)m-Cm ■该计算式值为1，因为当x=1时下式为0： (1-x)m=1-Cmx+C2x2+.+(-1)Cx+.+(-1)C ▣a恰好被计数1次

容斥原理的证明  公式：  我们证明并集中的元素在右边式子中恰好被计数1次  设并集中对象a出现在m个集合Ai中  则它在在S1中被计数m 次，在Sk中被计数 次  将上述分析带入计数公式可得a在右式中计数次数： ◼ 该计算式值为1，因为当x=1时下式为0：  a恰好被计数1次 n n k k S S S S S -1 -1 1 2 3 n i 1 i A = - + -...+ (−1) +...+ (−1) =  m Ck m m m m k m m k C C C C 1 1 1 2 ... ( 1) ... ( 1) − − − + + − + + − m m m m k m k m m m k (1 x) 1 C x C x ... ( 1) C x ... ( 1) C x 2 − = − 1 + 2 + + − + + −