
1 集合的基数
集合的基数 1

回顾 问题1:什么是关系?如何表示关系?如何 进行关系运算? 笛卡尔积的子集;集合、矩阵、有向图;逆与复合、矩 阵法 问题2:什么是函数?什么是单射、满射函 数?如何进行函数运算? 函数是特殊的关系(所有定义域元素唯一指派);单射 满足若f(✉)=f(x),则x=x,满射满足(A)=B;反函数、 复合函数
回顾 问题1:什么是关系?如何表示关系?如何 进行关系运算? - 笛卡尔积的子集;集合、矩阵、有向图;逆与复合、矩 阵法 问题2:什么是函数?什么是单射、满射函 数?如何进行函数运算? - 函数是特殊的关系(所有定义域元素唯一指派);单射 满足若(x 1 ) =(x 2 ),则x 1 =x 2, 满射满足f(A)=B;反函数、 复合函数

本节提要 3 问题1:什么是集合的基数? 问题2:(基数)最大的集合有多大? 问题3:如何比较两个(无限)集合的大小?
本节提要 3 问题1:什么是集合的基数? 问题2:(基数)最大的集合有多大? 问题3:如何比较两个(无限)集合的大小?
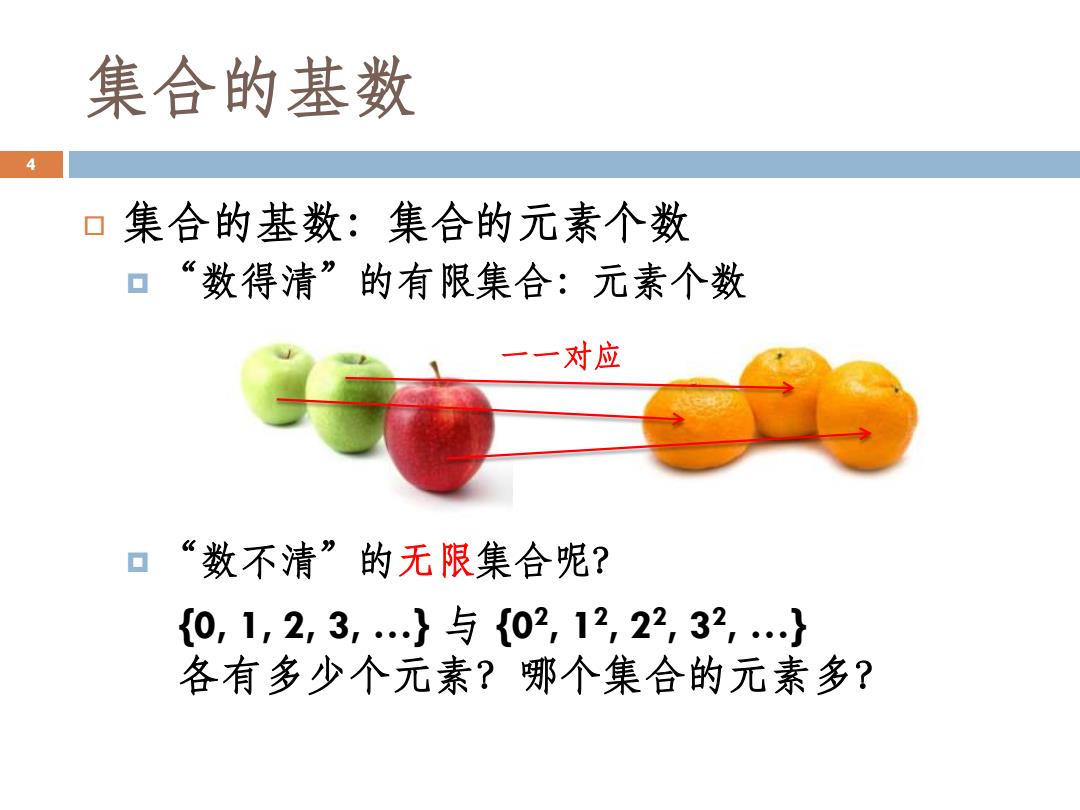
集合的基数 4 口集合的基数:集合的元素个数 口“数得清”的有限集合:元素个数 一一对应 口“数不清”的无限集合呢? 0,1,2,3,…与{02,12,22,32,…} 各有多少个元素?哪个集合的元素多?
集合的基数 集合的基数:集合的元素个数 “数得清”的有限集合:元素个数 “数不清”的无限集合呢? 4 {0, 1, 2, 3, …} 与 {0 2 , 1 2 , 2 2 , 3 2 , …} 各有多少个元素?哪个集合的元素多? 一一对应

有限与无限:“宇宙旅馆 5 啊?客满啦? 没关系,我让现 在住在k号房间 的客人移到k+1 田 号。你就住进第 1号房间吧!
有限与无限:“宇宙旅馆” 5

自然数集合的基数 6 口对于有限集合,我们用自然数描述集合的大小 口例如,苹果的个数、班级学生的个数 口那么,自然数有多少个? 口给你任意一个自然数,总有比它大的) 口定义自然数个数为X。 口读作:Aleph-null ▣父。是最小的一个无限数 )有些人依然不相信无限的存在。这门课接受无穷公理,即自然数集是无限的
自然数集合的基数 对于有限集合,我们用自然数描述集合的大小 例如,苹果的个数、班级学生的个数 那么,自然数有多少个? 给你任意一个自然数,总有比它大的(*) 定义自然数个数为ℵ0 读作:Aleph-null ℵ0是最小的一个无限数 6 (*)有些人依然不相信无限的存在。这门课接受无穷公理,即自然数集是无限的

比较集合的大小:等势关系 如果存在从集合A到B的双射,则称集合A与B等 势 口记为:A≈B,否则AB 口双射意味着:A,B中的元素可以“一一对应” 口要证明A≈B,找出一个从A到B的双射 ▣集合的势就是集合的基数,记为|A|或card A 口“等势”的集合就被认为是“一样大
比较集合的大小:等势关系 如果存在从集合A到B的双射,则称集合A与B等 势 记为:A≈B, 否则A≉B 双射意味着:A,B中的元素可以“一一对应” 要证明A≈B,找出一个从A到B的双射 集合的势就是集合的基数,记为|A| 或 card A “等势”的集合就被认为是“一样大” 7

有限集与无限集(1) 8 口S是有限集合/有穷集合,if存在自然数n,使得S 的基数为n(S与n等势) ■证明:自然数集N是无穷集 反设N有穷,从而存在n以及双射函数f:n→N,令 m=f(0)+f(1)+…+f(n-1)+1,从而有x∈ n,f(x)≠m,故f非满射,矛盾!故N为无穷集.口
有限集与无限集(1) S是有限集合/有穷集合,iff 存在自然数n,使得S 的基数为n(S与n等势) 8

有限集与无限集(2) 9 S不是有限集合(是无限集/无穷集),if存在S的 真子集S',使得S与S'等势 →S一定包含一个与自然数集合等势的子集M={a,41,42…} 令S=S-{ao},可以定义f:S→S如下: 对于任意a,∈M,fa)=a+1;对于任意x∈S-M,fx)=x 显然这是双射,即S与其真子集等势。 ∈假设S是有限集,令S=n,则对S的任意真子集S”,若S =m,必有m<1,因此从S到S的任一单射不可能是满射
有限集与无限集(2) S不是有限集合(是无限集/无穷集),iff 存在S的 真子集S’,使得S与S’等势 9

本节提要 10 问题1:什么是集合的基数? 有限集合的基数就是一个自然数,表示集合的元素个数 无限集合中最小的那一个就是自然数集合,它的基数是心。 我们也可以判断一个集合是有限还是无限 问题2:(基数)最大的集合有多大? 问题3:如何比较两个(无限)集合的大小?
本节提要 10 问题1:什么是集合的基数? - 有限集合的基数就是一个自然数,表示集合的元素个数 - 无限集合中最小的那一个就是自然数集合,它的基数是ℵ0 - 我们也可以判断一个集合是有限还是无限 问题2:(基数)最大的集合有多大? 问题3:如何比较两个(无限)集合的大小?