电子科技大学：《数学物理方程与特殊函数 Mathematical Physics Equations with Special Function》课程教学资源（课件讲稿）第八章 Legendre多项式 §8.2 母函数与正交性

§8.2母函数与正交性 一、Legendre多项式母函数 w(x,z)=∑P(x)z” Legendre多项式 n/2] P(x)=(-1)" (2n-2m)g 比n-2m =0 2"m.(n-m)(n-2m)! 制/01+ 母函数 第色 [n/2]= n/2, n为正偶数时 (n-1)/2,n为正奇数时

§8.2 母函数与正交性 一、 Legendre多项式母函数     0 ( , ) ( ) n n n w x z P x z        [ / 2] 0 2 2 !( )!( 2 )! (2 2 )! ( ) ( 1) n m n m n m n x m n m n m n m P x n 为正偶数时  n 为正奇数时     ( 1)/ 2, / 2, [ / 2] n n n Legendre多项式

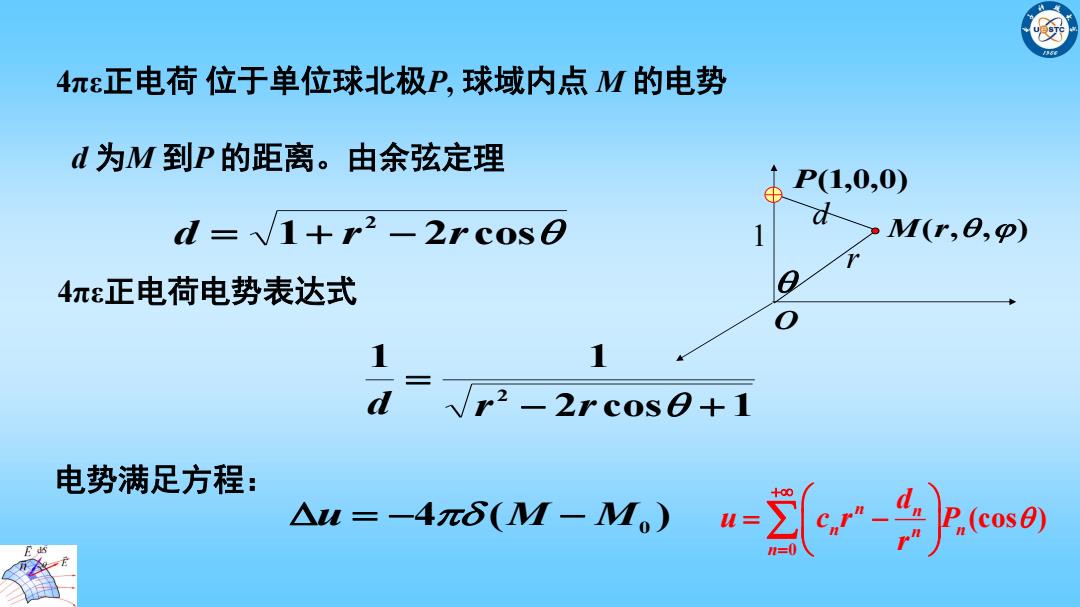
4π正电荷位于单位球北极P,球域内点M的电势 d为M到P的距离。由余弦定理 ⊕ P(1,0,0) d=1+r2-2rcose M(r,e,p) 4πε正电荷电势表达式 1-d r2-2rc0s0+1 电势满足方程： △u=-4πδ(M-M) c.(cmo

4πε正电荷 位于单位球北极P, 球域内点 M 的电势 d 为M 到P 的距离。由余弦定理 1 2 cos 2 d   r  r 4πε正电荷电势表达式 2 cos 1 1 1 2    d r r  M(r,,) O P(1,0,0)  1 r d 电势满足方程： 4 ( ) u    M  M0 0 (cos ) n n n n n n d u c r P r            

因此， r29-到.omo .(co0 令c0s0=1 -oreo-Zor 1 r2-2r+1 由 1 +00 1 得cn=1 =0 F-2g42ramove1

因此， 2 0 0 1 (cos ) 2 cos 1 (cos ), 1 n n n n n n n n n n d c r P r r r c r P r                      2 0 0 1 (1) 2 1 n n n n n n n c r P c r r r           令 cos 1   0 1 1 n n r r     由  得 1 n c  2 0 1 (cos ), 1 2 cos 1 n n n r P r r r         

取x=cos0,4πe正电荷电势表达式 .(x)r" /r2-2xr+1 n=0 取=z得 1 +00 z2-2xz+1 ∑Pn(x)z” n=0 因此，母函数为 1 w(x,z)= √V22-2xz+1

取 x  cos , 4πε正电荷电势表达式 2 0 1 ( ) 2 1 n n n P x r r xr       取 r=z 得 2 0 1 ( ) 2 1 n n n P x z z xz       因此，母函数为 2 1 ( , ) 2 1 w x z z xz   

二、Legendre多项式递推关系 =(x-z)1-2xz+z2)3/2 Oz 1-2xz+z2)a2+(z-x)w=（ w(x,z)=之Pn(x)z” =0 1-2xz+z2)2nP21+(z-x)Pz”=0 递推关系1： (n+1)P+1-(2n+1)xP+nPa-1=0 (n=1,2,…)

2 3/ 2 ( )(1 2 )        x z xz z z w (1 2 ) ( ) 0 2        z x w z w xz z     0 ( , ) ( ) n n n w x z P x z (1 2 ) ( ) 0 1 0 2 1             n n n n n n xz z nP z z x P z (n1)Pn1 (2n1)xPn  nPn1  0 (n  1, 2, ) 二、 Legendre多项式递推关系 递推关系1：

递推关系1： (n+1)Pn+1-(2n+1)xPm+nPm-1=0 (n=1,2,·…) 求导后得 (n+1)P+1-(2n+1)(xP%+Pn)+nP0-1=0

(n1)Pn1 (2n1)xPn  nPn1  0 (n  1, 2, ) (n1)Pn  1 (2n1)(xPn   Pn ) nPn  1  0 递推关系1： 求导后得

Ow Ox =z(1-2+z2) (1-2xz+z)w -2w=0 w(x,z)=∑P(x)z” ≥IPg-2xP1+P-2-P1lz”=0 P-2xP1+P1-2-Pn-1=0

2 3 2 (1 2 )       z xz z x w (1 2 ) 0 2       zw x w xz z     0 ( , ) ( ) n n n w x z P x z Pn   2xPn  1  Pn  2  Pn1  0 [ 2 ] 0 2     1   2  1       n n n n n n P xP P P z

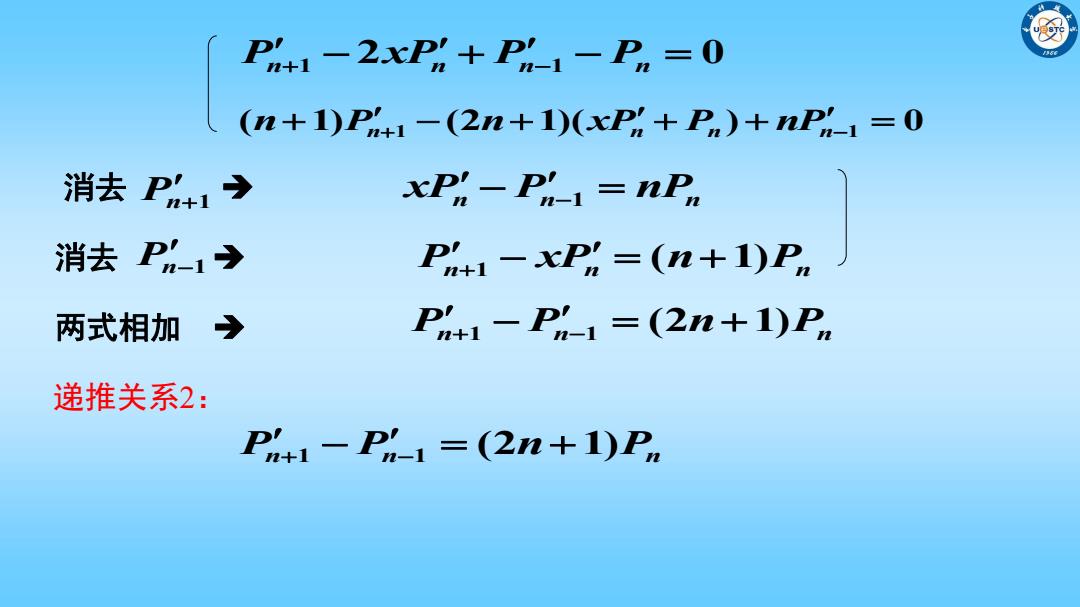
P+1-2xP+P以1-Pn=0 (n+1)P+1-(2n+1)xP%+Pn)+nP-1=0 消去P%+1→ xPr-Pi=nPu 消去P-1→ P+1-xPw=(n+1)P。 两式相加 P+1-P-1=(2n+1)Pn 递推关系2： P+1-P-1=(2n+1)Pn

(n1)Pn  1 (2n1)(xPn   Pn ) nPn  1  0 Pn  1  2xPn   Pn  1  Pn  0 xPn Pn  nPn    消去 1 Pn  1  消去 Pn  1  Pn xPn n Pn ( 1)  1     两式相加  Pn Pn n Pn (2 1)  1   1   递推关系2： Pn Pn n Pn (2 1)  1   1  

三、Legendre多项式正交性 J.(eP(e=0,(m≠四 证：由Legendre7方程 (1-x2)Pw"-2xPm+(n+1)Pn=0 [(1-x2)P'+n(n+1)Pn=0 P(x)x [1-x2)P%'+n(n+1)Pn=0 Pn(x)×1 [(1-x2)PI'+m(m+1)P=0 P[(1-x2)P+n(n+1)PP=0 P[(1-x2)P'+m(m+1)P Pn =0

三、Legendre多项式正交性 ( ) ( ) 0, ( ) 1 1 Pn x Pm x dx  m  n  Pn (x) Pm (x)  (1 ) 2 ( 1) 0 2  x Pn  xPn   n n Pn  证: 由Legendre方程 [(1 ) ] ( 1) 0 2  x Pn    n n Pn  [(1 ) ] ( 1) 0 2  x Pn    n n Pn  [(1 ) ] ( 1) 0 2  x Pm    m m  Pm  [(1 ) ] ( 1) 0 2 Pm  x Pn    n n Pm Pn  [(1 ) ] ( 1) 0 2 Pn  x Pm    m m  Pn Pm 

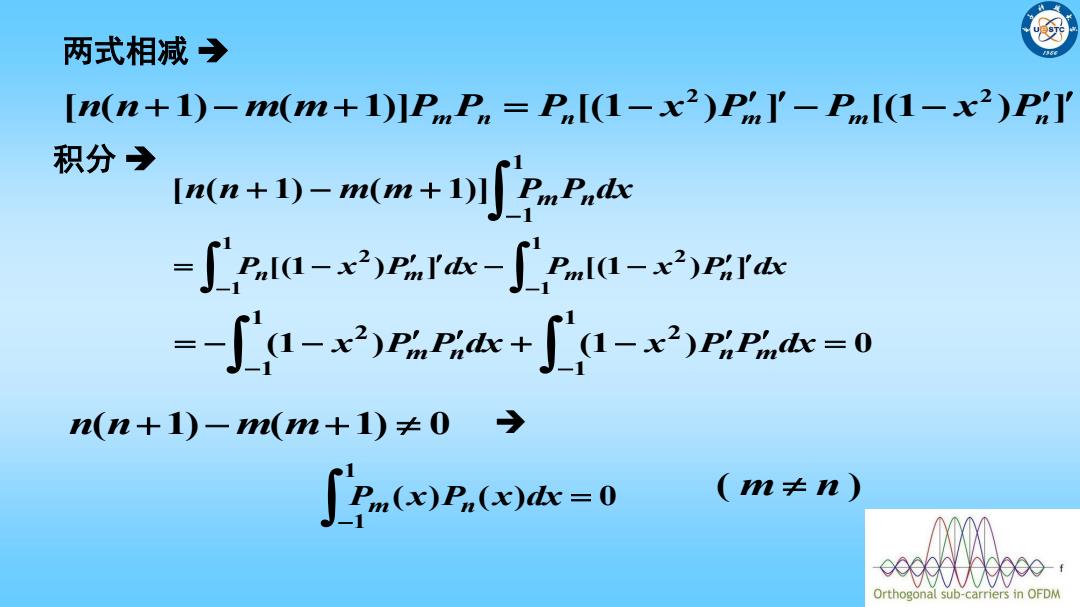
两式相减 [n(n+1)-m(m+1]PP=P[(1-x2)PI'-Pr(1-x2)P:l 积分→ Ln(n+1)-m(m+1ds =∫P.la-x2Pr-∫PI-2r& =-∫1-x2)PPk+4-x2)P以P=0 n(n+1)-n(n+1)≠0→ Sr()(d=0 (n≠n) 9900e: Orthogonal sub-carriers in OFDM

两式相减  [ ( 1) ( 1)] [(1 ) ] [(1 ) ] 2 2            n n m m Pm Pn Pn x Pm Pm x Pn 积分      1 1 [n(n 1) m(m 1)] Pm Pndx           1 1 2 1 1 2 Pn [(1 x )Pm] dx Pm[(1 x )Pn ] dx (1 ) (1 ) 0 1 1 2 1 1 2             x Pm Pn dx x Pn Pmdx n(n1) m(m1)  0  ( ) ( ) 0 1 1   Pm x Pn x dx ( m  n )