
§5.2 Fourier?变换应用 例一根半无限长的杆,初始温度分布等于零,且在端点=0处热流密度为 h(d,求杆的温度分布。 解: 4,=a24c,x∈(0,+o∞),t>0 u(x,0)=0 ,0,0=-)=g0 用余弦变换求解,令 u(o,t)=F(u(x,t))
§5.2 Fourier变换应用 例 一根半无限长的杆,初始温度分布等于零,且在端点x=0 处热流密度为 h(t) ,求杆的温度分布。 解: ( , ) ( ( , )) u t F u x t c c 用余弦变换求解, 令 2 , (0, ), 0 ( ,0) 0 1 (0, ) ( ) ( ) t xx x u a u x t u x u t h t g t k x O
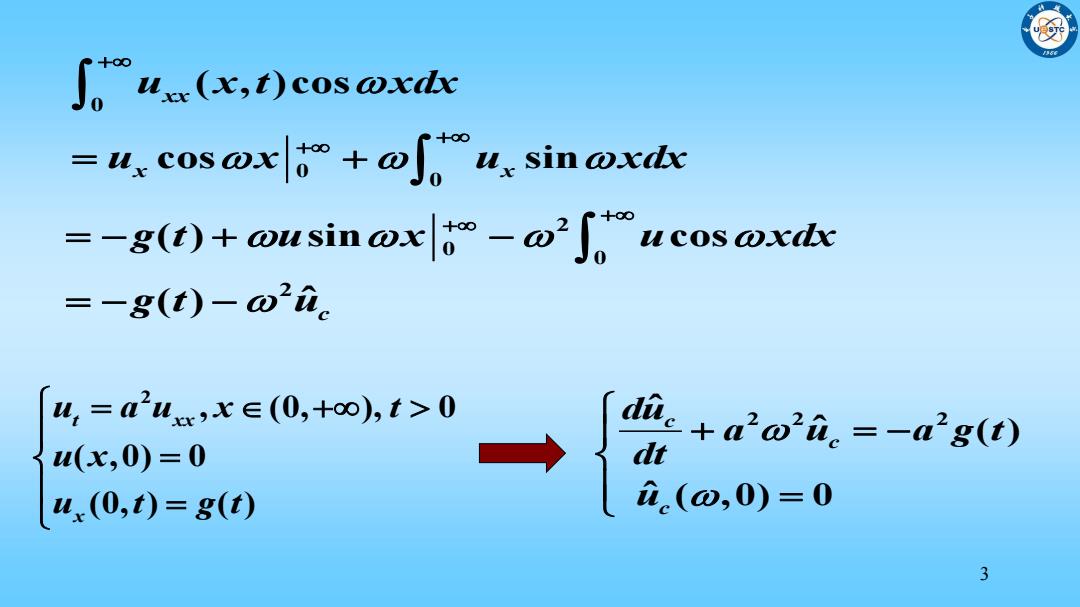
u()cos@xdx -ux cosox+ofus sin oxdx --g(t)+ousin@x-@fucos@xdx =-8(t)-o2i ,=2ux,x∈(0,+oo),t>0 u(x,0)=0 dic +a'o'i =-a'g(t) dt u(0,t)=g(t) i(w,0)=0 3
3 2 2 2 ˆ ˆ ( ) ˆ ( ,0) 0 c c c du a u a g t dt u 0 0 0 ( , )cos cos sin xx x x u x t xdx u x u xdx 2 , (0, ), 0 ( ,0) 0 (0, ) ( ) t xx x u a u x t u x u t g t 2 0 0 2 ( ) sin cos ( ) ˆ c g t u x u xdx g t u
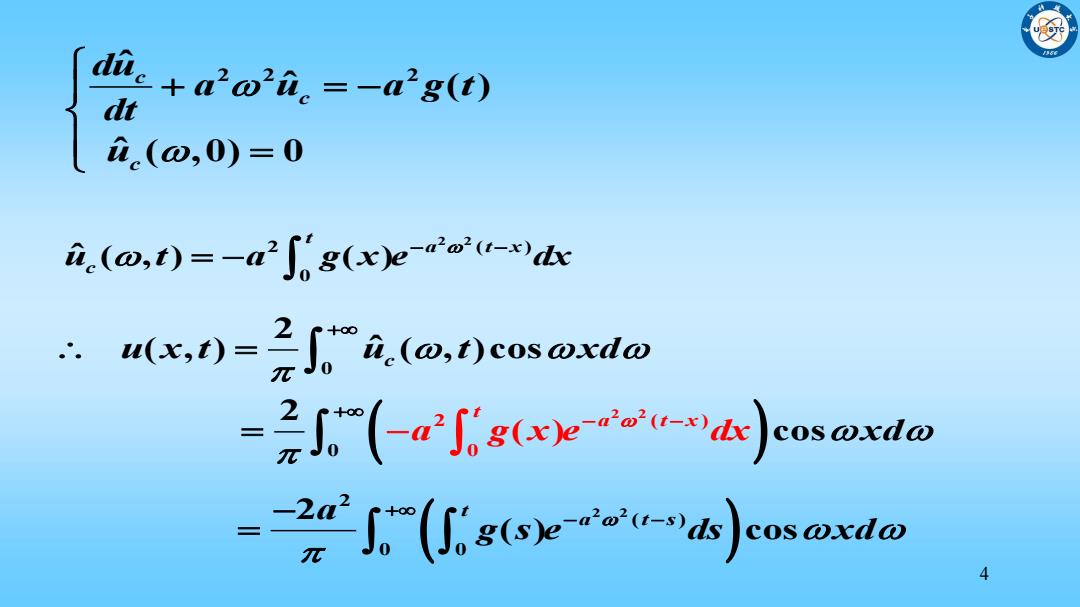
+2o2a.=-dg(0 dt i.(o,0)=0 i(@,t)=-a25g(x)e-ndx x.()cosoxdo ()cosxd = =(g(sy--b小cusoxdw 4
4 2 2 2 ˆ ˆ ( ) ˆ ( ,0) 0 c c c du a u a g t dt u 2 2 2 ( ) 0 ˆ ( , ) ( ) t a t x u t a g x e dx c 2 2 0 2 ( ) 0 0 2 ( , ) ( , )cos ˆ 2 cos ( ) c t a t x u x t u a g x e d t x x x d d 2 2 2 ( ) 0 0 2 ( ) cos t a a t s g s e ds xd

-2j(gseo-k)osom =-w6w(2。w-Dcoswxda)k =20geak 2 2元 e-a cos @xd@= 时间 t元 6000 200
5 2 2 2 2 2 ( ) 0 0 2 ( 0 ) 0 2 co 2 ( ) cos ( ) s a t s t a t s t e a g s e ds xd a s s g d xd 2 2 2 2 4 0 2 1 cos x a t a t e xd e a t 2 2 4 ( ) 0 1 ( ) x t a a t s g s e ds t s