电子科技大学：《数学物理方程与特殊函数 Mathematical Physics Equations with Special Function》课程教学资源（课件讲稿）第八章 Legendre多项式 §8.1 Legendre方程与求解

激学物理方程与特殊函激精品课程 第八章Legendre.多项式 主讲：李明奇副教授

主讲：李明奇 副教授 第八章 Legendre多项式

HYDROGEN §8.1 Legendre方程与求解 PROTON 一、Schrodinger方程 ELECTON ih平c,0=2 V2+V()Ψ(f,t) at ●普朗克常数 h=6.6260755×10-34J5 h=h/2元 Ze' V()=-

§8.1 Legendre方程与求解 一、 Schrödinger方程 普朗克常数 ( )] ( , ) 2 ( , ) [ 2 2 r t V r r t t i               h Js 3 4 6.6260755 10     h/ 2 r Ze V r 2 ( )   

Schrodinger7方程 aΨ at 2 分离变量：设(x,y,,t)=w(x,y,)f(t) →定态Schrodinger?方程 v-Zw-EV 2 若令 i=，则 2u Ay=Ev

3 Schrödinger方程        ] 2 [ 2 2 2 r Ze t i       E r Ze    )  2 ( 2 2 2  定态Schrödinger方程 分离变量: 设 (x, y,z,t) (x, y,z) f (t) r Ze H 2 2 2 2 ˆ       若令 ，则 H ˆ   E

势能具球面对称性，考虑坐标变换 x=rsinecoso y=rsinesing z=rcose y P a2y业+ay +02 0≤p≤2π，0≤8≤π 1∂ V'w= 2∂y 1 1 8'w 2 00r2 sin'edo 8c+ ze2 4r2 其中 2=-h1.1 162 sin0 00 sin2002

  r r  y x z      cos sin sin sin cos z r y r x r     0   2, 0              2 2 2 2 2 2 2 x y z     2 2 2 2 2 2 2 2 sin 1 (sin ) sin 1 ( ) 1                         r r r r r r 势能具球面对称性, 考虑坐标变换 r ze r L r r r r H 2 2 2 2 2 2 2 ˆ ( ) 1 2 ˆ             ] sin 1 (sin ) sin 1 [ ˆ 2 2 2 2 2              其中 L  

球坐标系下定态Schrodinger方程 人 分离变量法，设 v(r,0,p)=R(r)Y(0,o)

    E r Ze r L r r r r         ] 2 ˆ ( ) 1 2 [ 2 2 2 2 2 2  球坐标系下定态Schrödinger方程 分离变量法, 设 (r,,)  R(r)Y(,) ] ( ) 2 ˆ ( ) 2 [ 2 2 2 2 2 2 RY E RY r L r Ze r r r r            

→R)满足径向方程： )+2 dr dr +R=1u+1)R →Y(O,p)满足角向方程： 1y=1(1+1)Y ∂ 1 a'y sine a0 sin680+io8++nr=0 再次分离变量，设 Y(B,p)=⊙(B)Φ(p)

 R(r) 满足径向方程： R l l R r Z e E r d r d R r d r d [ ] ( 1) 2 ( ) 2 2 2 2       L ˆ Y l(l 1)Y 1 2 2     Y(, ) 满足角向方程： ( 1) 0 sin 1 (sin ) sin 1 2 2 2           l l Y Y Y       再次分离变量, 设 Y(,)  ( )()

d2Φ ①(p)满足经度方程： +九Φ=0 x=cos ⊙(0)满足纬度方程： 0 1 d2⊙ )cos e d⊙ 0<B<元 de2 sine de ++)- sin2al-0 一1<x<1 引入变量x=c0s8 3-装-2 ++-m=0 dx

0 2 2      d d  ( ) 满足经度方程：  ( ) 满足纬度方程： ] 0 sin [ ( 1) sin cos 2 2 2 2              m l l d d d d 引入变量 x  cos x  cos 0    1 x  1 ] 0 1 (1 ) 2 [ ( 1) 2 2 2 2 2        y x m l l dx dy x dx d y  x

a--2++-少-0 dx 连带Legendre方程.取t=0,Legendre方程： a-x2)4g-2x+1+y=0 dx2 dx 设Legendre方程解可表示为幂级数形式 y=x(an+a,x+a2x2++anx”+）=∑44x+d dx 1752~1833

] 0 1 (1 ) 2 [ ( 1) 2 2 2 2 2        y x m l l dx dy x dx d y x 连带Legendre方程. 取 m=0,  Legendre方程： (1 ) 2 ( 1) 0 2 2 2    l l  y  dx dy x dx d y x 设Legendre方程解可表示为幂级数形式      1 1 k k kak x dx dy 2 0 2 0 1 ( ) k c n k k c n y a x x a a x a x a x            1752~1833

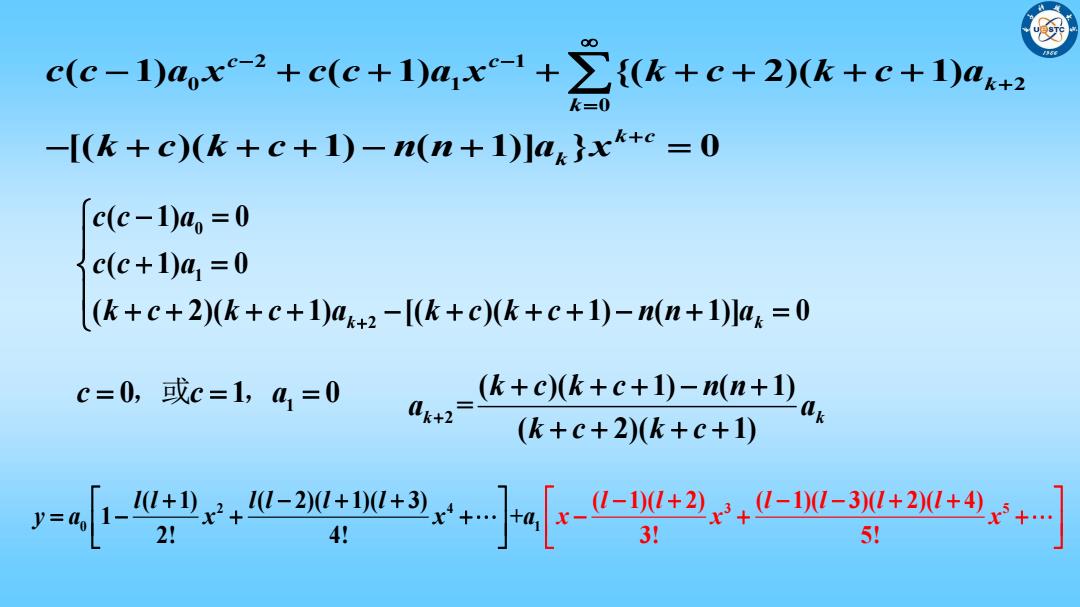
c(c-1)ax-2+c(c+1)a,x1+∑(k+c+2)(k+c+1)ak+2 k=0 -I(k+c)(k+c+1)-n(n+1)ak}xk+c=0 c(c-1)a=0 c(c+1)a1=0 (k+c+2)(k+c+1)ak+2-(k+c)k+c+1)-(n+Ias=0 c=0,或c=1,41=0 a-+ck+c+)-u+) (k+c+2)(k+c+1) y=-[-e+-2nr+[k-2,-W-2w+e+ 5!

0 1 2 ( 1) 0 ( 1) 0 ( 2)( 1) [( )( 1) ( 1)] 0 k k c c a c c a k c k c a k c k c n n a                      2 1 0 1 2 0 ( 1) ( 1) {( 2)( 1) [( )( 1) ( 1)] } 0 c c k k k c k c c a x c c a x k c k c a k c k c n n a x                       1 c c a    0 1 0 ，或 ， 2 ( )( 1) ( 1) = ( 2)( 1) k k k c k c n n a a k c k c           2 5 0 1 4 3 ( 1) ( 2)( 1)( 3) 1 + 2! 4 ( 1)( 2) ( 1)( 3)( 2)( 4) ! 3! 5! l l l l l l x l l l l l l y a x x a x x                             

y=a,1-1+Dx2+-2u+1)0+3)x4+ 2} 4: ,=4,Ix--L+2)x3+=0-3+2+4)x+ 3 5! Legendre方程幂级数解 y=y1(x)+y2(x) 当1为正偶数时，y1c)为多项式，y2)为无穷级数 当1为正奇数时，y2心)为多项式，y1(x)为无穷级数 以n替换I,重新整理Legendre方程多项式系数 (21n)g_1.3.5…(2n-1 n= 2"(n)2 n! 2,n-1,n-2,n-3

Legendre方程幂级数解 ] 4! ( 2)( 1)( 3) 2! ( 1) [1 2 4 1 0         x l l l l x l l y a ] 5! ( 1)( 3)( 2)( 4) 3! ( 1)( 2) [ 3 5 2 1           x l l l l x l l y a x ( ) ( ) y  y1 x  y2 x 当 l 为正偶数时, y1 (x)为多项式, y2 (x) 为无穷级数 当 l 为正奇数时, y2 (x)为多项式, y1 (x) 为无穷级数 以 n 替换 l , 重新整理Legendre方程多项式系数 2 (2 )! 1 3 5 (2 1), 1, 2, 3, 2 ( !) ! n n n n a n n n n n          