电子科技大学：《数学物理方程与特殊函数 Mathematical Physics Equations with Special Function》课程教学资源（课件讲稿）第五章 积分变换 5.2 Fourier变换应用（2/3）

§5.2 Fourier?变换应用 例设有一根无限长的杆，杆上有强度为F化，)的热源，杆的初始温度为 px)，试求>0时杆上温度的分布规律。 解： x x+dx ∂w =a20+f(x,,(-o0 8t =p(x) f(x)=IF(.t) i(@,t)=u(x,t)e-iodx, f(o,t)=∫f(x,t)eiok

§5.2 Fourier变换应用 例 设有一根无限长的杆，杆上有强度为F(x, t) 的热源，杆的初始温度为 φ(x) ，试求 t>0 时杆上温度的分布规律。 解：   2 2 2 0 ( , ), , 0 ( ) t u u a f x t x t t x u x                   1 f x t F x t ( , ) ( , ) c  j j ˆ( , ) ( , ) , ˆ ( , ) ( , ) x x u t u x t e dx f t f x t e dx               x x+dx x

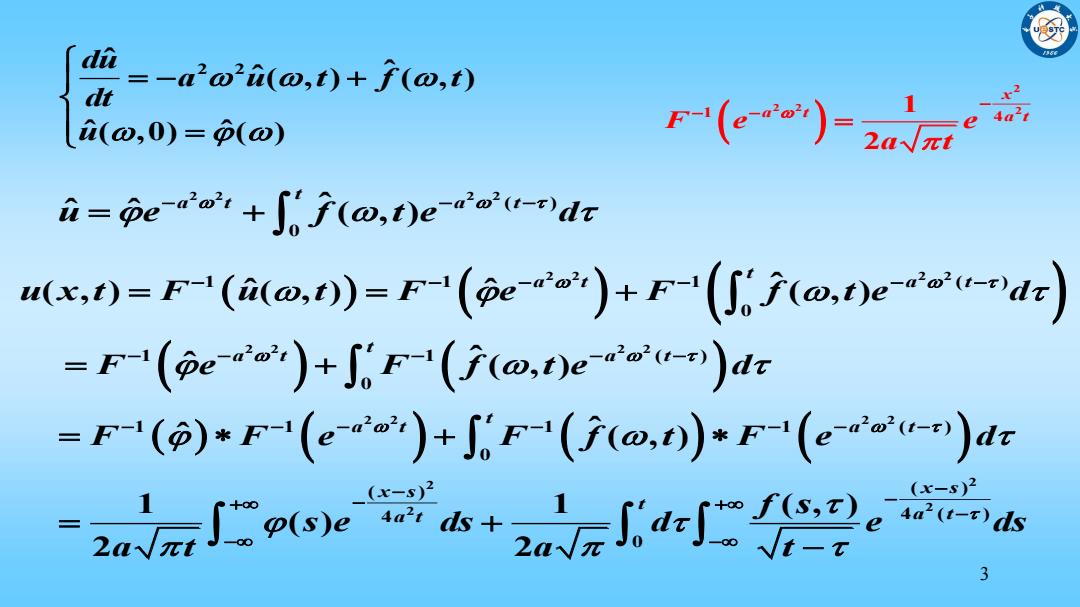
di dt --a2@2i(@,t)+j(@,t) i(o,0)=p(o) i=pe-w,+5F(@,t)e-aou-dr M,=F(aom.0)=k(ea）+F'(g7o,eu-ndr） =F-'(De）+J6F-'(f(o,)eou-）tc =F(@)*F-'(eo）+jF'(f@,）*F-(eou-）ur (x-s)2 n∫(oek+ad 3

3 2 2 ˆ ˆ ˆ( , ) ( , ) ˆ( ,0) ( ) ˆ du a u t f t dt u                2 2 2 2 ( ) 0 ˆ ˆ ˆ ( , ) t a t a t u e f t e d               2 2 2 1 2 4 1 2 x F e e a t a t a t             2 2 2 2 1 1 1 ( ) 0 ˆ ( , ) ( , ) ( , ) ˆ ˆ t a t a t u x t F u t F e F f t e d                      2 2 2 2 1 1 ( ) 0 ˆ ˆ ( , ) t a t a t F e F f t e d                       2 2 2 2 2 2 2 2 1 1 1 1 ( ) 0 ( ) ( ) 4 4 ( ) 0 ˆ ˆ ( , ) 1 1 ( , ) ( ) 2 2 t a t a t x s x s t a t a t F F e F f t F e d f s s e ds d e ds a t a t                                        

例求半无界杆的热传导问题 Ou =a 8t ax2,(00) ux-0=Ho u=0=0 解：将边界条件齐次化，仿照半无界弦的波动问题作奇延拓，将问题化为无界问题 u(x,t)=w(x,t)+u Ow =2w】 Ot a2,(00) w x=0=0 w|=0=一0 4

4 例 求半无界杆的热传导问题   2 2 2 0 0 0 , 0 , 0 0 x t u u a x t t x u u u                    解：将边界条件齐次化，仿照半无界弦的波动问题作奇延拓，将问题化为无界问题 0 u x t w x t u ( , ) ( , )     2 2 2 0 0 0 , 0 , 0 x 0 t w w a x t t x w w u                    

Ou Ot g+fx,,(-0 0) 的解为 u(x,0)=p(x) u(x,t)=F(i(@,t)) _(x-s)2 -(x-s)2 2avpea 本题 e,=2w,(00) w(x,0)=-uo w(0,t)=0 5

5   2 2 2 ( , ), , 0 ( ,0) ( ) u u a f x t x t t x u x x                  2 2 2 2 1 ( ) ( ) 4 4 ( ) 0 ( , ) ( ( , )) ˆ 1 1 ( , ) ( ) 2 2 x s x s t a t a t u x t F u t f s s e ds d e ds a t a t                          的解为 2 0 ,(0 , 0) ( ,0) (0, ) 0 w a w x t t xx w x u w t              本题

本题中f(x,t)=0 _(x-s)2 (x)=aape, ∈R 2 u0.0)=2aJro(sek=0 p(x)作奇延拓 w,-a2w=0,(-∞0) la-pw-{rco9》 6

6 本题中 f x t ( , ) 0  2 2 ( ) 4 1 ( , ) ( ) , 2 x s u x t s e ds x R a t a t          2 2 4 1 (0, ) ( ) 0 2 s u t s e ds a t a t         ( ) x 作奇延拓 2 0 0 0 0,( , 0) ,( 0) ( ) ,( 0) t xx t w a w x t u x w x u x                     

w,-a2we=0,(-o0) .con 利用上题结果 u(x,t)=i+(x,t) (x-s)2 x-s)2 2 2 =u+ -小。as Mo 2 、2 =+ 7

7 2 0 0 0 0,( , 0) ,( 0) ( ) ,( 0) t xx t w a w x t u x w x u x                      利用上题结果 2 2 2 2 0 0 0 4 4 0 0 ( , ) ( , ) 2 x s x s a t a t u x t u w x t u u e ds e ds a t                       （ ） （ ） 2 2 2 2 0 4 4 0 e d e d 2 π s s a t a t x x u u s s a t                   2 2 2 2 0 4 4 0 e d e d 2 π s s x a t a t x u u s s a t                   

以n-w*2r.-小。a 2 =ia=品。品） 了2 =h 〔a小.o0, 〔-a成aeas 8

8 2 2 2 2 0 4 4 0 ( , ) e d e d 2 π s s a t a t x x u u x t u s s a t                   2 2 2 2 0 4 4 0 0 0 0 1 e d 1 e d π π s s x x a t a t u u s u s a t a t                 2 2 0 0 1 1 e d 2 π 2 s a x t s a t a t u a t                  2 2 0 0 1 e d π 2 s x a t u s          

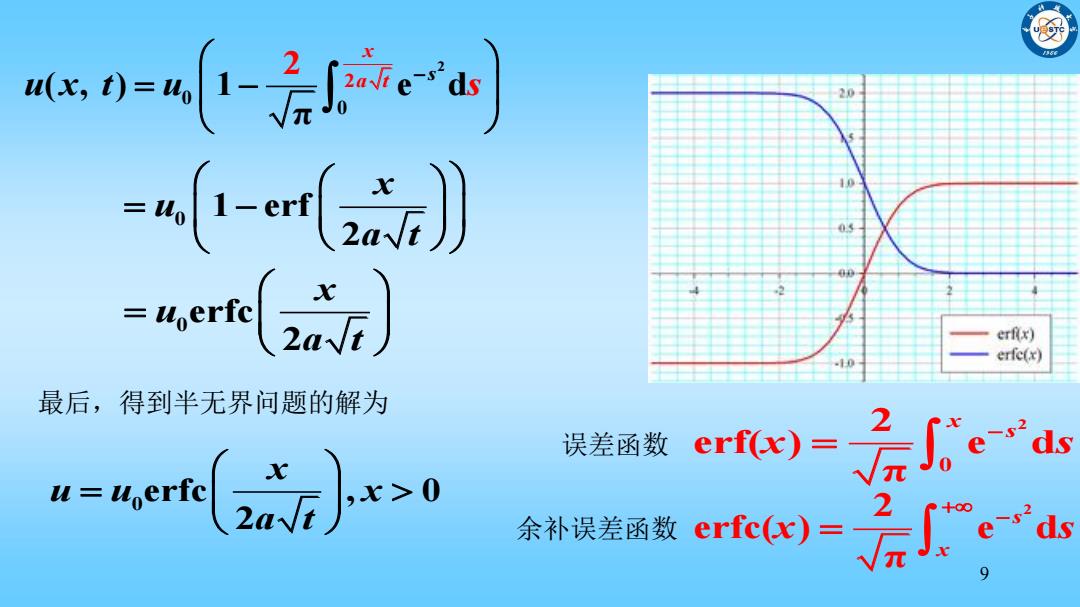
,W=n1-2e） =i-enaa)》 werts erf(x) erfe(x) 最后，得到半无界问题的解为 2 误差函数erfx)= u=ue(2}>0 Je 金数ctc)=。 2

9 2 0 2 erf( ) e d π x s x s    2 0 2 0 ( , ) 1 e d π 2 s x u x t u a t s           0 1 erf 2 x u a t               0 erfc 2 x u a t        余补误差函数 2 2 erfc( ) e d π s x x s     误差函数 最后，得到半无界问题的解为 0 erfc , 0 2 x u u x a t        