电子科技大学：《数学物理方程与特殊函数 Mathematical Physics Equations with Special Function》课程教学资源（课件讲稿）第七章 Bessel函数 §7.3 Bessel函数的正交性

§7.3 Bessel函数的正交性 一、正交性定理 定理1 Besseli函数系 (发m=2N 具有正交性： ((袋 Bessel Functions of the First Kind lo(x) 0.8 (x) 0,(m≠k) =3R2J,0)=Rm=k 0.2 0 -02 -0.4 -0.6 0 10 12 14 161820

§7.3 Bessel函数的正交性 2 一、正交性定理 定理1 Bessel函数系 ( ) 1, 2, , n m J r m n N n R                    ： 具有正交性： 2 2 ( ) 2 2 ( ) 1 0 ( ) 1 ( ) 0, ( ) 1 1 ( ) ( ) d , 2 2 n n m k n n n n m R nm n m rJ r k R J R J m J R k r r R                            

证明： d2F dF dr2 +r +(2r2-n2)F=0 dr x=√冗r dF d2+ +(x2-n2)F=0 dx F(x)=J.(x)=J(r).nEN √瓦=wm/R,(m=1,2,) TAMATHEMATICA (贤小*袋-r0 Friedrich Wilhelm 7446 (袋小m12小 1KKHU5

3 证明： 2 2 2 2 2 ( ) 0 d F dF x x x n F dx dx     2 2 2 2 2 ( ) 0 d F dF r r r n F dr dr      x r   F x J x J r n N ( ) ,    n n      2 ( ( 2 2 ) 2 ) 2 ( ) , 0 n m n n m d F dF F r J r r r n F R dr dr R r                          ( ) / ,( 1,2, ) n     m R m ( ) 1, 2, nm J r n m R               ：

些-《小一w答小 -J-0 F(x)=J (ar) ]发)-w-a 10 h d]+[r-]so=0 610 h

4 2 ( ) 2 1 1 2 2 2 2 d d ( ) ( ) 0, d d d d ( ) ( ) 0 d d n F r m n r r F r r r R r F r n r a r F r r r r                                      2 2 ( ) 2 2 2 0 n d F dF m r r r n F dr dr R            ( ) 1( ) n m F x J r n R         2 2 2 2 2 2 0 d F dF r r a r n F dr dr           2 ( ) F x J ar  n

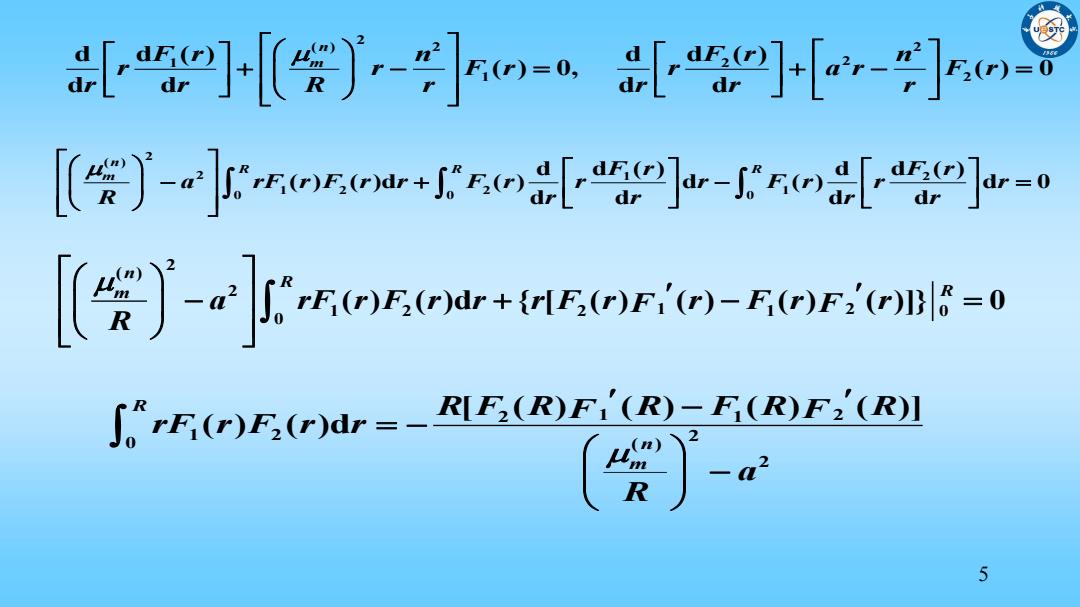
]-发)-o-w0]-[er-]o 鉴-a]oroar+ro6]ar-roaar-0 [发j-a]Foo+nrin-nko5-0 ∫rFr)Er)dr=- RIE(R)F(R)-(R)E2(R) -a2 5

5 2 ( ) 2 2 1 2 2 1 2 d d d ( ) d ( ) ( ) 0, ( ) 0 d d d d n F r F r m n n r r F r r a r F r r r R r r r r                                        2 ( ) 2 1 2 1 2 2 1 0 0 0 d d d ( ) d ( ) ( ) ( )d ( ) d ( ) d 0 d d d d n R R R m F r F r a rF r F r r F r r r F r r r R r r r r                                   2 ( ) 2 1 2 2 1 0 1 2 0 ( ) ( )d { [ ( ) ( ) ( ) ( )]} 0 n R m R a rF r F r r r F r r F r r F F R                       2 1 1 2 1 2 2 0 ( ) 2 [ ( ) ( ) ( ) ( )] ( ) ( )d R n m R F R R F R R F F rF r F r r a R              

r得"得 RE(R)FR) 广（货小-ia-r -2a xJ (x)+n.J(x)=xJ(x),xJ (x)-nJ (x)=-xJ1(x) w(gjar=空)-空uey 6

6 ( ) 2 1 2 0 ( ) 2 ( ) ( ) ( )d n R m n n n m RF R F R rJ r J ar r R a R                    ( ) ( ) 2 ( ) 2 ( ) ( ) n n m n m n n m J aR J a R              ( ) ( ) ( ) ( ) 2 0 ( ) ( ) d lim 2 n m n n n R m m m n n n a R J J aR R rJ r r R a                   2 ( ) 2 [ ( )] 2 n n m R  J   1 1 ( ) ( ) ( ), ( ) ( ) ( ) xJ x nJ x xJ x xJ x nJ x xJ x n n n n n n          ( ) 2 2 2 ( ) 1 2 ( 0 2 ) 1( ) 2 d ( ) 2 n n n m n m n R m n rJ r r R J R J R              

二、函数展开定理 定义1定积分 的平方根，称为Bessel函数 的模值。 定理2若fx)和fx)的导函数在区间[0，R至多有有限个跳跃型间断点，则fx)在区间 (0,R)内在连续点处的Bessel/展开级数收敛于该点的函数值，在间断点收敛于该 点左右极限的平均值： -玄（发小 F.Oberhettinger Tables of Bessel Transforms 《-gieu(份业

7 定义1 定积分 2 ( ) 0 1 d R n n m rJ r r R         的平方根，称为Bessel函数 1 ( ) n n m J r R        的模值。 定理2 若f(x)和f(x)的导函数在区间[0, R]至多有有限个跳跃型间断点，则f(x)在区间 （0, R）内在连续点处的Bessel展开级数收敛于该点的函数值，在间断点收敛于该 点左右极限的平均值： ( ) 1 ( ) n m m n m f r A J r R            ( ) 2 0 2 ( ) 1 1 ( ) d ( ) 2 n R k k n n n k A rf r J r r R R J            二、函数展开定理