
§5.4 Laplace变换应用 例求解半无界弦的强迫振动定解问题: 4n=a24e+cos@t,,(00) 4k=0=0,4xx→to=0 u=o=0,4,==0 解:关于自变量t作Laplace变换 L(u)=a2L(uss)+L(cos@t) L(4l=)=0,L(u.k)=0
§5.4 Laplace变换应用 2 例 求解半无界弦的强迫振动定解问题: 2 0 0 0 cos ,(0 , 0) 0, 0 0, 0 tt xx x x x t t t u a u t x t u u u u 解:关于自变量 t 作Laplace变换 2 0 ( ) ( ) (cos ) 0, 0 tt xx x x x L u a L u L t L u L u

L(u)=a2L(u)+L(cos@t) L(ul)=0.L(u)=0 40=0,4,k-0=0 sa=e da dx2 2+s2 =0,iix x=0 a2da -s2= dx2 02+s 通解(x,s)=Aea+Bea+ s(o2+s2) 3
3 2 2 2 2 2 2 x x x 0 0, 0 d u s s u a dx s u u 2 0 ( ) ( ) (cos ) 0, 0 tt xx x x x L u a L u L t L u L u u u t t t 0 0 0, 0 2 2 2 2 2 2 d u s a s u dx s 2 2 1 ( , ) ( ) s s x x a a u x s Ae Be s s 通解
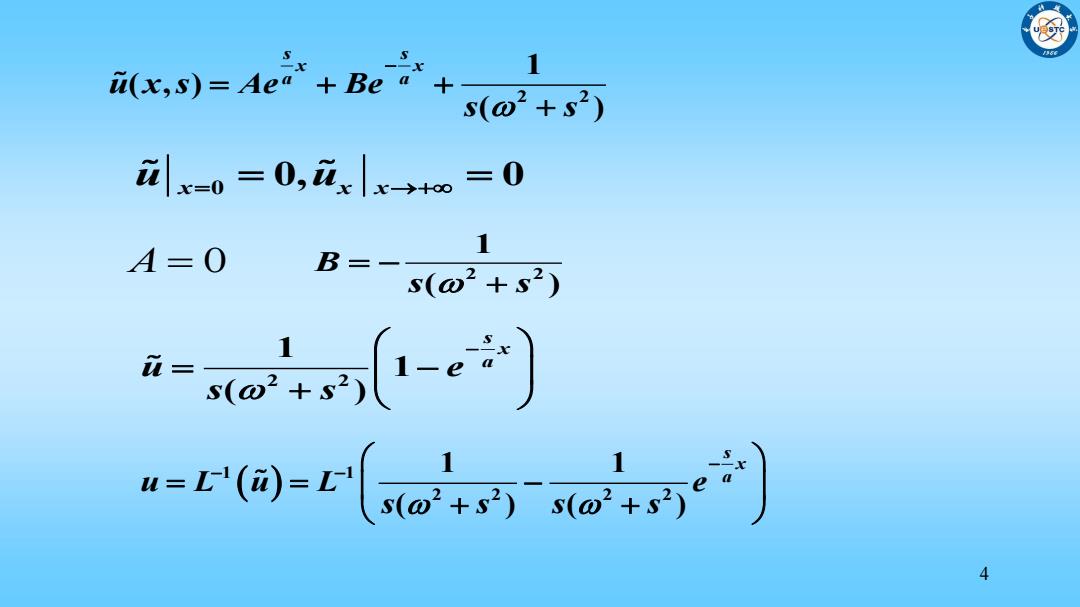
i(x,s)=Ae"+Be s(D2+s2) x=0=0,ix|x→to=0 A=0 1 B=-s(w2+s) i-ot1-e) 4
4 A 0 2 2 1 ( ) B s s 2 2 1 1 ( ) s x u e a s s 2 2 1 ( , ) ( ) s s x x a a u x s Ae Be s s u u x x x 0 0, 0 1 1 2 2 2 2 1 1 ( ) ( ) s x a u L u L e s s s s
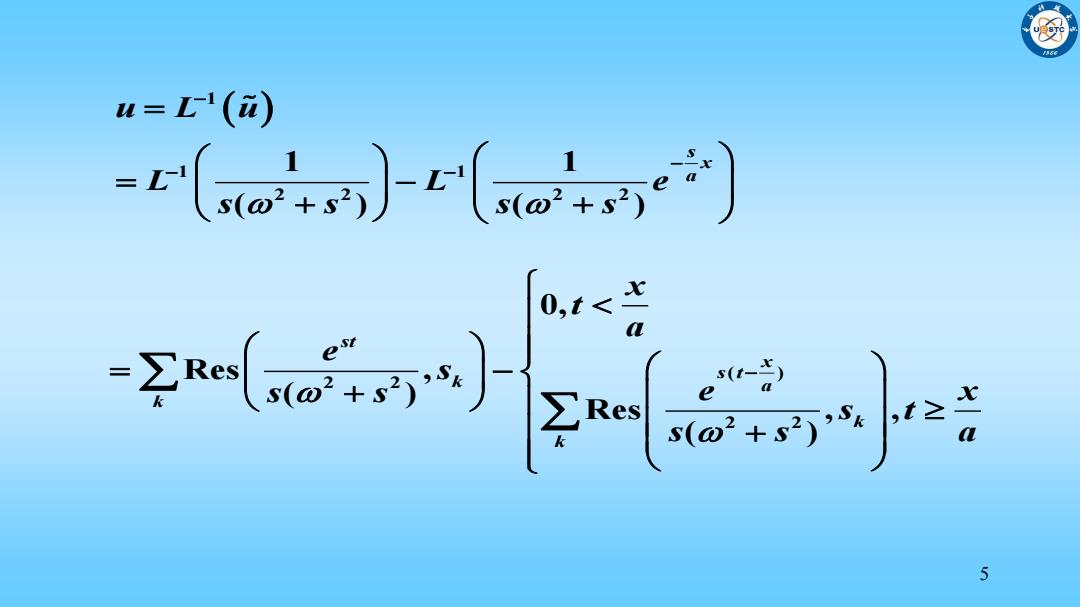
u=Li) =r(o+】r(o+e) 0,t< go ,t≥ 5
5 ( ) 2 2 2 2 0, Res , ( ) Res , , ( ) st x s t k a k k k x t a e s s s e x s t s s a 1 1 1 2 2 2 2 1 1 ( ) ( ) s x a u L u L L e s s s s
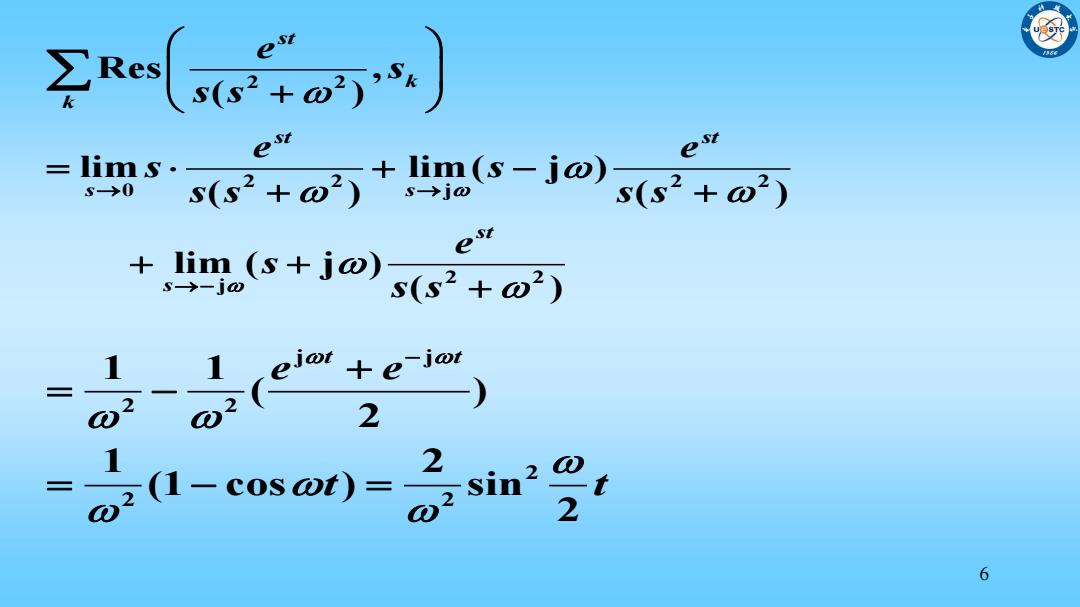
es x( e 用s(s2+o+ims-j0 =lims. s(2+o2) +1。(s+jo)ss2+m2 s→-jw 2 ee-jor 2 1 (1-cosot)=2 sin2 2 6
6 2 2 2 2 2 2 0 j 2 2 j Res , ( ) lim lim( j ) ( ) ( ) lim ( j ) ( ) st k k st st s s st s e s s s e e s s s s s s e s s s j j 2 2 2 2 2 1 1 ( ) 2 1 2 (1 cos ) sin 2 t t e e t t

若 t> ∑Res -…-】 忌n(-) 7
7 x t a j j 2 2 2 2 1 1 Res , ( ) 2 x x x s t t t a a a k k e e e s s s 2 2 2 1 1 cos 2 sin 2 x t a x t a 若
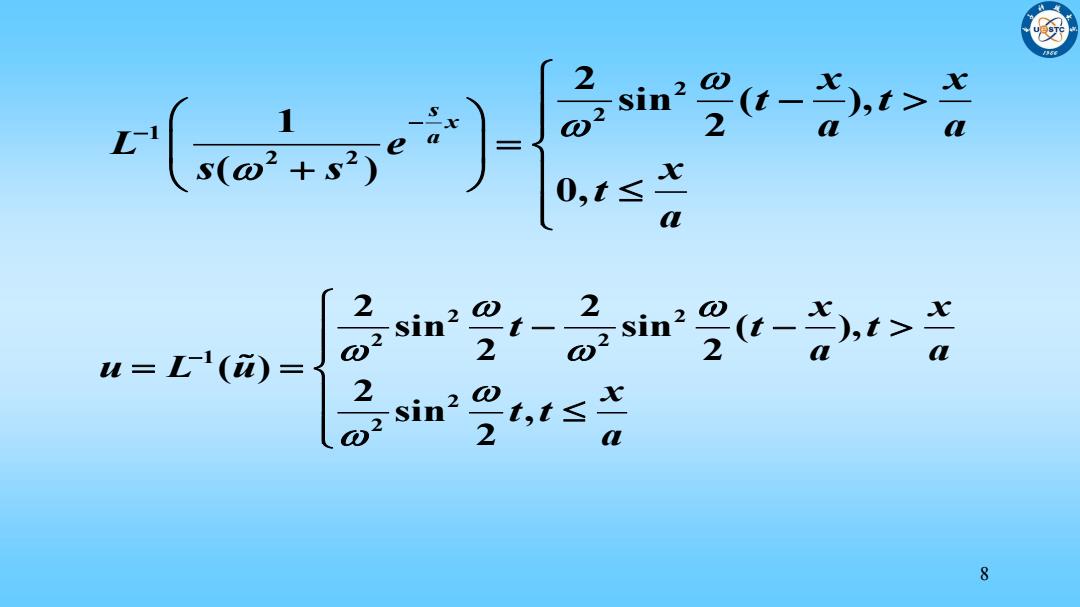
2 sin2 (t- ),t> 0,t≤ 2 2 sin2 sin2 (t- u='(m= 2 2 2 in t,t≤ 8
8 2 2 1 2 2 2 sin ( ), 1 2 ( ) 0, s x a x x t t a a L e s s x t a 2 2 2 2 1 2 2 2 2 sin sin ( ), 2 2 ( ) 2 sin , 2 x x t t t a a u L u x t t a