
常微分方程数值解 Euler法与修正的Euler法 误差分析 Range--Kutta公式
1 Euler法与修正的Euler法 误差分析 Range-Kutta公式 常微分方程数值解

Euler法与修正的Euler法 一阶常微分方程初值问题: =f(x,y),xxo dx 其中,y=yK)是未知函数, y(xo)=yo 右端函数x,y)是已知函数,初值y是已知数据。 数值方法一取定离散点:x<X1<2<…<Xy 求未知函数y(x)在离散点处的近似值 y1,Jy2,y3,…,yN y :f(x,y) dx ynti-yn=f(xn,yn) h 2
2 一阶常微分方程初值问题: 0 0 0 ( ) ( , ), y x y f x y x x dx dy 数值方法——取定离散点: x0 < x1 < x2 < ··· < xN 其中, y = y(x) 是未知函数, 右端函数 f(x, y )是已知函数, 初值 y0 是已知数据。 求未知函数 y(x) 在离散点处的近似值 y1 , y2 , y3 , ·····, yN ( , ) 1 n n n n f x y h y y f ( x , y ) dx dy Euler法与修正的Euler法

求解常微分方程初值问题的Euler方法 取定步长:h,记xn=xo+nh,(n=1,2,…,N) 称计算格式:y+1=ym+hxn,yn)为Euler公式。 对应的求初值问题数值解的方法称为Euler?方法。 例2用Euler法求初值问题 =y-y2,0<x<2 x 的数值解。 y(0)=1 解:记fc,y)=y一xy2,xm=nh (n=0,1,2,…,W) 由Euler公式得: yn+i =yn+h(yn-xnyn2) (n=0,1,…,N) 3
3 求解常微分方程初值问题的Euler方法 取定步长: h,记 xn = x0 + nh, ( n = 1,2, ···, N ) 称计算格式: yn+1 = yn + h f( xn , yn ) 为Euler公式。 对应的求初值问题数值解的方法称为Euler方法。 例2 用Euler法求初值问题 (0 ) 1 , 0 2 2 y y xy x dx dy 的数值解。 解: 记 f (x, y) = y- x y 2 , xn = nh (n = 0, 1, 2,···, N ) 由Euler公式得: yn+1 = yn + h( yn- xn yn 2 ) (n = 0, 1, ···,N)
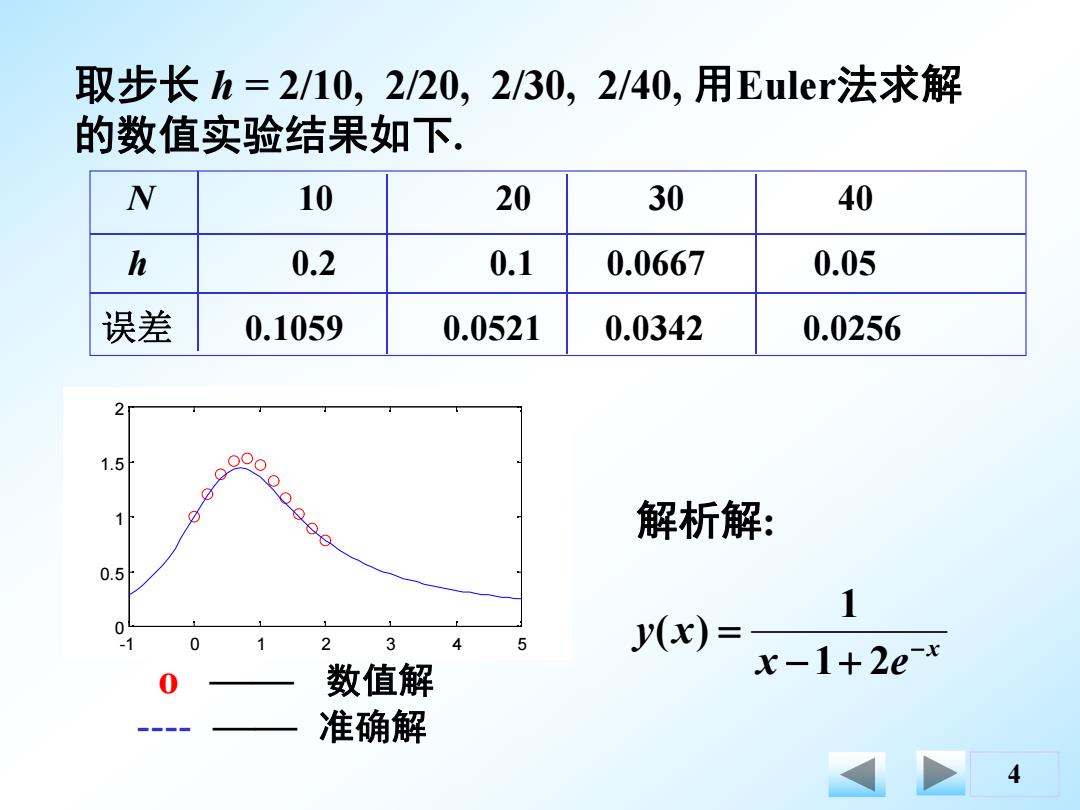
取步长h=2/10,2/20,2/30,2/40,用Euler法求解 的数值实验结果如下. N 10 20 30 40 h 0.2 0.1 0.0667 0.05 误差 0.1059 0.0521 0.0342 0.0256 2 1.5 o0 1 解析解: 0.5 1 0 0 2 3 5 y(x)= x-1+2e-x 0 数值解 准确解 4
4 取步长 h = 2/10, 2/20, 2/30, 2/40, 用Euler法求解 的数值实验结果如下. N 10 20 30 40 h 0.2 0.1 0.0667 0.05 误差 0.1059 0.0521 0.0342 0.0256 x x e y x 1 2 1 ( ) 解析解: -1 0 1 2 3 4 5 0 0.5 1 1.5 2 o —— 数值解 ---- —— 准确解

用数值积分方法离散化常微分方程 y'=f(化,y) →y'(x)=f(x,(x)c x)-(x)=∫fx,y(x)d 左矩形公式 fx,Jx)kef(x,y) yn+i-yn=hf (xn2yn) 梯形公式: ,x经)+fml 2 a1-J.=2f(x,.)+fc141l
5 y’ = f (x, y) 1 ( ) ( ) ( , ( )) 1 n n x x y xn y xn f x y x dx [ ( , ) ( , )] 2 ( , ( )) 1 1 1 n n n n x x f x y f x y h f x y x dx n n 梯形公式: ( , ) n 1 n n n y y hf x y 左矩形公式 ( , ( )) ( , ) 1 n n x x f x y x dx hf x y n n 用数值积分方法离散化常微分方程 1 1 ( ) ( , ( )) n n n n x x x x y x dx f x y x dx [ ( , ) ( , )] 2 n1 n n n n1 n1 f x y f x y h y y

由梯形公式推出的预一校方法: 儿-g=2Ucy+f小 → 「ya+1=yn+hf(xn,yn) y=.+fx,+f….川 预-校方法又称为修正的Euler法,算法如下 ki=f(xn,yn), k2=fxn+1,ynt h k1), yat=yn+lk+k2l 6
6 ( , ) ~ n n n n y y hf x y 1 )] ~ [ ( , ) ( , 2 n1 n n n n1 n1 f x y f x y h y y 1 1 1 [ ( , ) ( , )] 2 n n n n n n h y y f x y f x y 预-校方法又称为修正的Euler法,算法如下 k1 = f(xn , yn ) , k2 = f( xn+1 , yn+ h k1), [ ] 2 1 1 2 k k h y y n n 由梯形公式推出的预-校方法:

n 10 20 30 40 h 0.2 0.1 0.0667 0.05 误差2 0.0123 0.0026 0.0011 5.9612e-004 误差1 0.1059 0.0521 0.0342 0.0256 1.5 2 1.5 O000e 0.5 0.5 0 0 -1 0 3 -1 0 3 5 预-校方法,h=0.2时 欧拉方法, h=0.2时 误差最大值:0.0123 误差最大值:0.1059 7
7 -1 0 1 2 3 4 5 0 0.5 1 1.5 预-校方法, h=0.2时 误差最大值: 0.0123 -1 0 1 2 3 4 5 0 0.5 1 1.5 2 n 10 20 30 40 h 0.2 0.1 0.0667 0.05 误差2 0.0123 0.0026 0.0011 5.9612e-004 误差1 0.1059 0.0521 0.0342 0.0256 欧拉方法, h=0.2时 误差最大值: 0.1059

局部載断误差 设ym=y(cn),称Rn+1y(化+1)-y+1为局部截断误差. 由泰勒公式 y(x)=y(x)+(x-x)y(x)+au-x) y"(传) 2】 即 h' xa)=x)+f(xy)+2(5) Euler公式: yn+=ynt hf (xn yn) Euler公式的局部截断误差 y(xn+1)-yn+=y(xn)-yn+O(h2)=O(h2) 8
8 设 yn = y(xn ), 称 Rn+1=y(xn+1) - yn+1为局部截断误差. ( ) 2 ( ) ( ) ( ) ( ) ( ) 2 1 1 1 y x x y x y x x x y x n n n n n n n ( ) 2 ( ) ( ) ( , ) 2 1 y h y x y x hf x y n n n n 即 由泰勒公式 Euler公式: yn+1 = yn+ hf (xn , yn ) Euler公式的局部截断误差 y(xn+1) – yn+1=y(xn ) – yn+ O(h2) = O(h2)

收敛性分析 y(n+1)-yn+i=y(xn)-yn+O(h2) 定义:若一种数值方法对于任意固定的xm=xo+nh,当 h→0(同时n→oo)时,有ymy化),则称该方法是收敛 的.下面分析欧拉显式公式的收敛性: ynti=yn+hf(xn,yn) 1=y(x)+hf(x,y(x)) 单步计算的局部截断误差y(心m+1)一)+1为: h2 Wx)-万1=2y(5) 即存在常数C使en+1<Ch2. 9
9 :若一种数值方法对于任意固定的xn =x0+nh,当 h→0(同时n→∞)时,有yn→y(xn ),则称该方法是 的. 设 下面分析欧拉显式公式的 : 1 ( , ) n n n n y y hf x y 1 ( ) ( , ( )) n n n n y y x hf x y x 单步计算的 误差 y( xn1 ) yn1 为: 2 '' 1 1 ( ) ( ) 2 n n h y x y y 即存在常数C使 en+1< Ch2 . y(xn+1) – yn+1=y(xn ) – yn+ O(h2)

考虑无ymy化)条件下的整体截断误差: en+1=y(x+1)-y+l 由于 y(x)-yy(xi)+ 而 F-y=y(x)-yn+hf(xn>y(x,))-h(f(xy)) 若常微分方程的右端项f(xy)关于y满足李普希茨 条件,则有 y+1-卫n+i≤J(xn)-yn+hLy(xn)-yn) =(1+hL)(y(x,)-y) 10
10 而 由于 若常微分方程的右端项 f(x,y)关于y满足 条件, 考虑无 yn =y(xn )条件下的整体截断误差: 1 1 1 ( ) n n n e y x y 1 1 1 1 1 1 ( ) ( ) n n n n n n y x y y x y y y 1 1 ( ) ( , ( )) ( ( , )) n n n n n n n n y y y x y hf x y x h f x y 则有 1 1 ( ) ( ( ) ) n n n n n n y y y x y hL y x y (1 ) ( ( ) ) hL n n y x y