
极小、化方法 一、与线性方程组等价的变分问题 二、最速下降法 三、共轭梯度法(共轭斜量法) 四、预条件共轭梯度法
1 极小化方法 一、与线性方程组等价的变分问题 三、共轭梯度法(共轭斜量法) 四、预条件共轭梯度法 二、最速下降法

一、与线性方程组等价的变分问题 设x,y∈R”,记(x,y)=xTy (x,y)=(J乃,x); (t,y)=t(x,y); (x+yz)=(x,z)+(乃z); (,x)≥0,且(K,x)=0分x=0; 设A是n阶对称正定阵 (Ax,y)=(,Ay); (Ax,x)≥0,且(Ax,x)=0分x=0 2
2 设x, y∈Rn , 记 ( x , y) = x T y §( x, y ) = ( y, x ); §( tx, y ) = t ( x, y); §( x+ y, z ) = ( x, z ) + ( y, z ); §( x, x) ≥ 0, 且( x, x) = 0 x = 0; 设A是n阶对称正定阵 §( Ax, y ) = ( x, Ay ) ; §( Ax, x ) ≥0, 且( Ax, x) = 0 x = 0 一、与线性方程组等价的变分问题

设A对称正定,求解的线性方程组为 Ax=b (1) 其中A=(aj)∈Rx,x=(x1,x2,,xn),b=(b1,b2,,bn)月 对应的二次函数p:R"x”→R,称为模函数,定义为 --622宫A (2) 例:◆ A= -(x+6x+4x1x2)-(4x1+10x2) 3
3 1 2 1 2 1 ( ) , ( , , ..., ) , ( , , ..., ) n n T T ij n n A Ax b A a R x x x x b b b b 设 对称正定,求解的线性方程组为 ( ) 其中 1 1 1 ( , ) ( , ) 2 n n n n n ij i j i i i j i R R x Ax x b x a x x b x 对应的二次函数 : ,称为模函数,定义为 1 1 ( )= ( ) 2 2 2 2 1 2 1 2 1 2 4 , 1 0 ( 6 4 ) ( 4 1 0 例 ) 1 2 A = 2 6 1 ( ) = : 2 b x x x x x x x

模函数(二维) 正定 (a) (b) 负定 XTAX>0 XTAX<0 f(x) f(x) 2 2 工1 Z1 (c) (d) 正不定 不定 XTAX≥0 f(x) f(x) T2 W2 X1 4
4 模函数(二维) 正定 xT A x > 0 负定 xT A x < 0 正不定 xT A x ≥ 0 不定
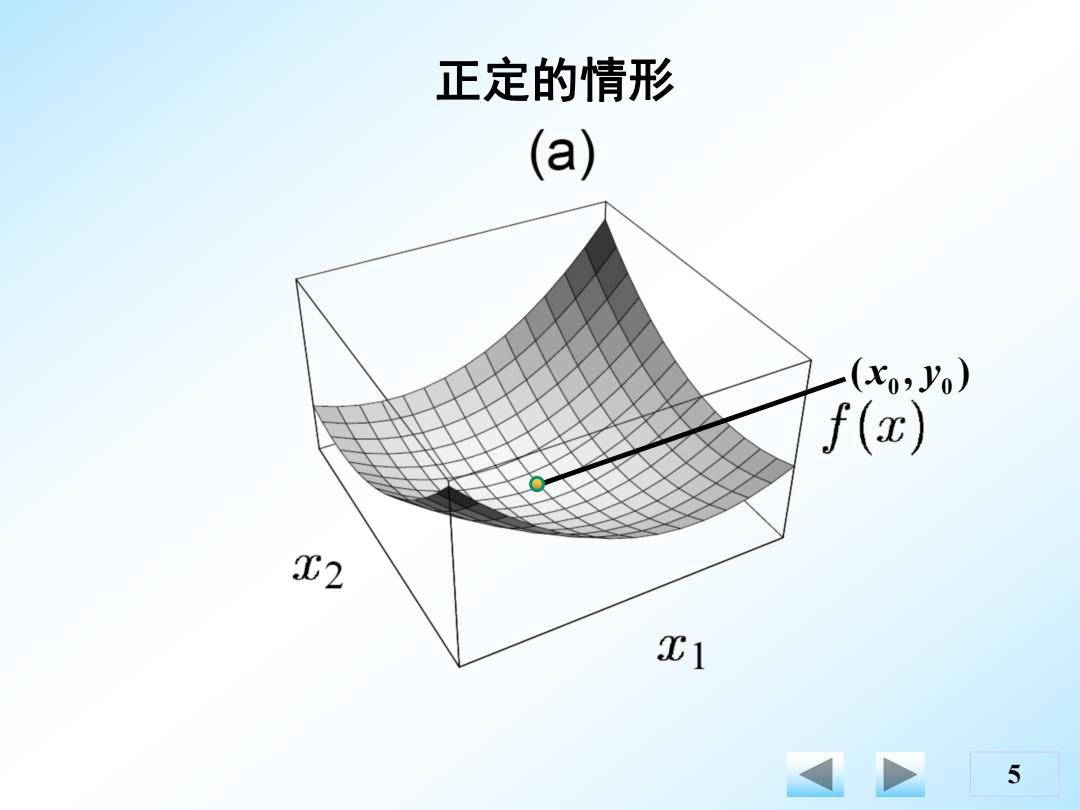
正定的情形 (a) (xo2Yo) f(x) T2 T1 5
5 ( , ) 0 0 x y 正定的情形

p(x)= 1 ag,x,-b,x, i=1 i=1 p有如下性质: (1)对一切x∈R",有7p(x)=grado(x)=Ax-b=-r(3) 证: 8眼-2,0=- i=1,2,,n wradel) =Ax-b=-r 6
6 1 3 n x R x x Ax b r 有如下性质: ( )对一切 ,有 ( )=grad ( )= - ( ) 1 1 , 1, 2, ..., ( ) n ij j i i j i T n a x b r i n x grad x Ax b r x x 证: 1 1 1 n n n ij i j i i i j i x a x x b x 1 ( ) 2

(2)对一切x,y∈R",a∈R (x+ay)=(A(x+ayhx+ay)-(hx+ay) (Ax,x)-(,x)+a(4,-a6,川+7(, +a-s+(4》 (4) pw)2,0-6. 7
7 2 2 , , 1 ( ) ( ( ), ) ( , ) 2 1 ( , ) ( , ) ( , ) ( , ) ( , ) 2 2 ( ) ( , ) ( , ) 4 2 n x y R R x y A x y x y b x y Ax x b x Ax y b y Ay y x Ax b y Ay y (2)对一切 ( ) x (Ax, x) (b, x) 1 ( )= 2

定理1 设A=(a)nxn为实对称正定矩阵,b,x∈R”,则x使二 次函数 f(x)=2(1,)-(6,) 取极小值分x是线性方程组Ax=b的解。 证明:必要性(解是极小值点).设山是A比,=b的解 →Au=b→ f四)=-2Aw,0) 对任意x∈R",只须证明fx)-f(W≥0 fx)-f=24,-6,e+A,) (A(x-W),(x-)≥0 2 8
8 设A =( aij )n×n为 , b , x∈Rn , 则 x使二 次函数 ( , ) ( , ) 2 1 f (x) Ax x b x 取极小值 x 是线性方程组Ax = b 的解。 证明: . 设 u 是 Ax = b的解 Au = b ( , ) 2 1 ( , ) ( , ) 2 1 f (x) f (u) Ax x b x Au u ( ( ),( )) 0 2 1 A x u x u 对任意 x∈Rn , 只须证明 f (x) – f (u) ≥ 0 ( , ) 2 1 f (u) Au u

充分性.设u使fx)取极小值.取非零向量x∈R", 对任意teR,有 fu+)=24+,u+)-,+) f(0+(Au-b,x)+)(, 令()=孔山+x),由于g()是关于t的连续函数,当 g'()=0,取得极小值。 另一方面令g()=几u+tx),当0时,g(0)=fu) 达到极小值。 于是g(0)=0,即 (Au-b,x)=0 → A 所以,u是方程组Ax=b的解. 9
9 .设u使 f(x)取极小值.取非零向量 x∈Rn , 对任意 t∈R , 有 ( ( ), ) ( , ) 2 1 f (u tx) A u tx u tx b u tx ( , ) 2 ( ) ( , ) 2 Ax x t f u t Au b x 令 g(t) = f( u + tx),由于g(t)是关于t的连续函数,当 g’(t) =0,取得极小值。 ( Au – b , x ) = 0 Au – b = 0 所以,u是方程组Ax=b的解. 另一方面令 g(t) = f( u + tx),当 t=0 时,g(0)= f(u) 达到极小值。 于是 g’(0) =0,即

求二次函数p(x)极小值点的一般方法是: 构造一个向量序列{x)},使p(x)→minp(x) 可以采取以下方法: (1)任取一个初始向量x), (2)构造迭代格式 x(k1)=x(k)+arp(), (k=0,1,…) 其中p是搜索方向,是搜索步长, (3)选择pk和a使得 (x)=o(xtap)<o(x() 则当k→o时,有p(x)→p(x)=mik(x) (4)算出误差限6,直到 x-x-Kε或r=b-ArKe 迭代为止。 10
10 ( ) ( ) ( ) ( ) min ( ) k k x x x x 求二次函数 极小值点的一般方法是: 构造一个向量序列 ,使 ( 0 ) ( 1) ( ) ( ) ( ) 1 2 , ( 0,1, ...) 可以采取以下方法: ( )任取一个初始向量 , ( )构造迭代格式 其中p 是搜索方向, 是搜索步长, k k k k k k x x x p k ( ) ( 1) ( ) ( ) ( ) ( ) * ( ) ( ) ( ) ( ) ( ) min ( ) n k k k k k k k k x R x x p x x x x (3)选择p 和 使得 则当k 时,有 ( ) ( 1) 4 (k) (k) ( )算出误差限 ,直到 < 或 r b-A < 迭代为止。 k k x x x