电子科技大学：《数值分析 Numerical Analysis》课程教学资源（课件讲稿）函数逼近

函数逼近 一般多项式函数逼近 切比雪夫多项式 勒让德多项式 正交多项式的应用 1

1 一般多项式函数逼近 切比雪夫多项式 勒让德多项式 正交多项式的应用 函数逼近

一般多项式函数逼近 问题：求二次多项式P)=a+x+2x2使 ∫IP(x)-sin(Pdk=min 连续函数的最佳平方逼近. 已知fx)∈C0,1,求多项式 0.5 P(x)=ao+ax+ax2+......+anx n 使得 L=[IP(x)-f(x)'dx=min 令 L(a,4,,)=0x'-fx -ad-a+( 2

2 问题: 求二次多项式 P(x)= a0 + a1x + a2x2 使 [ ( ) sin( )] min 1 0 2    P x x dx 0 0.5 1 0 1 连续函数的最佳平方逼近. 已知 f(x)∈C[0, 1], 求多项式 P(x) = a0 + a1x + a2 x2 + …… + an x n 使得 [ ( ) ( )] min 1 0 2     L P x f x dx     1 0 2 0 0 1 L(a ,a , ,a ) [ a x f (x)] dx n j j 令  n j           n j j j n j j L aj x dx a x f x dx f x dx 0 1 0 2 1 0 1 0 2 0 [ ] 2 ( ) [ ( )] 一般多项式函数逼近

L=ad-2afxf(xde+fLf(d -g-h 令 aL 0 i记：=xfx) 1 1/2… 1/(+1) 1/2 1/3… 1/(n+2) a 1/(n+1) …… 1/(2n+1) a. 系数矩阵被称为Hilbert矩阵 3

3          1 0 0 1 0 2 a x dx 2 x f (x)dx a L k n j j k j k                        n n b b b a a a n n n n           1 0 1 0 1/( 1) 1/(2 1) 1/ 2 1/ 3 1/( 2) 1 1/ 2 1/( 1) 系数矩阵被称为Hilbert矩阵  0   ak L 令   1 0 b x f (x)dx k 记 k           n j j j n j j L aj x dx a x f x dx f x dx 0 1 0 2 1 0 1 0 2 0 [ ] 2 ( ) [ ( )]

定义6.3设fx),gx)∈C[4,b],p(c)是区间[M,b]上的权函数，若等式 (f,g)=[p(x)f(x)g(x)dx=0 成立，则称fx),gx)在[4，b]上带权p(x)正交.当p(x)=1时，简称正交。 例1验证pc)=1,φ1心)=x在[-1,1上正交，并求二次多项式 p2(x)使之与p(x),p1)正交 解： ∫p(x)p,(x=∫1xk=0 4

4 定义6.3 设 f(x), g(x)∈C[a, b], ρ(x)是区间[a,b]上的权函数,若等式 ( , )  ( ) ( ) ( )  0  b a f g  x f x g x dx 成立,则称f(x), g(x)在[a, b]上带权ρ(x)正交. 当ρ(x)=1时,简称正交。 例1 验证 0(x)=1, 1(x)=x 在[ –1, 1]上正交, 并求二次多项式 2(x) 使之与0(x), 1(x)正交 ( ) ( ) 1 0 1 1 1 1 0 1      解:  x  x dx xdx

设p2x)=x2+421X+22 ∫1·g,(ec=0∫，xp,(x)k=0 ∫，(x2+ax+az)c=0∫x(x2+ax+a2)dc=0 2/3+222=0 422=-1/3 221/3=0 42=0 所以， 0,()=x2- 3 5

5 设 2(x) = x2 + a21x + a22 1 ( ) 0 1 1  2    x dx ( ) 0 1 1 2   x x dx 3 1 ( ) 2 所以  2 x  x  , ( ) 0 1 1 21 22 2     x a x a dx ( ) 0 1 1 21 22 2     x x a x a dx a22= - 1/3 a21=0 2/3+2a22 = 0 2a21 /3=0

切比雪夫多项式 Tx)=1,T1(x)=c0s0=x, T2(x)=c0s20 … Tn(x)=c0s(n0),… 1.递推公式： 由c0s(n+1)0+c0s(n-1)0=2cos0c0s(n0) 有cos(n+1)0=2cos0cos(n0)-c0s(n-1)0,从而 T+(x)=2x T(x)-Tn(x)(n=1) 所以，Tx)=1,T1)=x,T2x)=2x2-1,…, Tx)=cos(narccos(x)),........ 6

6 切比雪夫多项式 T0(x)=1, T1(x)= cos = x, T2(x)=cos2 ······ Tn (x)=cos(n),········· 有 cos(n+1)=2 cos cos(n) – cos(n-1) ，从而 Tn+1(x) = 2 x Tn (x) – Tn-1(x) (n ≥ 1) 所以, T0(x)=1, T1(x)=x, T2(x)=2x2 – 1 , ···, Tn (x)=cos(narccos(x)),········· 1.递推公式: 由 cos(n+1)+ cos(n-1) =2 cos cos(n)

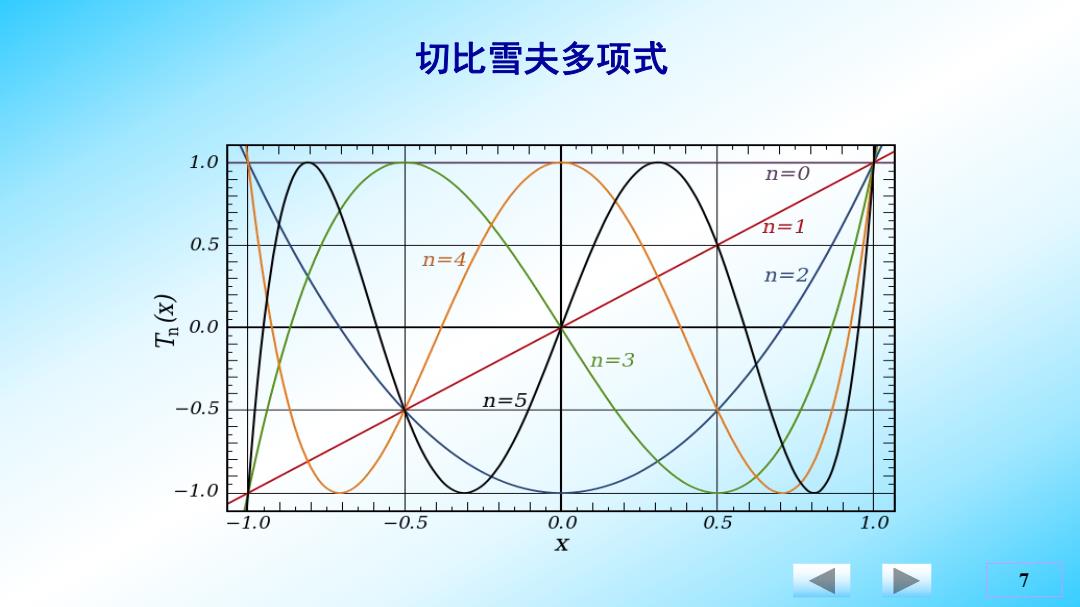
切比雪夫多项式 1.0 n=0 n=1 0.5 n=4 n=2 是 0.0 n=3 -0.5 n=5 -1.0 -1.0 -0.5 0.0 0.5 1.0 X 7

7 切比雪夫多项式

2.切比雪夫多项式的正交性 cos(me)cos(ne)de=0 (m≠n) -.w.国a =cosme cosn0de=0 所以，切比雪夫多项式在[-1,1]上带权 p(x)= V1-x2 正交 8

8 cos( )cos( ) 0 0    m n d (m ≠ n) cos cos 0 ( ) ( ) 1 1 ( , ) 0 1 1 2        m nd T x T x dx x Tm Tn m n 所以,切比雪夫多项式在[– 1 , 1]上带权 2 正交 1 1 ( ) x x    2.切比雪夫多项式的正交性

3切比雪夫多项式零点 T=cos0=x n阶Chebyshev多项式：Tm=cos(nd) T,(x)=cos(n arccosx) 取 narccosx (2k+1)π (k=0,1,…,n-1) 2 即 co() k=0,1,…,n-1) 9

9 3.切比雪夫多项式零点 n阶Chebyshev多项式: Tn =cos(n), 或 Tn ( x ) = cos(n arccos x ) 2 (2 1) arccos    k 取 n x (k=0,1,···,n-1 ) T1=cos=x ) 2 (2 1) cos( n k xk   即  (k=0,1,···,n-1 )

4.切比雪夫多项式的极性 Tn(c)的最高次项x的系数为2n-1. 若Pnx)=21-nTn(c),则在所有最高次项系数为1的n次多项式2nx) 中，有 max P (x)=min{maxe (x) -1≤x≤1 1≤x≤1 例如 t=-1+0.2k（k=0,1,2,…,10) = (k=0,1,2,…,10) ∂ P11c)=(x-x0)K-x1)…K-x10) Cu()(-to)(-)..(-to) 10

10 4.切比雪夫多项式的极性 Tn (x) 的最高次项 xn 的系数为 2n – 1 . 若Pn (x)= 21 – n Tn (x)，则在所有最高次项系数为1的n次多项式Qn (x) 中, 有 max | ( ) | min{ max | ( ) |} 1 1 1 1 P x Qn x x n   x     例如 tk = –1+0.2k ( k = 0, 1, 2, ···, 10) ) 22 (2 1) cos(    k xk ( k = 0, 1, 2, ···, 10)  P11(x)=(x – x0)(x – x1)······(x – x10) Q11(x)=(x – t0)(x – t1)······(x – t10)