
数值微分及微分方程数值解 >数值微分显式法 >隐式方法 >Lagrange插值函数方法 >外推算法
1 Ø数值微分显式法 Ø隐式方法 ØLagrange插值函数方法 Ø外推算法 数值微分及微分方程数值解

数值微分显式法 fa+创=a+a+空a+黄a+c的) 一阶向前差商 f(a)-(a-f):O(h) h fu-创=f@-r@+gfro)gfa+oy 一阶向后差商 fa=f@)-fa-+oh) h 4 2
2 数值微分显式法 ( ) ( ) 3! ( ) 2 ( ) ( ) ( ) (3) 4 2 3 f a O h h f a h f a h f a hf a ( ) ( ) ( ) ( ) O h h f a h f a f a 一阶向前差商 ( ) ( ) 3! ( ) 2 ( ) ( ) ( ) (3) 4 2 3 f a O h h f a h f a h f a hf a ( ) ( ) ( ) ( ) O h h f a f a h f a 一阶向后差商

fa+=o+ra+艺r@+分@+ 创=a-@+分ra-蛋@+ +-fa-0=2M@+营fPa+0a的 一阶中心差商 f(a)-f(a+h)-f(a-() 2h 二阶中心差商f"a=fa+)-2f@)+a-+0) h2 3
3 ( ) ( ) ( ) ( ) ( ) 2 2 2 O h h f a h f a f a h f a 二阶中心差商 ( ) 3! ( ) 2 ( ) ( ) ( ) (3) 2 3 f a h f a h f a h f a hf a ( ) ( ) ( ) ( ) 2 2 O h h f a h f a h f a 一阶中心差商 ( ) 3! ( ) 2 ( ) ( ) ( ) (3) 2 3 f a h f a h f a h f a hf a ( ) ( ) 3 ( ) ( ) 2 ( ) (3) 5 3 f a O h h f a h f a h hf a
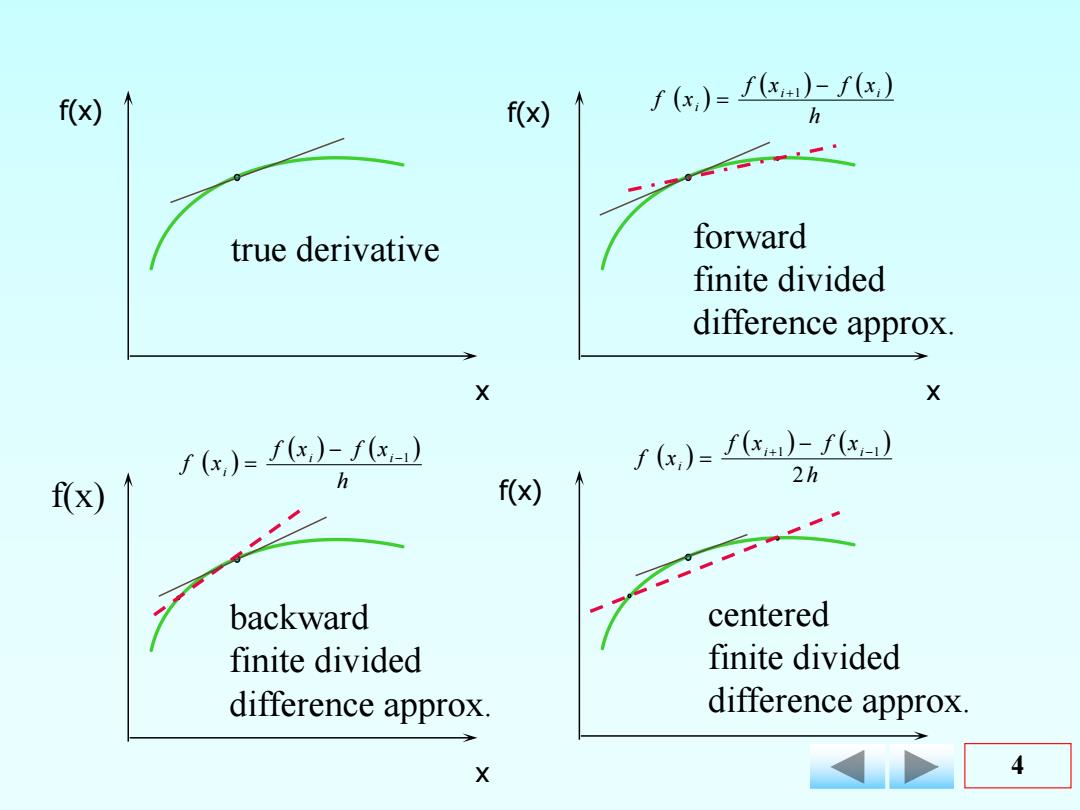
f(x) f(x) ()=()( h true derivative forward finite divided difference approx. X X f(G,)=f)-f f(x)=)-f 2h f(x) h f(x) backward centered finite divided finite divided difference approx. difference approx. X 4
f(x) x f(x) x f(x) x f(x) x true derivative forward finite divided difference approx. backward finite divided difference approx. centered finite divided difference approx. h f x f x f x i i i 1 h f x f x f x i i i 1 h f x f x f x i i i 2 1 1 4
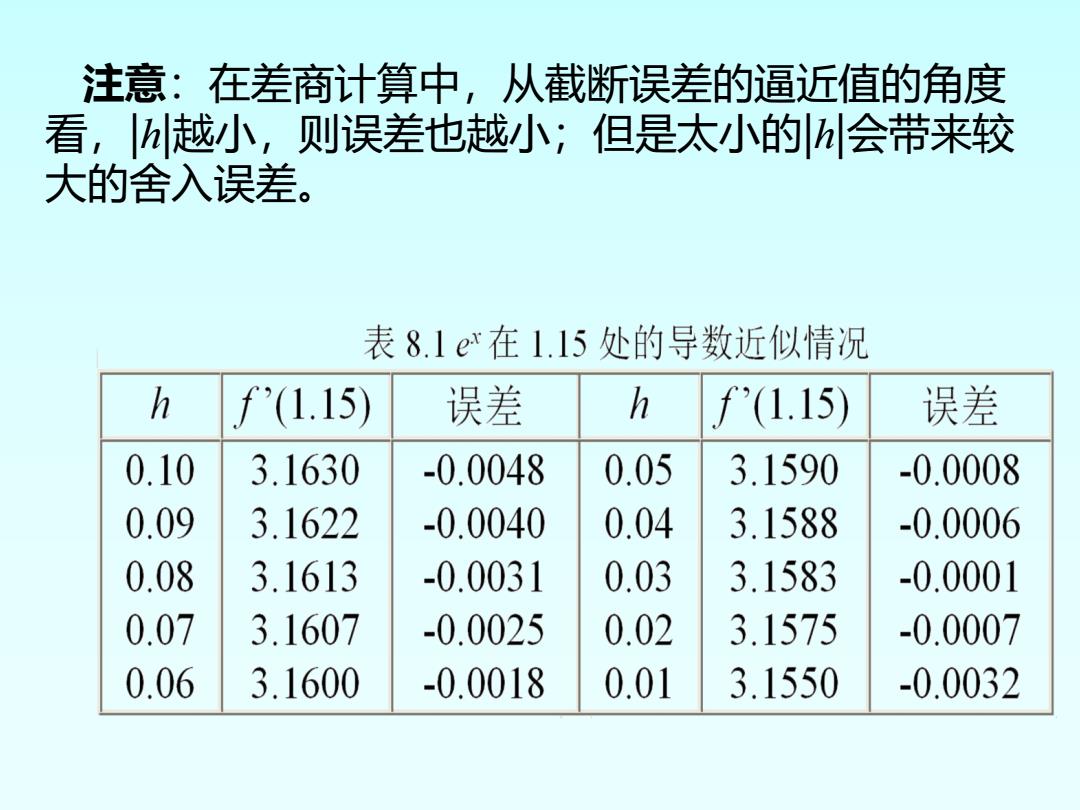
注意:在差商计算中,从截断误差的逼近值的角度 看,M越小,则误差也越小;但是太小的会带来较 大的舍入误差。 表8.1er在1.15处的导数近似情况 h f'(1.15) 误差 f'(1.15) 误差 0.10 3.1630 -0.0048 0.05 3.1590 -0.0008 0.09 3.1622 -0.0040 0.04 3.1588 -0.0006 0.08 3.1613 -0.0031 0.03 3.1583 -0.0001 0.07 3.1607 -0.0025 0.02 3.1575 -0.0007 0.06 3.1600 -0.0018 0.01 3.1550 -0.0032
注意:在差商计算中,从截断误差的逼近值的角度 看,|h|越小,则误差也越小;但是太小的|h|会带来较 大的舍入误差

隐式方法 设x=a+kh,(k=0,1,…,n)值 ow) 2h f(x)=')-2f')+f'+0) h2 令mk=f'(ck) (k=0,1,…,n) +4m=f()-f( k=1,2,…,n-1 q 6
6 ( ) ( ) 2 6 ( ) ( ) ( ) (3) 4 2 1 1 f x O h h h f x f x f x k k k k ( ) ( ) 2 ( ) ( ) ( ) 2 2 (3) 1 1 O h h f x f x f x f x k k k k 设 xk= a + k h ,( k =0,1,···,n) 值 令 mk = f ’(xk ) ( k=0,1,···,n) [ ( ) ( )] 1 1 1 1 3 4 k k k k k f x f x h m m m k=1,2,···,n-1 隐式方法

Lagrange:插值函数方法 f)-Etfx) f)-Etf k=0 k=0 xk=x0+kh (k=0,1,2) ()2x 2x-(x1+x2) 6(x)= 2h2 x)-存x-Xx-) 1 4(x)=- 2x-(x+x2) h2 (G) L2(x)= 2x-(x0+X1) 2h2 7
7 Lagrange插值函数方法 2 0 ( ) ( ) ( ) k k k f x l x f x 2 0 ( ) ( ) ( ) k j k j xk f x l x f xk = x0 + kh (k=0,1,2) ( ) ( )( ) ( ) ( )( ) ( ) ( )( ) 2 2 0 1 1 2 0 2 0 2 1 2 2 1 1 2 1 x x x x h l x x x x x h l x x x x x h l x 2 1 2 0 2 2 h x x x l x ( ) ( ) 2 0 1 2 2 2 h x x x l x ( ) ( ) 2 0 2 1 2 h x x x l x ( ) ( )

一阶导数近似 fx)=Et)fx) k=0 6(x)= 2x-(x1+X2) f,)26-3x)+4f)-f,】 22 1 ()=- 2x-(x+x2) f'(x1)≈[-f(x)+f(x2〗 h2 2h 2x-(x+1) f')*2h/,)-4fx)+3fx,J 5(x)= 2h2 二阶导数近似 6(x)=F 2 (x)=- 1 12(x)= h2 "(x)≈fxn)-2f)+fx2) h 8
8 0 2 1 h l(x) 1 2 2 h l(x) 2 2 1 h l(x) ( ) [ ( ) ( ) ( )] ( ) [ ( ) ( )] ( ) [ ( ) ( ) ( )] 2 0 1 2 1 0 2 0 0 1 2 4 3 2 1 2 1 3 4 2 1 f x f x f x h f x f x f x h f x f x f x f x h f x 2 0 2 1 2 h f x f x f x f x ( ) ( ) ( ) ( ) 2 1 2 0 2 2 h x x x l x ( ) ( ) 2 0 1 2 2 2 h x x x l x ( ) ( ) 2 0 2 1 2 h x x x l x ( ) ( ) 2 0 ( ) ( ) ( ) k j k j xk f x l x f 一阶导数近似 二阶导数近似

外推算法 G0=2+)-fx-] G(h)=f(x)(a)-Kat)fa) 2h G(h/2)=f'(x)+ah2/4+&2h4/16+… 4Gh/2)-G四=f'(x)-3a,h/4+… 3 4G.3-6.h G,(h) 4m-1 f(x)-G(h)=O(h2(m1) 9
9 外推算法 ( ) [ f (x h) f (x h)] h G h 2 1 G(h) f (x) 1h 2 2h 4 4 1 2 4 1 1 m m m m m G h h G G h ( ) ( ) ( ) ( ) ( ) ( ) 2( 1) m f x Gm h O h G(h/ 2) f (x) 1h 2 / 4 2h 4 / 16 3 4G(h/ 2) G(h) f (x) 3 2h 4 / 4 ( ) ( ) ( ) ( ) 2 2 O h h f a h f a h f a
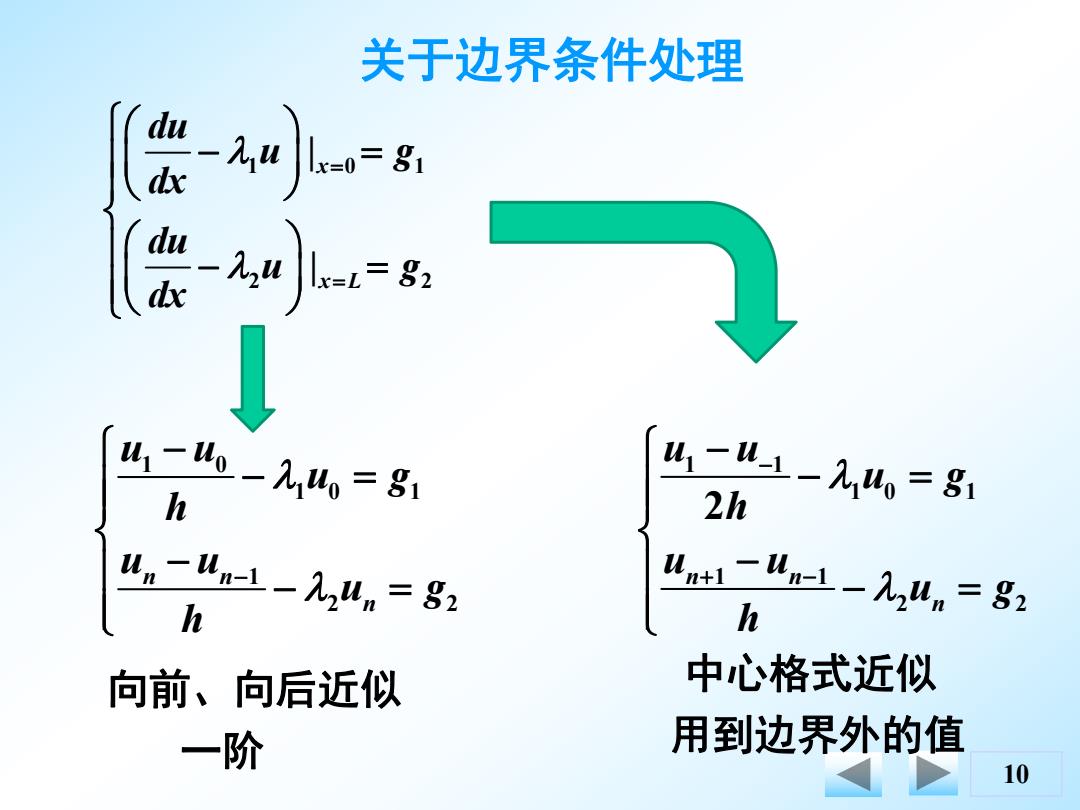
关于边界条件处理 du d lk=0=81 du d 41一46-2,4=81 h 41-WL-2,W=81 2h un -Un=1-hun 82 h Unti -un-1-hun 82 h 向前、向后近似 中心格式近似 一阶 用到边界外的值 10
10 关于边界条件处理 1 0 1 2 2 | | x x L du u g dx du u g dx 1 0 1 0 1 1 2 2 n n n u u u g h u u u g h 1 1 1 0 1 1 1 2 2 2 n n n u u u g h u u u g h 向前、向后近似 一阶 中心格式近似 用到边界外的值