电子科技大学：《数学物理方程与特殊函数 Mathematical Physics Equations with Special Function》课程教学资源（课件讲稿）第五章 积分变换 5.1 Fourier变换（1/2）

激学物理方程与特殊函激精品课程 第五章积分变换 主讲：李明奇副教授

第五章 积分变换 主讲：李明奇 副教授

§5.1 Fourier?变换 x)定义在(-0，+o)内，且在任一有限区间[L,L]上分段光滑，则可 以展开为Fourier级数 )=2+2(aeos"+sin"T） d.cos ,(n=0,1,2,) ()sin s ds 1768-1830

2 f(x) 定义在 (-∞ ,+∞ ) 内，且在任一有限区间 [-L,L]上分段光滑，则可 以展开为Fourier级数 0 0 ( ) cos sin 2 n n n a n x n x f x a b L L               1 ( )cos ,( 0,1,2, ) 1 ( )sin L n L L n L n s a f s ds L L n n s b f s ds L L               §5.1 Fourier变换 1768 –1830

Fourier变换 f(o)=∫f(x)eio* Fourier.逆变换 fe)=2元Jf@e4w 记号」 子(o)=F(f(x) F-F(f(x))=f(x) Fourier and Laplace Transforms f(x)=F-(j())=F-(F(f(x)) RJ Seerends,H.G ter Morsche. Cvan den Berg andE.Mvan de vrie 款数加a新 Conoltson,Fourier Serics and Iegnl (x)*(x)=(x-s)f(s)ds 希I出

3 Fourier变换 ˆ j ( ) ( ) x f f x e dx        1 ˆ j ( ) ( ) 2 x f x f e d         Fourier逆变换     1 1 ˆ f x F f F F f x ( ) ( ) ( ( ))        ˆ 记号 f F f x ( ) ( )     1 F F f x f x ( ) ( )   f x f x f x s f s ds 1 2 1 2 ( ) ( )          

一、一维Fourier变换的基本性质 性质1（线性定理 )F(af(x)+B5(x))=aF((x))+BF((x)) 性质2（卷积定理） F(f(x)*(x))=F((x))F((x)) 性质 3(乘积定理)F((,()=2元FUe》*FU.》 性质4（原象的导数定理） F(f(x))=j@F(f(x)) CHAMAN A HALLOIC APLID MATHEMATIS w的eH中性填光线批店 F((x))=(j@)F(f(x)) FOURIER SERIES IN SEVERAL VARIABLES WITH APPLICATIONS TO PARTIAL 性质5（象的导数定理） DIFFERENTIAL dF())-F(-()) EQUATIONS Vietor L.Shapiro

4 一、一维Fourier变换的基本性质 性质1 （线性定理） F f x f x F f x F f x     1 2 1 2 ( ) ( ) ( ) ( )         性质2 （卷积定理） F f x f x F f x F f x  1 2 1 2 ( ) ( ) ( ) ( )       性质3 （乘积定理）  1 2 1 2  1 ( ) ( ) ( ( )) ( ( )) 2 F f x f x F f x F f x        ( )( ) (j ) ( ) k k F f x F f x   性质4 （原象的导数定理） F f x F f x  ( ) j ( )      性质5 （象的导数定理）  ( ) j ( )    d F f x F xf x d  

性质6（延迟定理） F(f(x-x))=e-iaF(f(x)) 性质7（位移定理） F(ej*f(x))-j(@-@) 性质8（积分定理） r(d)-() 性质9（广义函数） F((x))=()e-I@dx =e-iooxo=1 F(6(x-5)=∫6(x-5)e-jk=ej 性质10（相似定理） r()- 5

5 性质6 （延迟定理）     0 j 0 ( ) ( ) x F f x x e F f x     性质7 （位移定理）   0 j 0 ˆ ( ) ( ) x F e f x f      性质8 （积分定理）     1 ( ) ( ) j x F f d F f x         j j 0 ( ) ( ) 1 x x F x x e dx e x             性质9 (广义函数  )      j j x F x x e dx e                性质10 (相似定理 )   1 ˆ F f ax f ( ) ( ) a a 

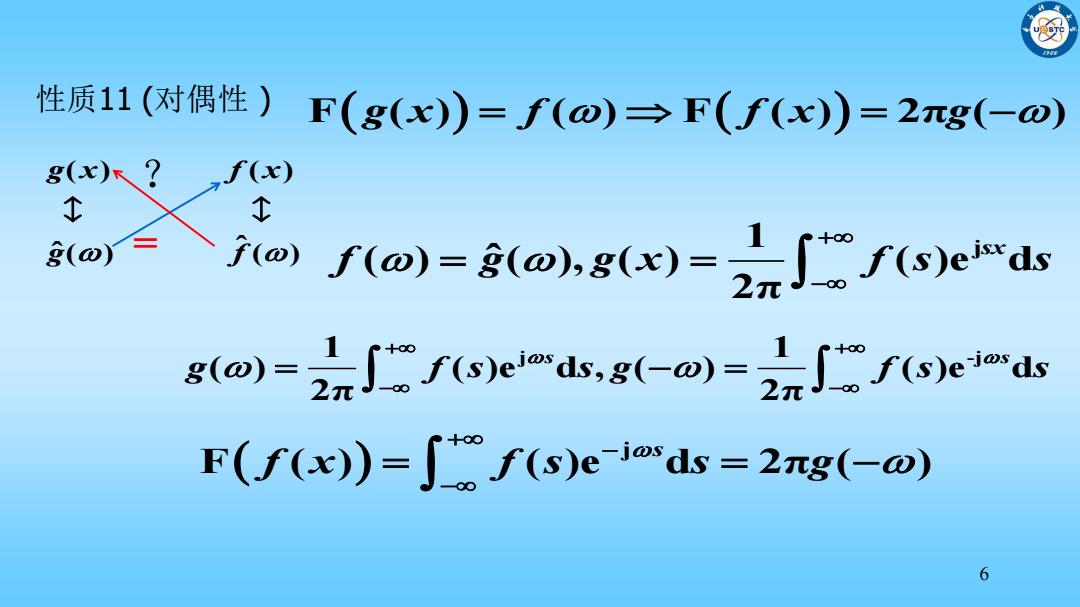
性质11（对偶性）F(g(x)=f(o)→F(.f(x)=2g(-D) 8(x)R? ,f(x) ① () )o)=(o.g(x)=2元J」f(s)eds g@)=2元()ds,g-m)=2元()eds F(f(x))=Sf(s)e-j@ds=2ng(-@) 6

6 性质11 (对偶性 ) F ( ) ( ) F ( ) 2  g x f f x g          π ( ) 1 j ( ) ( ), ( ) ( )e d ˆ 2π sx f g g x f s s        ( ) ( ) ˆ ˆ( ) ( ) g x f x g f   ？ = 1 1 j -j ( ) ( )e d , ( ) ( )e d 2π 2π s s g f s s g f s s                j F ( ) ( )e d 2π ( ) s f x f s s g         

性质12(Parseval公式) ∫f(vax=2元∫Fwd@ Parseval定理指出，一个信号所含有的能量（功率）恒等于此信 号在完备正交函数集中各分量能量（功率）之和。它表明信号在时 域的总能量等于信号在频域的总能量，即信号经傅里叶变换后其总 能量保持不变，符合能量守恒定律。 7

7 Parseval 定理指出，一个信号所含有的能量（功率）恒等于此信 号在完备正交函数集中各分量能量（功率）之和。它表明信号在时 域的总能量等于信号在频域的总能量，即信号经傅里叶变换后其总 能量保持不变，符合能量守恒定律。 性质12 (Parseval 公式 ) + 2 2 1 ˆ ( )d ( ) d 2π f x x f         

二、正余弦变换 定义2 Fourier余弦变换 f(o)=∫f(x)cos@xdx 定义3 Fourieri逆余弦变换 fe)-2元(-xwxdo 定义4 Fourier正弦变换 f.(o)=∫f(x)sin@xdx DISCRETE COSINE AND SINE TRANSFORMS 定义5 Fourier逆正弦变换 fx)=20元.(o)Dsinwxdo 在静止图像编码标准PEG中，在运动图像编码标准MPEG和 MPEG的各个标准中都使用了离散余弦变换

8 定义2 Fourier余弦变换 0 ˆ f f x x x c ( ) ( )cos d      定义3 Fourier逆余弦变换 0 2 ˆ ( ) cos d π c f x f x       ( ) 定义4 Fourier正弦变换 0 ˆ f f x x x s ( ) ( )sin d      定义5 Fourier逆正弦变换 0 2 ˆ ( ) ( )sin d π s f x f x       二、正余弦变换 在静止图像编码标准JPEG中，在运动图像编码标准MJPEG和 MPEG的各个标准中都使用了离散余弦变换