
§7.2 Besseli函数的母函数 一、】 esselE函数{Jn(x)} 的母函数 e-2() e产-2)- )] ■1730年左右,de Moivre用母函数来求解 Fabonaceis数列通项公式 1748年:Euler发展了母函数, 并用于解决分配问题 de Moivre 19世纪初,Laplace深入 研究 了母函数,并用于 处型概率同 PROBLEMS IN Euler ANALYSIS
§7.2 Bessel函数的母函数 2 一、Bessel函数 的母函数 2 0 1 ! 2 x k z k k x e z k 1 2 0 1 ( ) ! 2 x l z l l x e z l 1 ( ) 2 0 0 1 1 ( ) ! 2 ! 2 x k l z z k l k l x x e z z k l J x n ( )
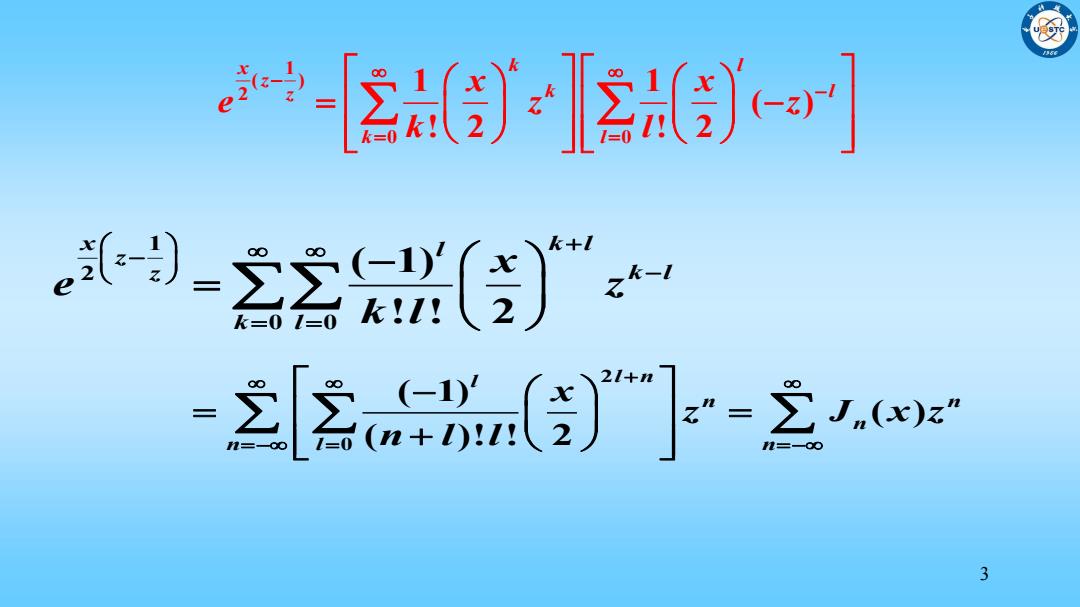
-2-引 9-22( k+ 2k-1 k三0 三房(g-空ws 3
3 1 ( ) 2 0 0 1 1 ( ) ! 2 ! 2 x k l z z k l k l x x e z z k l 1 2 0 0 ( 1) ! ! 2 x k l l z z k l k l x e z k l 2 0 ( 1) ( ) ( )! ! 2 l l n n n n n l n x z J x z n l l

BesselE函数的母函数 w(e)=e(-) 令z=jeie ekomo-cos(xcos)+jsin(xcose)=)i"em -J(x)+>[J(x)j"eim+J()j-"e-wo] =J(x)+2>j"J(x)cosne 4
4 Bessel函数的母函数 令 j z ej j cos j cos( cos ) jsin( cos ) ( )j x n n n n e x x J x e 1 2 ( ) x z z w z e 0 1 ( ) 2 j ( )cos n n n J x J x n j j 0 1 ( ) ( )j ( )j n n n n n n n J x J x e J x e
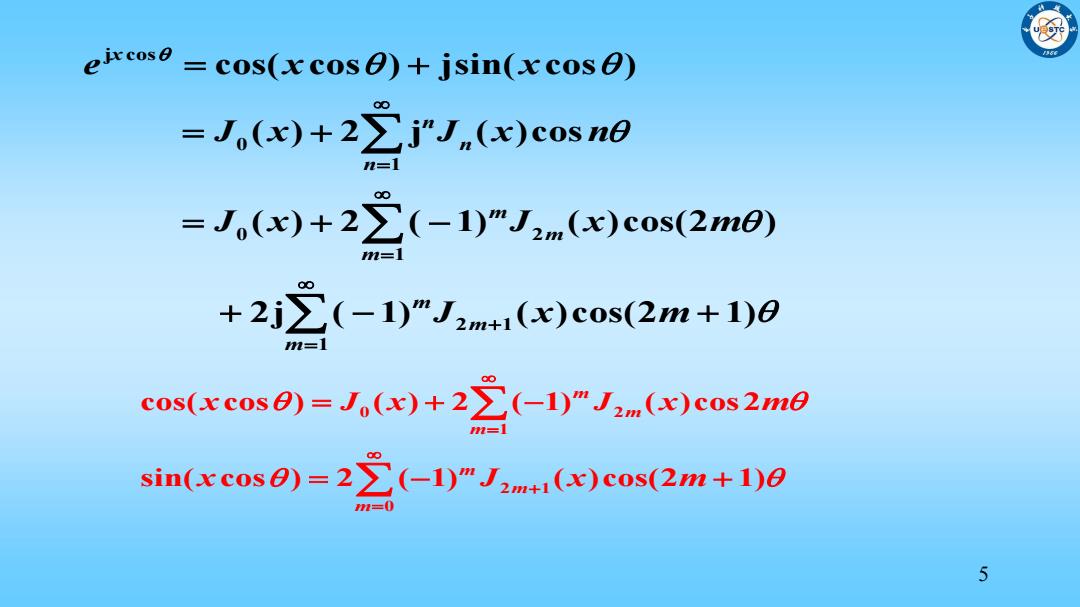
eixcoso cos(xcose)+jsin(xcose) =J(x)+2>j"J(x)cosne = =J(x)+2∑(-1)"J2m(x)cos(2m0) =1 +2j∑(-1)"J2m+1(x)c0s(2m+1)8 cos(xcos0)=J(x)+2>(-1)"J2m(x)cos2m0 I- sin(xcose)=2>(-1)"J2m(x)cos(2m+1)0 =0 5
5 j cos 0 1 0 2 1 2 1 1 cos( cos ) jsin( cos ) ( ) 2 j ( )cos ( ) 2 ( 1) ( )cos(2 ) 2j ( 1) ( )cos(2 1) x n n n m m m m m m e x x J x J x n J x J x m J x m 0 2 1 2 1 0 cos( cos ) ( ) 2 ( 1) ( )cos2 sin( cos ) 2 ( 1) ( )cos(2 1) m m m m m m x J x J x m x J x m

二、Bessel函数的积分表达式 Laurent展式的系数公式 1=-o Laurent展式的系数公式 w=2j∮eae 取C为单位圆 6
6 二、Bessel函数的积分表达式 Laurent展式的系数公式 1 2 1 1 1 ( ) d 2 j x z z n C n J x e z z 取C为单位圆 Laurent展式的系数公式 1 0 1 ( ) d 2πj ( ) n n C f z C z z z 1 ( ) 2 ( ) x z z n n n n n n e C z J x z
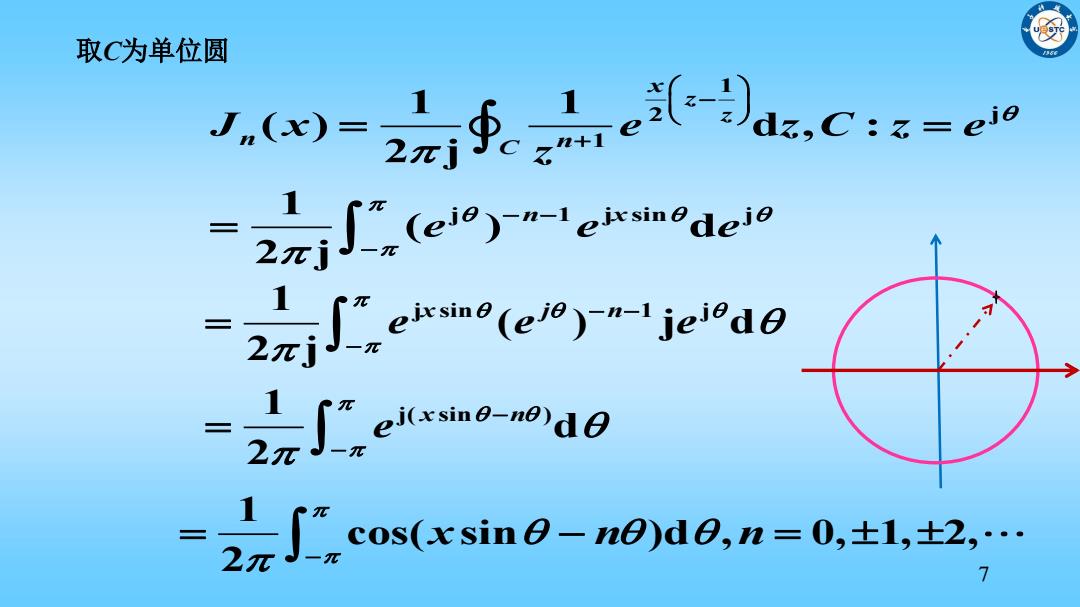
取C为单位圆 .a=2∮.e-.cz zzj∫(e)w'enae0 2zj∫eaey-tiea0 2c∫d =2元Jos(esin0-n08,n=0,士l,2,… 7
7 j sin 1 j j( sin ) 1 ( ) j d 2 j 1 d 2 x j n x n e e e e 1 cos( sin )d , 0, 1, 2, 2 x n n 取C为单位圆 1 2 j 1 j 1 j sin j 1 1 ( ) d , : 2 j 1 ( ) d 2 j x z z n C n n x J x e z C z e z e e e

Bessel函数的递推公式 J(x)=1- 23++(-02次+ 北6 七2e 2+2*(2 2 xs 1(x)=-23.2:+2230 x7 27.34:+…+(-1))2+ 七2+1 十 22k+k(k+1)9 {}=r益a时 x2k+利 22*2I(k+10T=-(-) 22k+1k:(k+1)H J()=-J) dx 8
8 Bessel函数的递推公式 2 4 6 2 0 2 4 2 6 2 2 2 ( ) 1 ( 1) 2 2 (2!) 2 (3!) 2 ( !) k k k x x x x J x k 3 5 7 2 1 1 3 5 7 2 1 ( ) 2 2 2! 2 2!3! 2 3 ( 1) ! 4! 2 !( 1)! k k k x k x x k x x J x 1 2 2 2 1 2 2 2 2 2 2 2 2 1 1 d ( 1) (2 2) ( 1) d 2 [ ( 1) ( 1)!] 2 [( 1)!] 2 !( 1)! k k k k k k k x k k x k k x x k k k 0 1 d ( ) ( ) d J x J x x

o-[22++(- 七2+2 22k+1k!(k+1)月 七2k+1 2+…+2y+ x2k d =xJ(x) xJ(x)川=xJ(x) dx dl.(-i(-1) 七2n+2m n1=0 2"+2mm!T(n+m+1) =x"∑(-1) 七n+21-1 1=0 "2*2mmr(n+m) d =x"J(x) I"J(="Js(c)
9 2 4 2 2 1 3 2 1 d [ ( )] ( 1) d 2 2 2! 2 !( 1)! k k k d x x x xJ x x dx k k 1 0 d [ ( )] ( ) d xJ x xJ x x 2 2 2 0 2 1 2 1 0 d d [ ( )] ( 1) d d 2 ! ( 1) ( 1) 2 ! ( ) n m n m n n m m n m n m n m m x x J x x x m n m x x m n m 1 ( ) n x J x n 3 2 1 2 2 2 2 2 2 2 2 0 ( 1) 2 2 ( !) 1 ( 1) 2 2 ( !) ( ) k k k k k k x x x k x x x k xJ x 1 d [ ( )] ( ) d n n x J x x J x n n x

&eJ,ax1=Jw→J4(+Ww=.,) &xJ.(x1=-xJ()→xJ(x)-Jn(心))=-x+1(x)) Besseli函数的递推公式 Jn-1()+Jn1(x)=2n(x) Jm-1(x)-Jm+1(x)=2J(x) 10
10 1 d [ ( )] ( ) d n n x J x x J x n n x 1 d [ ( )] ( ) d n n x J x x J x n n x 1 ( ) ( ) ( ) xJ x nJ x xJ x n n n 1 ( ) ( ) ( ) xJ x nJ x xJ x n n n 1 1 1 1 2 ( ) ( ) ( ) ( ) ( ) 2 ( ) n n n n n n J x J x nJ x x J x J x J x Bessel函数的递推公式
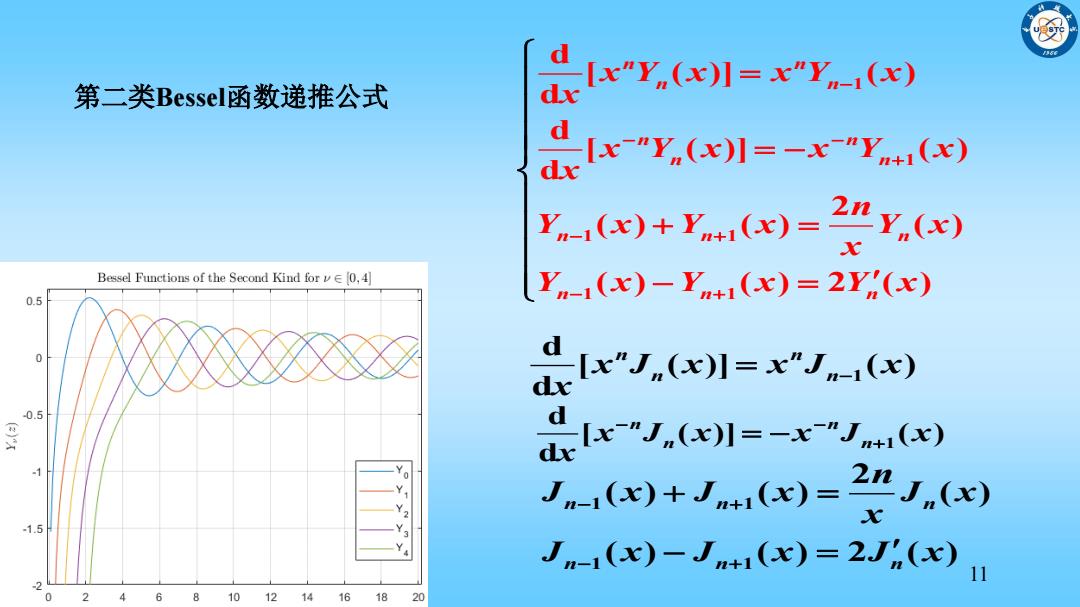
[x"Y (x)1=x"Y(x) 第二类BesselF函数递推公式 dx dIx (x)1=-x-"Y() dx y.()+yn,x)=21y.(e) Bessel Functions of the Second Kind for 0,4] 0.5 Ym-(x)-Y+(x)=2Y(x) [x”Jn(x)】=x”Jm-1(x) dx -0.5 d [x"J(x)]=-x"J(x) dx 1))+J+1(e)=2J.(e) -1.5 J(x)-J(x)=2J(x) 0 2 6810121416 18 20
11 第二类Bessel函数递推公式 1 1 1 1 1 1 d [ ( )] ( ) d d [ ( )] ( ) d 2 ( ) ( ) ( ) ( ) ( ) 2 ( ) n n n n n n n n n n n n n n x Y x x Y x x x Y x x Y x x n Y x Y x Y x x Y x Y x Y x 1 d [ ( )] ( ) d n n x J x x J x n n x 1 d [ ( )] ( ) d n n x J x x J x n n x 1 1 1 1 2 ( ) ( ) ( ) ( ) ( ) 2 ( ) n n n n n n n J x J x J x x J x J x J x