电子科技大学：《数学物理方程与特殊函数 Mathematical Physics Equations with Special Function》课程教学资源（课件讲稿）第五章 积分变换 5.3 Laplace变换

§5.3 Laplace变换 一、Laplace2变换的定义 L(f)=子(s)=∫f()e”t 0='(）-27we-2 e6 黎曼-梅林反演公式 PIERRE- SIMON LAPLACE Finsleri调和映射与 Laplace算子 1749-1827 餐司伊能越超作剂 2ifi F(s)e"ds,t 0,Res=>o f0)= ∫o+jao A Life in Exact Science 0,t<0 CHARLES COULSTON 349

§5.3 Laplace变换 一、Laplace变换的定义   0 ( ) ( ) ( ) st L f t f s f t e dt      黎曼-梅林反演公式 j 0 j 1 ( ) , 0,Re ( ) 2 j 0, 0 st F s e ds t s f t t                     2   j j 1 j j 1 1 ( ) ( ) ( ) lim ( ) 2 j 2 j N st st N N f t L f s f s e ds f s e ds                    

例求函数f(t)=ce“ 的Laplace2变换 解： L(ce“)-J0ce"e"t=_ ce-(s-mt s-a =。m ce-(s-a) t→+o0 aga[ee-0] sa Res>Rea

( ) at f t ce    ( ) 0 0 s a t at at st ce L ce ce e dt s a           例 求函数 的Laplace变换 ( ) lim s a t t c ce s a s a        ,Re Re c s a s a    Re( ( )) j Im( ( )  ) lim t s a t a s t c c e s a s a e              解：

二、Laplace3变换的性质 1.线性定理 L(af(t)+azf(t))=aL((t))+aL((t)) L(aF(s)+azF(s))=aL(F(s))+a2(F2(s)) 2.卷积定理1 ((t)*())=L(())L(()) 3.延迟定理 L(f(t-))=e-"L(f(t)) 4.位移定理L(e"f(t)=F(s-,Re(s-m)>oo 5.相似定理若c>0,则 (fc)=r(8 4

            1 1 2 2 1 1 2 2 1 1 1 1 1 2 2 1 1 2 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) L a f t a f t a L f t a L f t L a F s a F s a L F s a L F s          1.线性定理 3. 延迟定理  ( ) ( )    s L f t e L f t      4. 位移定理   0 ( ) ( ),Re( ) at L e f t F s a s a      5 . 相似定理 若 c > 0 ， 则   1 ( ) s L f ct F c c        2. 卷积定理 L f t f t L f t L f t  1 2 1 2 ( ) ( ) ( ) ( )         二、 Laplace变换的性质 4

6.微分定理 L(f(t))=sL(f(t))-f(0) L(f"(t)=s2L(f(t)-sf(0)-f'(0) L(f(）=sL(f0)-s-f0-s-2f'(0--子-(0) 7.积分定理 8.象函数的微分定理 Fs)=L(-rf) 9.象函数的积分定理 rer=(fe） 5

6 . 微分定理         2 ( ) ( ) (0) ( ) ( ) (0) (0) L f t sL f t f L f t s L f t sf f         7. 积分定理     0 1 ( ) ( ) t L f d L f t s     8. 象函数的微分定理 ( ) ( ) ( )   n n n d F s L t f t ds   9. 象函数的积分定理 ( ) ( ) s f t F d L t            5     ( ) 1 2 ( 1) ( ) ( ) (0) (0) (0) n n n n n L f t s L f t s f s f f         

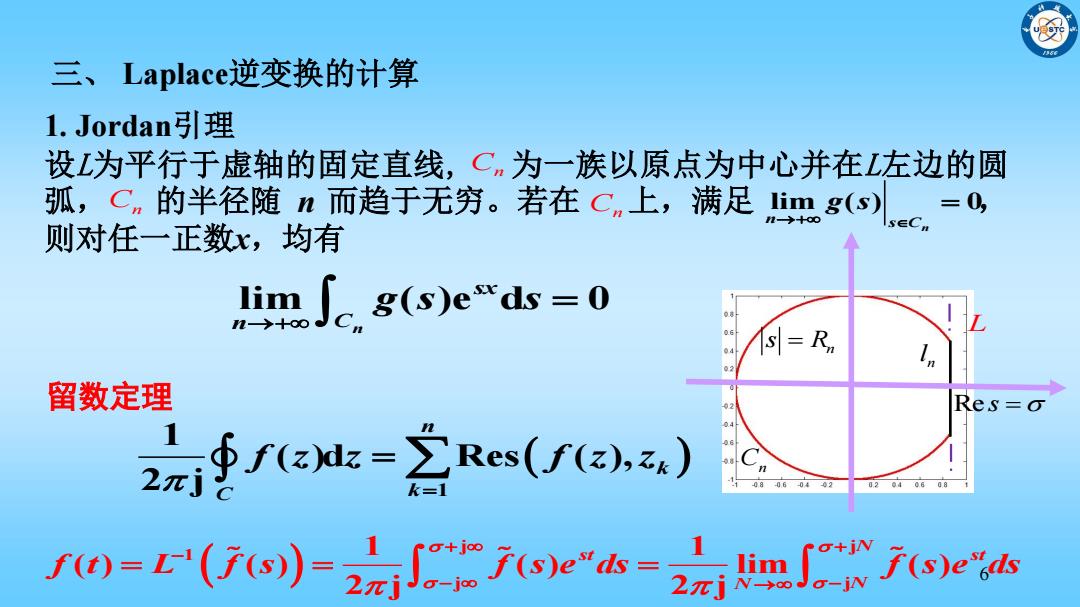
三、Laplace逆变换的计算 1.Jordan引理 设L为平行于虚轴的固定直线，C,为一族以原点为中心并在L左边的圆 弧，Cn的半径随n而趋于无穷。若在C,上，满足img(s) =0) 则对任一正数x,均有 limf g(s)e"ds=0 =R 留数定理 Res=o 2∮fau=2es(fea.) 0806040 02040608 fW='(f)=2元Jgf)ek= o+jN 2元j mw(s)e'ds lim

6 1. Jordan引理 设L为平行于虚轴的固定直线, 为一族以原点为中心并在L左边的圆 弧， 的半径随 n 而趋于无穷。若在 上，满足 ， 则对任一正数x，均有 Cn lim ( ) 0 n n s C g s    lim ( )e d 0 n sx n C g s s    Cn Cn Cn Re s  n s R  n l L   j j 1 j j 1 1 ( ) ( ) ( ) lim ( ) 2 j 2 j N st st N N f t L f s f s e ds f s e ds                       1 1 ( )d Res ( ), 2 j n k C k f z z f z z      留数定理 三、 Laplace逆变换的计算

imc.(s)eds0 =')2ae6 lim o+jN F(s)e"ds 。，。 2元j N-→owo-jN 2∮/址-会cs(a.） 2.展开定理 f=∑Res(f(s)e,s) Res=o 08060402 02040608 7

7 2. 展开定理 ( ) Res ( ) ,   st k k f t f s e s   Cn Re s   n s R  nl L lim ( )e d 0 n sx n C g s s      1 1 ( )d Res ( ), 2 j n k C k f z z f z z        j j 1 j j 1 1 ( ) ( ) ( ) lim ( ) 2 j 2 j N st st N N f t L f s f s e ds f s e ds                    

例己知 F(s) S (+a)(s+B)2 求L(F(s) 解： ron=ratatj z+成+】 -g+a小+m++时em (B-a) 8

8 例 已知 求    2 ( ) s F s s s        1 L F s( )     1 1 2 ( ( )) s L F s L s s                             2 2 2 2 Res , lim lim st k k st st s s s se s s s se se s s s s s s                                           解：     2 2 ( ) t t t e e                   