电子科技大学：《数学物理方程与特殊函数 Mathematical Physics Equations with Special Function》课程教学资源（课件讲稿）第七章 Bessel函数 §7.4 Bessel函数应用

§7.4 Besselp函数应用 例设有半径为的薄圆盘，其侧面绝热，若圆盘边界上的温度恒保持为零度，且初 始温度为已知。求圆盘内的瞬时温度分布规律。 解： 2+ +R u(x,y,0)=p(x,y) u(x,y,t)=V(x,y)T(t) e+-R=0 Al址Bai约 Generalized T'=a2(VT+VnT） Bessel Functions of the First Kind V(c,y)+-gT0=0 u(x,y,0)=o(x,y)=p(pcose,psine)=f(p,0)

§7.4 Bessel函数应用 2 例 设有半径R为的薄圆盘，其侧面绝热，若圆盘边界上的温度恒保持为零度，且初 始温度为已知。求圆盘内的瞬时温度分布规律。 u x y t V x y T t ( , , ) ( , ) ( )  解：   2 2 2 2 2 2 2 2 2 2 2 , ( , ,0) , 0 x y R u u u a x y R t x y u x y x y u                                2 2 2 2 ( , ) ( ) 0 ( , ,0) ( , ) ( cos , sin ) ( , ) xx yy x y R VT a V T V T V x y T t u x y x y f                        

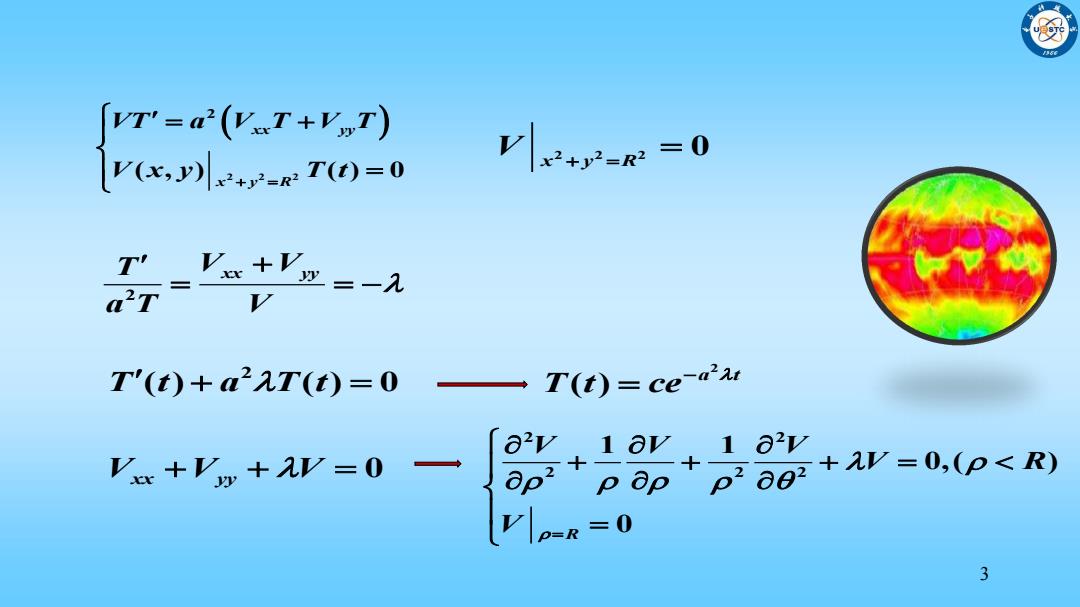
o V+-R=0 T'(t)+a2孔T(t)=0一 T(t)=ce-aa Vi +V+=0 +1 +pa8+r=0,(p<R) V=R=0 3

3 2 T V V xx yy a T V         2 2 2 2 ( , ) ( ) 0 xx yy x y R VT a V T V T V x y T t            2 T t a T t ( ) ( ) 0    2 2 2 0 x y R V    V V V xx yy     0 2 ( ) a t T t ce   2 2 2 2 2 1 1 0,( ) R 0 V V V V R V                         

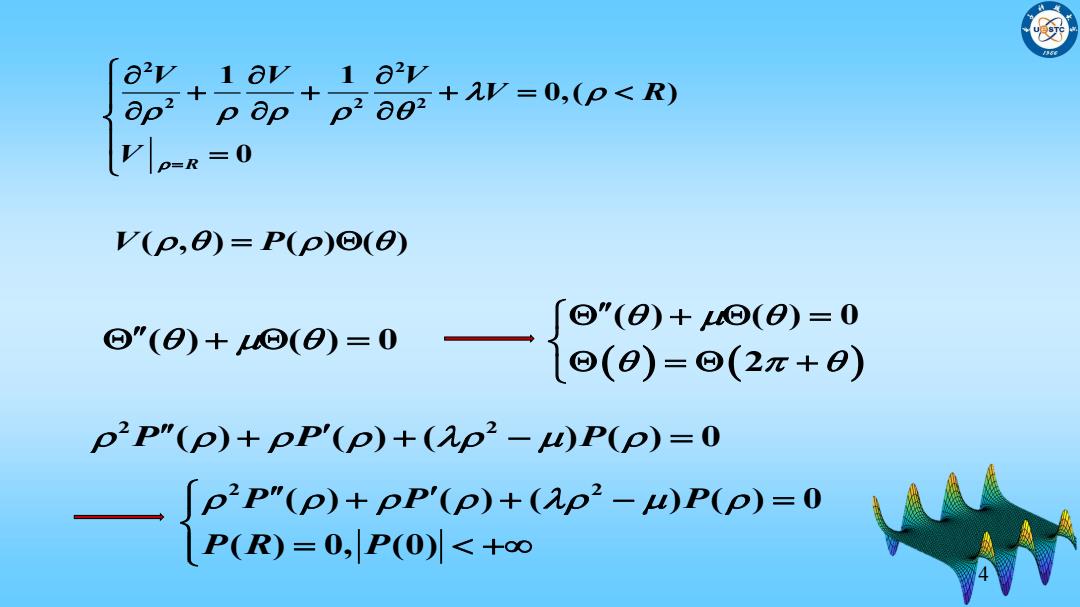
2/ E+P=0,(p<R) Ke-R=0 V(p,B)=P(p)⊙(B) oo+a0-0—8网89，l p2P"(p)+pP'(p)+(p2-)P(p)=0 —P6On-n-0

4 2 2 2 2 2 1 1 0,( ) R 0 V V V V R V                          V P ( , ) ( ) ( )           ( ) ( ) 0    2 2        P P P   ( ) ( ) ( ) ( ) 0         ( ) ( ) 0 2                  2 2 ( ) ( ) ( ) ( ) 0 ( ) 0, (0) P P P P R P                   

「⊙"(0)+⊙(0)=0 l⊙(0)=⊙(2x+8) hn=n2,n∈N ⊙，(0-2（为常数） 2 ()=a cosne+b'sin ne,n=1,2,... 5

5     ( ) ( ) 0 2                  2 , n   n n N 0 0 ( ) ( ) 2 ( ) cos sin , 1,2, n n n a a n b n n             为常数

RoR6n-o1-0 r=√夙p r2P"(r)+rP'(r)+(r2-n2)P( =0 P(r)=AJ (r)+BY (r) P(P)=AJ(Ap)+BY(Ap) Bessel Runctiors of the Rirst Kind 3. 0 limy (x)=-oo B=0 x→0 05

6 r    2 2 2 r P r rP r r n P r   ( ) ( ) ( ) ( ) 0     2 2 2 ( ) ( ) ( ) ( ) 0 ( ) 0, (0) P P n P P R P                   ( ) ( ) ( ) P r AJ r BY r   n n ( ) ( ) ( ) P AJ BY        n n 0 lim ( ) n x Y x    B  0

P(P)=AJ,(p) P(R)=AJn(√久R)=0 √久R=4wm,(m=1,2,…) 反=尽m=l.2,…无-（发）m=12weN R -1() umn=P(p)n()T(t) 7

7 ( ),( 1,2, ) n   R m   m ( ) ( ) n m P J mn n R           ( ) ( ) ( ) u P T t mn mn n mn     ( ) ( ) P AJ     n P R AJ R ( ) ( ) 0   n  ( ) , 1,2, n m m R     2 ( ) , 1,2, , n m m n m n N R           

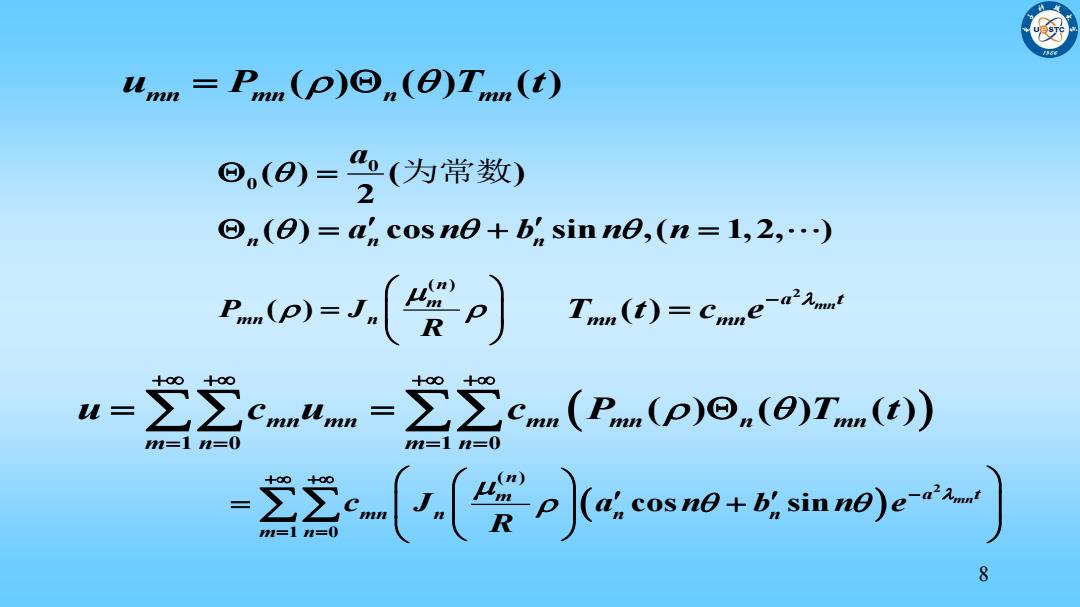
u=P(p)()T(t) ⊙(0)=（为常数） 2 ⊙n(0)=a'cos ne+b,sinn8,(n=1,2,…) o=(食p) Tn()）=Cme u=之∑cnm4n=之之cn.(D(p)o.(0Tn(t) n=1n=0 ==0 之交(（号小cmo+以nos 8

8 ( ) ( ) ( ) u P T t mn mn n mn     0 0 ( ) ( ) 2 ( ) cos sin ,( 1,2, ) n n n a a n b n n             为常数   1 0 1 0 ( ) ( ) ( ) mn mn mn mn n mn m n m n u c u c P T t                ( ) ( ) n m P J mn n R           2 ( ) a t mn T t c e mn mn      2 ( ) 1 0 cos sin m n n m a t mn n n n m n c J a n b n e R                          

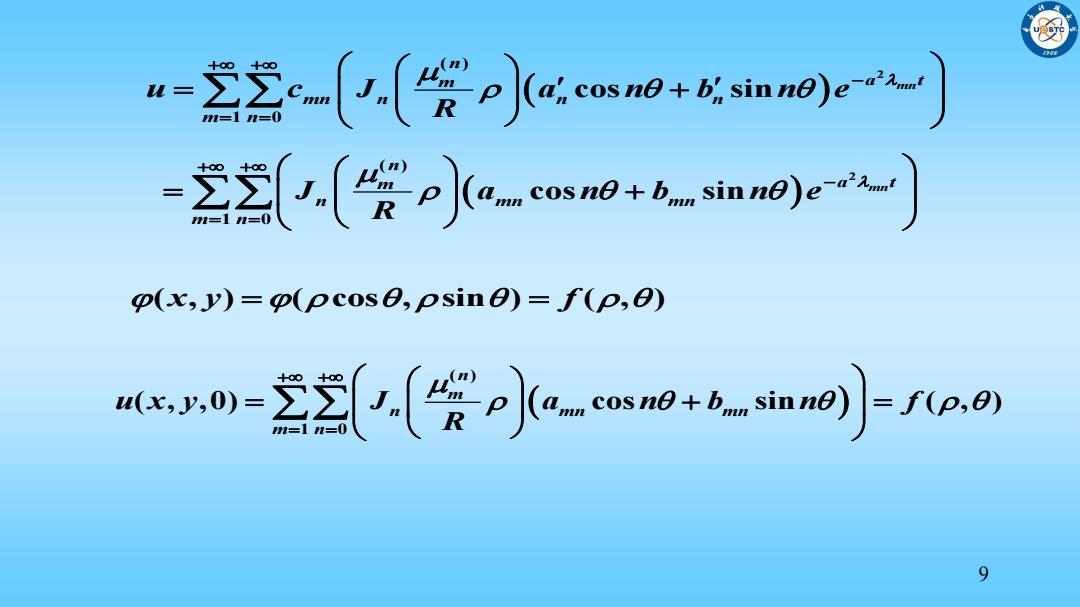
2-（一（发j水eow发no） u- 空（资pjao0+aino.） p(x,y)=o(pcose,psine)=f(p,0) -22((发小水小n0 9

9   2 ( ) 1 0 cos sin m n n m a t mn n n n m n u c J a n b n e R                             2 ( ) 1 0 cos sin m n n m a t n mn mn m n J a n b n e R                                 ( , ) ( cos , sin ) ( , ) x y f     ( ) 1 0 ( , ,0) cos sin ( , ) n m n mn mn m n u x y J a n b n f R                         

0-22(答Pja-w0+6no）小-a0 刚 =m(发p月 2((发小水e*6smo小（发Pj》-0 ∑(n cosn0+Bsin n8) 10

10   ( ) 1 0 ( , ,0) cos sin ( , ) n m n mn mn m n u x y J a n b n f R                            ( ) ( ) 1 0 ( ) cos sin , ( , ), : ( ) n n m k n mn mn n m n n n k k J a n b n J R R f J R g                                                 ( ) ( ) 0 0 cos sin ( ) cos si , n n n k k n kn k k kn kn n n n n g n J a n b n J R R n                                        

2.(gPj(oewn0+aino0)-空(ow0+Bno） k型 kn (gj-(紧n-空=y R2 a0-2芝(.（发pjao0+n0)-）

11     ) 0 0 2 ( cos sin cos sin n k n kn kn kn kn n n J a n b n n R     n                   2 2 ( ) ( ) , kn kn n n k n n kn k k n a b J J R R                     ( ) 2 2 2 2 2 ( ) ( ) 2 ( ) 1 1 0 d ( ) ( ) 2 2 n k n R m n n n n n m n m R R xJ x x R R J J J                          2 ( ) 1 0 ( , , ) cos sin m n n m a t n mn mn m n u t J a n b n e R                          