电子科技大学：《数学物理方程与特殊函数 Mathematical Physics Equations with Special Function》课程教学资源（课件讲稿）第六章 Green函数法 6.1 Green公式（1/2）

激学物理方程与特殊函激精品课程 第六章Green函数法 主讲：李明奇副教授

第六章 Green函数法 主讲：李明奇 副教授

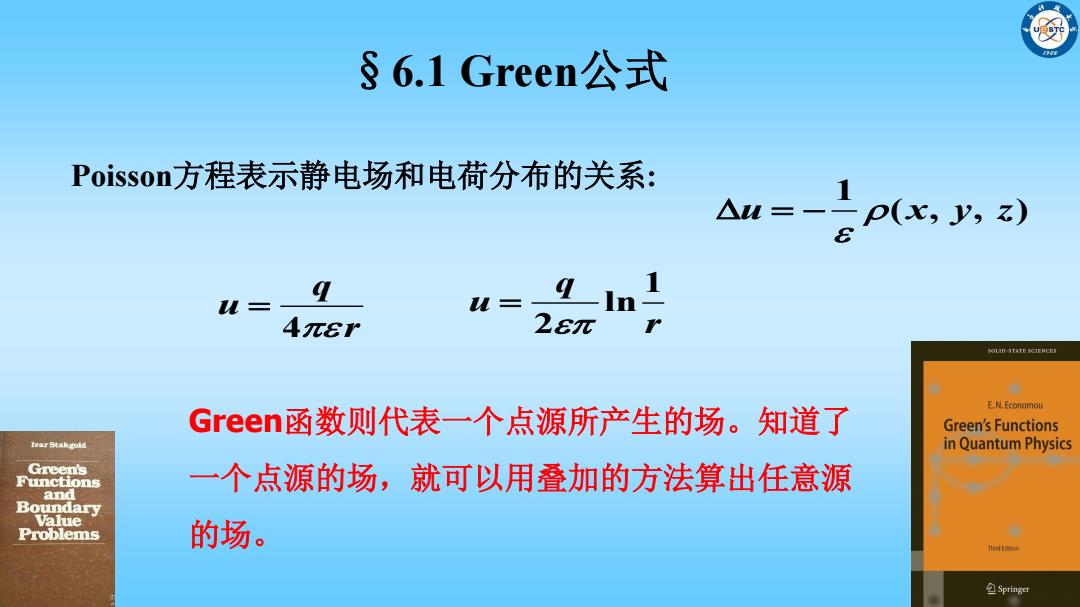
§6.1 Green公式 Poisson方程表示静电场和电荷分布的关系： 1 △=- p(x,y,z) u= u= 4元8r 2E元 SOLID-STATE ICIENCES E N.Economou Green函数则代表一个点源所产生的场。知道了 Green's Functions in Quantum Physics Green's Functions 一个点源的场，就可以用叠加的方法算出任意源 and Boundary Value Problems 的场。 hH时ii0 鱼Springer

§6.1 Green公式 2 Poisson方程表示静电场和电荷分布的关系: Green函数则代表一个点源所产生的场。知道了 一个点源的场，就可以用叠加的方法算出任意源 的场。 1 u x y z ( , , )     1 ln 2 q u  r  4 q u  r 

Dirichlet问题（第一类边值问题） △u=f(x,y,z),(x,y,Z)∈/ us=p(x,y,z) Neumann问题（第二类边值问题） △u=f(x,y,z),(x,y,z)∈V v.y.2 Robin问题（第三类边值问题） 「△u=f(x,y,z)(x,y,z)∈P 4小。=p(,w2,8别。=w(,y) (Victor)Gustave Robin: 1855-1897 3

3 Dirichlet问题（第一类边值问题） ( , , ), ( , , ) ( , , ) S u f x y z x y z V u x y z          Neumann问题（第二类边值问题） ( , , ), ( , , ) ( , , ) S u f x y z x y z V u x y z n          Robin问题（第三类边值问题） ( , , ), ( , , ) ( , , ), ( , , ) S S u f x y z x y z V u u x y z x y z n             

Gauss公式 ∯P4k+o+r=可JI(e.+g,+R)a =∯0，R-nio =∯P,L,Rd6 年i.6=∬vi,i=心0R

4   ( , , ) ( , , ) x y z S V S S Pdydz Qdzdx Rdxdy P Q R dV P Q R nd P Q R d                Gauss公式 , ( , , ) S V A d Adv A P Q R        

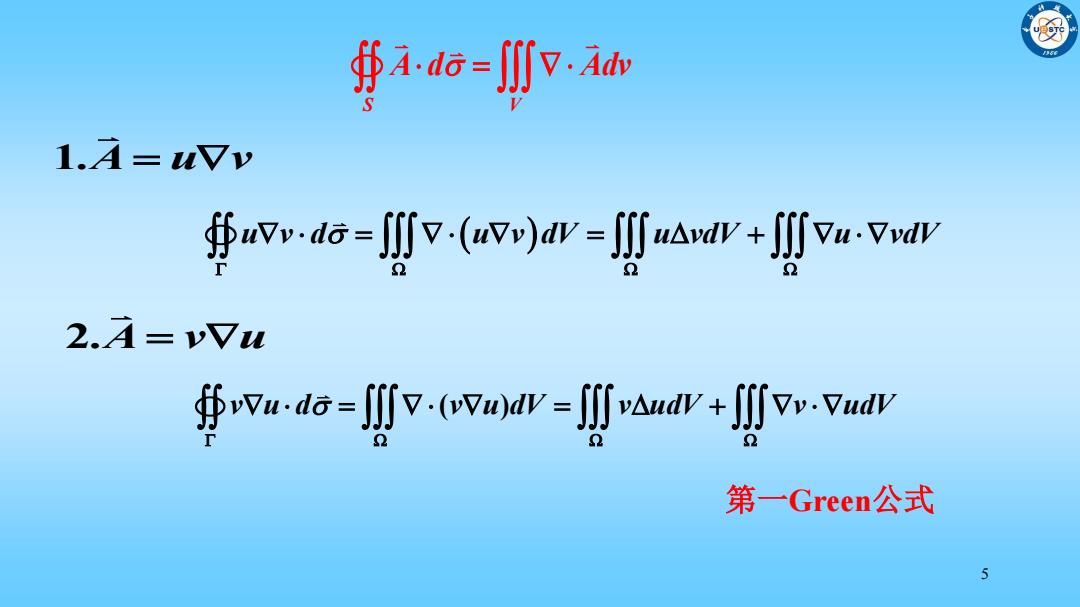
乎16=∬： 1.4=uVv ∯w-a6-∬-(wjav-∬uaar+∬u-vwW 2.4=vYu ∯wu-da=-(wmar=∬waw+∬p.vudv 第一Green公式 5

5 1.A u v   第一Green公式 u v d u v dV u vdV u vdV                        v u d v u dV v udV v udV  ( )                     2.A v u   S V A d Adv       

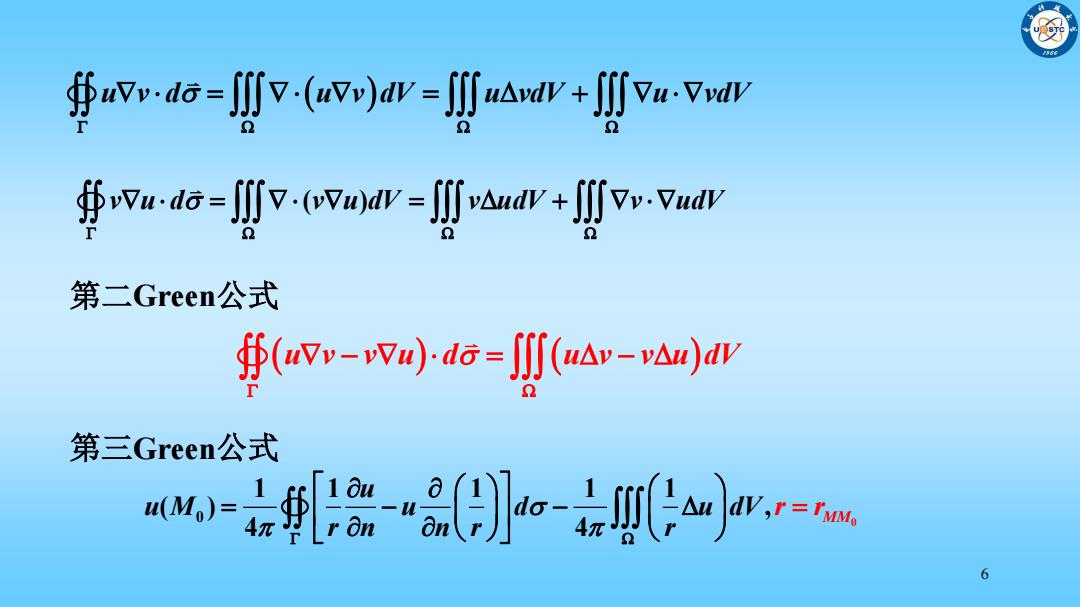
∯wv-i6-∬-(wjaw=∬ua+∬u-v ∯w,ia-∬-(owwW-项wav+∬m.van 第二Green公式 f(uv-wm)i6=aAr-）y 第三Green公式 -8-品ojrm

6 u v v u d u v v u dV                 第二Green公式 u v d u v dV u vdV u vdV                        v u d v u dV v udV v udV  ( )                     第三Green公式 0 0 1 1 1 1 1 ( ) , 4 4 MM u u M u d u dV r n n r r r  r                                 

第二Green公式 (wv-wu）iG-(av-an）W 第三Green公式 )-】如如m a()0 M Mo RT 7

7 u v v u d u v v u dV                 第二Green公式 第三Green公式 0 0 1 1 1 1 1 ( ) , 4 4 MM u u M u d u dV r n n r r r  r                                  0 1 M 0 r MM           z x O y   K M0 Ω Γ M

证明：令v(M=1/TMM, 球面「以M,为中心，为半径 ana太n]m 太n） -(）0-△w(ww M Mo 》 T 8

8 证明：令 0 ( ) 1 / MM v M r  球面Γε以 M0为中心，为ε半径 0 0 ( ) ) 1 ( 1 M K r r MM MM u M u M dV                        z x O y   K M0 Ω Γ M 0 0 1 ( ) 1 ( ) MM MM M u M d r n u M n r                           0 1 M 0 rMM           0 1 M M ( ) K MM u M dV r       0 0 1 1 ( ) ( ) M MM MM u M u M d n r r n                         

"品go="（0日o=∯÷o =京∯udo=4i-c四→4(M） ∮60do=4πe(u,)→0，(e→0) w-品 do+4xu(M) )-a-]a加-r-m 9

9 2 1 1 1 d u d u d n r r r r u                                  0  2 0 1 ud u u M 4 4            1 4 ( ) 0, 0 1 ( ) r u d d u u r n r                     0 1 1 1 4 ( ) u u dV u d u M r n r r n                                  0 0 1 1 1 1 1 ( ) , 4 4 MM u u M u d u dV r n n r r r  r                                 

品o-如n 定理若定解问题 △u=-f(x,y,z),(x,y,z)∈V us=o(.a小1s=w(xa） 的解存在，则 =石-会o+项np-m 10

10 0 1 1 1 1 1 ( ) 4 4 u u M u d u dV r n n r r                                  ( , , ),( , , ) ( , , ), ( , , ) S S u f x y z x y z V u u x y z x y z n               0 0 1 1 1 1 1 ( ) ( , , ) ( , , ) ( , , ) , 4 4 u M x y z x y z d f x y z dV MM r r r n r r                                  定理 若定解问题 的解存在，则