电子科技大学：《数学物理方程与特殊函数 Mathematical Physics Equations with Special Function》课程教学资源（课件讲稿）第四章 行波法（3/3）

激理方程与特殊函致 第四章行波法（三） 主讲：杨春

第四章 行波法(三) 主讲：杨春

本次课主要内容 一、二维波动方程柯西问题的降维法 二、行波法求解定解问题应用举例

本次课主要内容 一、二维波动方程柯西问题的降维法 二、行波法求解定解问题应用举例

一、二维波动方程柯西问题的降维法 求解：二维空间自由振动波动方程定解问题： u =a 02 (0) .)x. 求解方法：把二维看成三维的特殊情形，即把二维情形的方程、初始条件和波函数 看成与z无关的三维问题进行处理，从三维泊松公式出发，利用曲面积分计算，得到 二维问题的解。 三维泊松公式为： u(M,t)=

  2 2 2 2 2 2 2 0 0 , , , 0 ( , ) ( , ) t t u u u a x y t t x y u u x y x y t                                 ， 求解：二维空间自由振动波动方程定解问题： 求解方法：把二维看成三维的特殊情形，即把二维情形的方程、初始条件和波函数 看成与z无关的三维问题进行处理，从三维泊松公式出发，利用曲面积分计算，得到 二维问题的解。 一、二维波动方程柯西问题的降维法 三维泊松公式为： . . . . 2 1 ( ) ( ) ( , ) 4 M M S S at at M M u M t dS dS a t t t                   

a (M,t)= (M) 4πa 球面方程为： 5=z±Vat-(5-x)2-(m-y2 将初始条件代入泊松公式，且利用第一型曲面积分公式得到二维柯西问题计算公式： ux.y.t)= (5,) ddn 使用上，一般采用如下极坐标形式： x,y,)= Nar-r r-

球面方程为： 将初始条件代入泊松公式，且利用第一型曲面积分公式得到二维柯西问题计算公式: . . . . 2 1 ( ) ( ) ( , ) 4 M M at at S S M M u M t dS dS a t t t                    2 2 2 2          z a t x y ( ) ( ) 2 2 2 2 2 2 2 2 1 ( , ) 1 ( , ) ( , , ) + 2 2 D D ( ) ( ) ( ) ( ) u x y t d d d d a t a a t x y a t x y                                              使用上，一般采用如下极坐标形式： 2 2 0 0 0 0 2 2 2 2 2 2 1 ( cos , sin ) 1 ( cos , sin ) ( , , ) + 2 2 at at x r y r x r y r u x y t rdrd rdrd a t a a t r a t r                                     

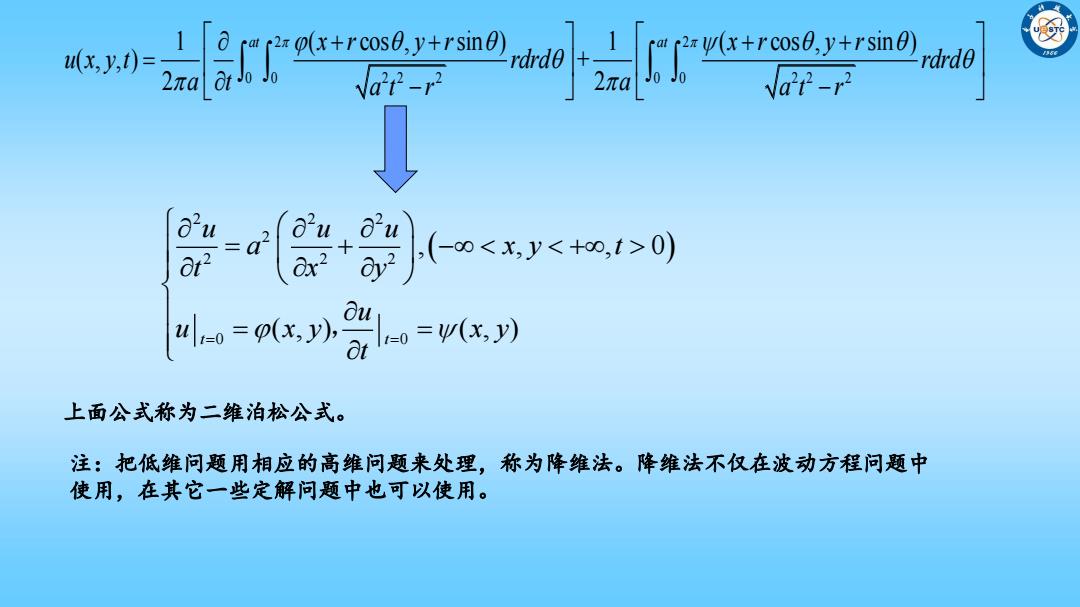
x,y,0= rdrd0 2πa NaP-r a2u d u +0(00) 4L=ox小=n 上面公式称为二维泊松公式。 注：把低维问题用相应的高维问题来处理，称为降维法。降维法不仅在波动方程问题中 使用，在其它一些定解问题中也可以使用

上面公式称为二维泊松公式。 2 2 0 0 0 0 2 2 2 2 2 2 1 ( cos , sin ) 1 ( cos , sin ) ( , , ) + 2 2 at at x r y r x r y r u x y t rdrd rdrd a t a a t r a t r                                        2 2 2 2 2 2 2 0 0 , , , 0 ( , ) ( , ) t t u u u a x y t t x y u u x y x y t                                 ， 注：把低维问题用相应的高维问题来处理，称为降维法。降维法不仅在波动方程问题中 使用，在其它一些定解问题中也可以使用

例1、用降维法由三维波动方程泊松公式推导出一维波动方程的达朗贝尔公式。 解：三维波动方程初值问题： u 2 =a 8t2 ,(-o00) 4le=xy,l=wy到 当u不依赖x,y时，即得到自由弦振动方程： or (0) 根据三维泊松公式： u(M,t)=

例1、用降维法由三维波动方程泊松公式推导出一维波动方程的达朗贝尔公式。 解：三维波动方程初值问题：   2 2 2 2 2 2 2 2 2 0 0 , , , , 0 ( , , ), ( , , ) t t u u u u a x y z t t x y z u u x y z x y z t                                    当u不依赖x, y时，即得到自由弦振动方程：   2 2 2 2 2 0 0 , 0 ( ), ( ) t t u u a z t t z u u z z t                        根据三维泊松公式： . . . . 2 1 ( ) ( ) ( , ) 4 M M S S at at M M u M t dS dS a t t t                   

(M,t)= (M)ds(M)ds Ana 当初始条件只与z相关时： 4w-》WFinnIJa rcos)(a)sin0d0 at 由定积分第二类换元法，令z+atC0SO=5,则： ∯2”s=2no5d5-…+ 同理可得到： ∯”s=2rjw0d5

当初始条件只与z相关时： 由定积分第二类换元法，令 ，则： . . . . 2 1 ( ) ( ) ( , ) 4 M M S S at at M M u M t dS dS a t t t                    . . 2 2 0 0 ( ) ( cos ) ( ) sin M S at M z at dS at d d t at               2 0 ( cos ) 2 ( ) sin z at at d at          z at   cos  . . ( ) 2 ( ) * M at z at z at S M dS d t            同理可得到： . . ( ) 2 ( ) ** M at z at z at S M dS d t           

(M,t)= pM'） Ana 将它们代入三维泊松公式得到： x0=a(r+am+pc-am+a∫E 注：通过降维法，一、二、三维自由振动柯西问题的求解公式均可以统一为泊松公式。 例2、求解定解问题： L-d aw=x+列0=0

将它们代入三维泊松公式得到： . . . . 2 1 ( ) ( ) ( , ) 4 M M S S at at M M u M t dS dS a t t t                    注：通过降维法，一、二、三维自由振动柯西问题的求解公式均可以统一为泊松公式。                x a t x a t d a u x t x at x at . 2 . 1 2 1 ( , )      例2、求解定解问题：   2 2 2 2 2 2 2 2 0 0 , , , 0 t t ( ), 0 u u u a x y t t x y u u x x y t                               

叫=+n =0 解：由二维泊松公式： 4x,y,)= 2πat0J0 a2-2 aP-P =x(x(x+rcos0,y+rsine)=(x+rcos0)(x+y+rcos@+rsine) =x2(x+y)+2x(x+y)rcos0+(x+y)r2 cos20+xr(sin@+cos0) +2xr2(sin0+cose)cos+r(sin0+cose)cos20

解：由二维泊松公式： 2 0 0 t t ( ), 0 u u x x y t        2 2 0 0 0 0 2 2 2 2 2 2 1 ( cos , sin ) 1 ( cos , sin ) ( , , ) + 2 2 at at x r y r x r y r u x y t rdrd rdrd a t a a t r a t r                                      2 0 0 2 2 2 1 ( cos , sin ) 2 at x r y r rdrd a t a t r                     2 0 ( ) u x x y t     2       x r y r x r x y r r        cos , sin ( cos ) ( cos sin ) 2 2 2 2 2 3 2 ( ) 2 ( ) cos ( ) cos (sin cos ) 2 (sin cos )cos (sin cos )cos x x y x x y r x y r x r xr r                      

由三函数的周期性、正交性、倍角公式得，cos日，Sin日，cos日Sin日，cos36,cos26 Sin日在0到2T上的积分均为零，而： 2π cos20d0=π 所以： 0rsin)d a'P-r2 =a+亮x德 2 =2x+x+y)ap uxyn-2a2arc+a+aex+nor=r+tar6x+0

由三函数的周期性、正交性、倍角公式得，cosθ,Sinθ, cosθ Sinθ, cos3θ, cos2θ Sinθ在0到2π上的积分均为零，而： 2 2 0 cos d       所以： 2 0 0 2 2 2 at ( cos , sin ) x r y r rdrd a t r           3 2 0 0 2 2 2 2 2 2 2 ( ) (3 ) at at rdr r dr x x y x y a t r a t r           2 3 3 2 2 ( ) (3 ) 3       x x y at x y a t 1 2 2 3 3 ( , , ) 2 ( ) (3 ) 2 3 u x y t x x y at x y a t a t                2 2 2     x x y a t x y ( ) (3 )