电子科技大学：《数值分析 Numerical Analysis》课程教学资源（课件讲稿）数值积分

数值积分 >数值积分基本概念 >插值型求积公式 >求积分的蒙特卡罗方法 >复合求积公式 >高斯型数值求积公式 >龙贝格外推计算公式

1 Ø数值积分基本概念 Ø插值型求积公式 Ø求积分的蒙特卡罗方法 Ø复合求积公式 Ø高斯型数值求积公式 Ø龙贝格外推计算公式 数值积分

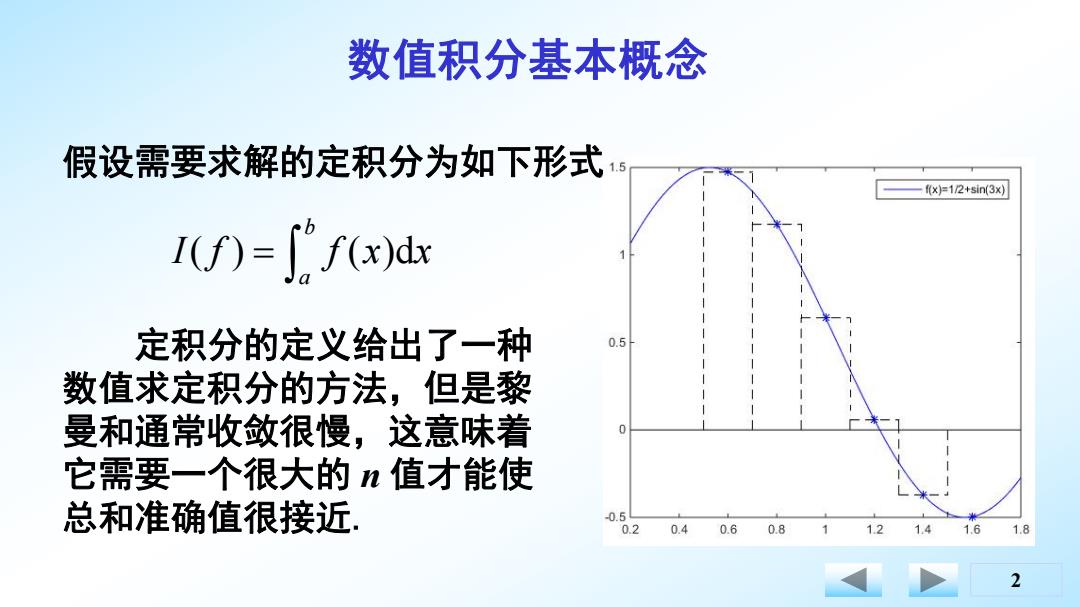
数值积分基本概念 假设需要求解的定积分为如下形式 5 f(x)=12+sin(3x) I(f)["f(x)dx 定积分的定义给出了一种 0.5 数值求定积分的方法，但是黎 曼和通常收敛很慢，这意味着 0 它需要一个很大的n值才能使 总和准确值很接近， -0.59 0.20.4 0.60.8 12 1.4

2 假设需要求解的定积分为如下形式： ( ) ( )d b a I f  f x x  定积分的定义给出了一种 数值求定积分的方法，但是黎 曼和通常收敛很慢，这意味着 它需要一个很大的 n 值才能使 总和准确值很接近. 数值积分基本概念

定积分与积分和式 假设需要求解的定积分为如下形式： If)=∫fx)dx 为了找到能够尽可能逼近()准确值的数值方法.通常，求 定积分近似值的形式为 I,(f)=∑wf(x) i=lo 3

3 定积分与积分和式 假设需要求解的定积分为如下形式： ( ) ( )d b a I f  f x x  为了找到能够尽可能逼近I(f)准确值的数值方法. 通常，求 定积分近似值的形式为   0 ( ) n n i i i i I f w f x   

数值求积公式的一般形式 ∫f(x)=∑Asf(x)+Rf1 k=0 RU 1— 数值求积公式余项 七09七1)…，七n— 求积结点 A,A1,…,An求积系数

4 数值求积公式的一般形式 ( ) ( ) [ ] 0 f x dx A f x R f n k k k b a      R[f ] —— 数值求积公式余项 x0 , x1 , ···, xn —— 求积结点 A0 , A1 , ···, An —— 求积系数

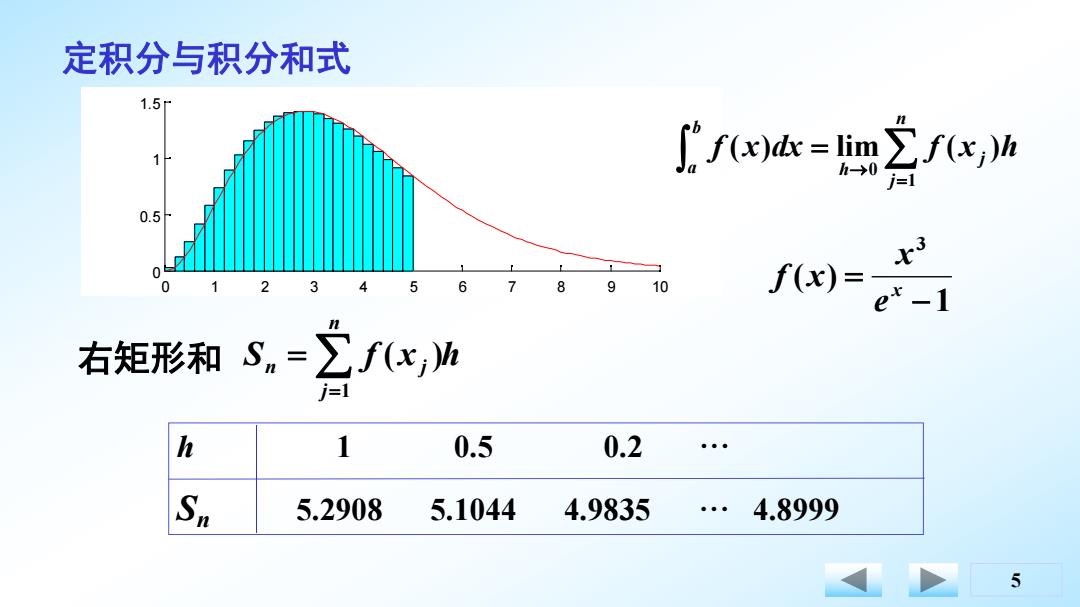
定积分与积分和式 1.5r f=2fc,h i= 0.5 x3 5 6 7 8 10 f(x)= e'-1 右矩形和S。=∑f(x,h i=1 h 1 0.5 0.2 Sn 5.2908 5.1044 4.9835 …4.8999 5

5 0 1 2 3 4 5 6 7 8 9 10 0 0.5 1 1.5 S f x h n j n  j   1 ( ) 定积分与积分和式     n j j h b a f x dx f x h 1 0 ( ) lim ( ) 右矩形和 h 1 0.5 0.2 ··· Sn 5.2908 5.1044 4.9835 ··· 4.8999 1 ( ) 3  x e x f x

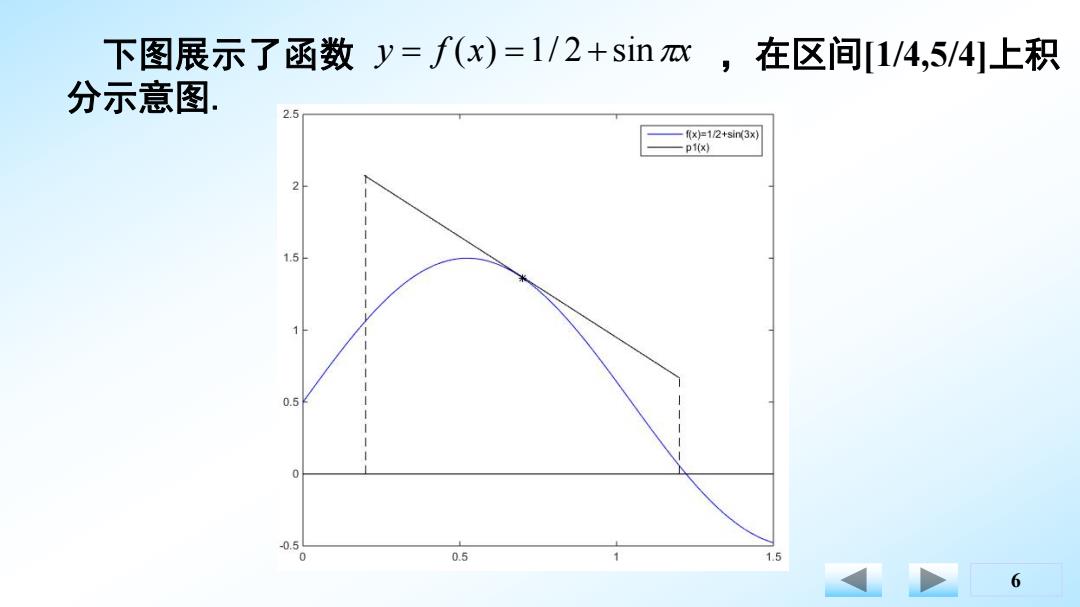
下图展示了函数y=f(x)=1/2+sinm, 在区间[1/4,5/41上积 分示意图 2.5 fx卢12+sin(3x) p1(x) 1.5 0.5 0 -0.5 0 0.5 1 1.5 6

6 下图展示了函数 ，在区间[1/4,5/4]上积 分示意图. y  f (x) 1/ 2  sinx

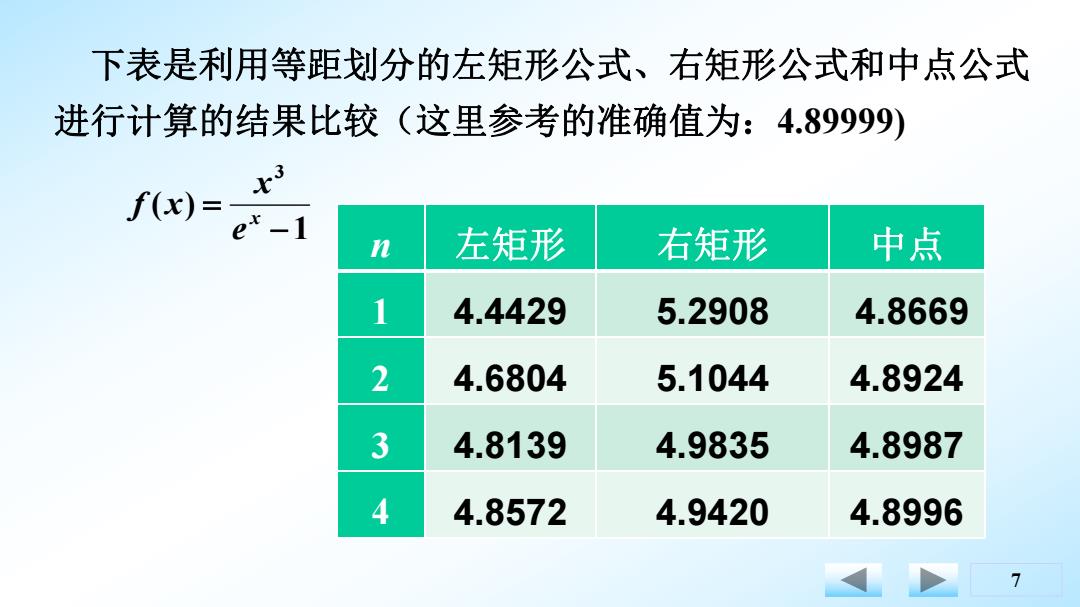
下表是利用等距划分的左矩形公式、右矩形公式和中点公式 进行计算的结果比较（这里参考的准确值为：4.89999) x3 f(x)= ex-I 左矩形 右矩形 中点 1 4.4429 5.2908 4.8669 2 4.6804 5.1044 4.8924 3 4.8139 4.9835 4.8987 4 4.8572 4.9420 4.8996 7

7 n 左矩形 右矩形 中点 1 4.4429 5.2908 4.8669 2 4.6804 5.1044 4.8924 3 4.8139 4.9835 4.8987 4 4.8572 4.9420 4.8996 1 ( ) 3  x e x f x 下表是利用等距划分的左矩形公式、右矩形公式和中点公式 进行计算的结果比较（这里参考的准确值为：4.89999)

插值型求积公式 对[a,b]做分划：≤x<X1<x2<…<x≤b Lagrange插值 f≈21，xx) fx)≈2心l,(ax)fx,) i=0 i=0 令A,=∫1，(x)c,(0j=01,2,… )∫f()≈∑A,f(x) 插值型求积公式的余项 1=-L-oea 8

8 对 [a，b]做分划: a≤ x0 < x1 < x2 < …… < xn≤b   n j j j f x l x f x 0 ( ) ( ) ( )      n j j b a j b a f x dx l x dx f x 0 ( ) [ ( ) ] ( ) 令 A l ( x)dx,( j 0,1,2, ,n) b a j   j       n j j j b a f x dx A f x 0 ( ) ( ) Lagrange 插值 插值型求积公式的余项         b a n n b a n x dx n f R f f x L x dx ( ) ( )! ( ) [ ] [ ( ) ( )] ( ) 1 1 1   插值型求积公式

例1.梯形公式 L(x)= yo 线型插值 x1-x0 x1-X0 L,(x)= -,l(x)= x-xo x1-x0 x1-xo 4-小8-0-04=08=2山-0 fea822@+fo】 梯形公式的误差（余项） R-(x-ms-y--as- 12 9

9 梯形公式的误差( 余项 ) ( ) 2 1 0 dx b a b a b x A b a       ( ) 2 1 1 dx b a b a x a A b a       ( ) [ f (a) f (b)] b a f x dx b a     2           b a b a x a x b dx f x a x b dx f R ( )( ) 2 ( ) ( )( ) 2 ( )  ( ) ( ) f  b a R     12 3 即  例1. 梯形公式 线型插值 1 0 0 1 1 0 1 0 ( ) , ( ) x x x x l x x x x x l x       0 1 0 1 1 1 0 0 ( ) y x x x x y x x x x L x       a b

1.5 x3 f(x)= -1 fx)≈48999 0.5 e g10 1.5 S.() 左矩形 梯形 右矩形 4.4429 4.8669 5.2908 5 4.6804 4.8924 5.1044 4.8139 4.8987 4.9835 4.8572 4.8996 4.9420 10

10 0 1 2 3 4 5 6 7 8 9 10 0 0.51 1.5 0 1 2 3 4 5 6 7 8 9 1 0 0 0.51 1.5 0 1 2 3 4 5 6 7 8 9 1 0 0 0.51 1.5 ( ) 4.8999 50   f x dx S f x f x h nj n  j j     1 1 [ ( ) ( )] 21 1 ( ) 3  x e x f x左矩形 梯形 右矩形 4.4429 4.8669 5.2908 4.6804 4.8924 5.1044 4.8139 4.8987 4.9835 4.8572 4.8996 4.9420